メネラウスの定理・チェヴァの定理
メネラウスの定理
定理《メネラウスの定理とその逆》
$3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ がそれぞれ $\triangle\mathrm{ABC}$ の $3$ 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の内分点または外分点であり,
そのうちの $2$ 個が内分点で $1$ 個が外分点, または $0$ 個が内分点で $3$ 個が外分点であるとする.
このとき, 次の $2$ つの条件は同値である.
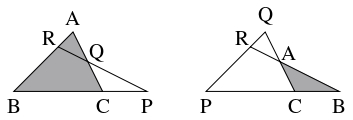
- (i)
- $3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ が同一直線上にある.
- (ii)
- $\dfrac{\mathrm{BP}}{\mathrm{PC}}\cdot\dfrac{\mathrm{CQ}}{\mathrm{QA}}\cdot\dfrac{\mathrm{AR}}{\mathrm{RB}} = 1$ が成り立つ.

証明
(i) を仮定して, (ii) を示す.
$6$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ が上図のような位置関係にあるとしても一般性を失わない.
このとき, 点 $\mathrm C$ を通って直線 $\mathrm{PQR}$ に平行な直線を引き, 辺 $\mathrm{AB}$ との交点を $\mathrm S$ とおくと,
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{BR}}{\mathrm{RS}}\cdot\frac{\mathrm{SR}}{\mathrm{RA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1\]
が得られる.
(ii) を仮定して, (i) を示す. このとき, $2$ 直線 $\mathrm{BC},$ $\mathrm{QR}$ の交点を $\mathrm P'$ とおくと, (i) $\Longrightarrow$ (ii) が成り立つことから \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1 = \frac{\mathrm{BP'}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}\] よって \[\frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\mathrm{BP'}}{\mathrm{PC}}\] が得られるので, $\mathrm P = \mathrm P'$ となる. ゆえに, $3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ は同一直線上にある.
(ii) を仮定して, (i) を示す. このとき, $2$ 直線 $\mathrm{BC},$ $\mathrm{QR}$ の交点を $\mathrm P'$ とおくと, (i) $\Longrightarrow$ (ii) が成り立つことから \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1 = \frac{\mathrm{BP'}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}\] よって \[\frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\mathrm{BP'}}{\mathrm{PC}}\] が得られるので, $\mathrm P = \mathrm P'$ となる. ゆえに, $3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ は同一直線上にある.
別証明
(i) を仮定して, (ii) を示す.
$6$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ が上図のような位置関係にあるとしても一般性を失わない.
このとき,
\[\frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\triangle\mathrm{BPQ}}{\triangle\mathrm{CPQ}}, \quad \frac{\mathrm{CQ}}{\mathrm{QA}} = \frac{\triangle\mathrm{CPQ}}{\triangle\mathrm{APQ}}, \quad \frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\triangle\mathrm{APQ}}{\triangle\mathrm{BPQ}}\]
であるから,
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\triangle\mathrm{BPQ}}{\triangle\mathrm{CPQ}}\cdot\frac{\triangle\mathrm{CPQ}}{\triangle\mathrm{APQ}}\cdot\frac{\triangle\mathrm{APQ}}{\triangle\mathrm{BPQ}} = 1\]
が成り立つ.
問題《デザルグの定理とその逆》
$\triangle\mathrm{ABC},$ $\triangle\mathrm A'\mathrm B'\mathrm C'$ について, $\mathrm{BC}$ と $\mathrm B'\mathrm C'$ の交点を $\mathrm P,$ $\mathrm{CA}$ と $\mathrm C'\mathrm A'$ の交点を $\mathrm Q,$ $\mathrm{AB}$ と $\mathrm A'\mathrm B'$ の交点を $\mathrm R$ とおく.
- (1)
- $3$ 本の直線 $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ が $1$ 点 $\mathrm O$ で交わるとする. このとき, $3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ は同一直線上にあることを示せ. (ヒント: $\triangle\mathrm{OBC}$ と直線 $\mathrm B'\mathrm C',$ $\cdots$ にメネラウスの定理を適用する.)
- (2)
- $3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ が同一直線上にあるとする. このとき, $3$ 本の直線 $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ は $1$ 点 $\mathrm O$ で交わることを示せ. (ヒント: $\triangle\mathrm{QAA}',$ $\triangle\mathrm{PBB}'$ に (1) の結果を適用する.)
解答例
- (1)
- $\triangle\mathrm{OBC}$ と直線 $\mathrm B'\mathrm C',$ $\triangle\mathrm{OCA}$ と直線 $\mathrm C'\mathrm A',$ $\triangle\mathrm{OAB}$ と直線 $\mathrm A'\mathrm B'$ にメネラウスの定理を適用すると,
\[\begin{aligned}
\frac{\mathrm O\mathrm B'}{\mathrm B'\mathrm B}\cdot\frac{\mathrm B\mathrm P}{\mathrm P\mathrm C}\cdot\frac{\mathrm C\mathrm C'}{\mathrm C'\mathrm O} &= 1, \\
\frac{\mathrm O\mathrm C'}{\mathrm C'\mathrm C}\cdot\frac{\mathrm C\mathrm Q}{\mathrm Q\mathrm A}\cdot\frac{\mathrm A\mathrm A'}{\mathrm A'\mathrm O} &= 1, \\
\frac{\mathrm O\mathrm A'}{\mathrm A'\mathrm A}\cdot\frac{\mathrm A\mathrm R}{\mathrm R\mathrm B}\cdot\frac{\mathrm B\mathrm B'}{\mathrm B'\mathrm O} &= 1
\end{aligned}\]
が得られる.
辺々を掛け合わせると
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1\]
が得られるから, メネラウスの定理の逆により $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ は同一直線上にある.
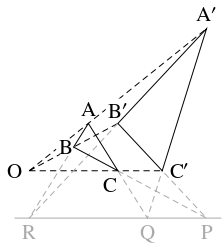
- (2)
- $2$ 直線 $\mathrm{AA}',$ $\mathrm{BB}'$ の交点を $\mathrm O$ とおく. $3$ 点 $\mathrm O,$ $\mathrm C,$ $\mathrm C'$ が同一直線上にあることを示せばよい. $\triangle\mathrm{QAA}',$ $\triangle\mathrm{PBB}'$ において, $\mathrm{QP},$ $\mathrm{AB},$ $\mathrm A'\mathrm B'$ は $1$ 点 $\mathrm R$ で交わるから, (1) の結果により, $\mathrm{AA}'$ と $\mathrm{BB}'$ の交点 $\mathrm O,$ $\mathrm{AQ}$ と $\mathrm{BP}$ の交点 $\mathrm C,$ $\mathrm{QA}'$ と $\mathrm{PB}'$ の交点 $\mathrm C'$ は同一直線上にある. ゆえに, $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ は $1$ 点 $\mathrm O$ で交わる.
参考
- 本問の結果は,「デザルグの定理」(Desargues's theorem) と呼ばれ,「射影幾何学」(projective geometry) の最も基本的な定理の $1$ つである.
- 定理の主張において点と直線をすべて入れ替える (“$1$ 点で交わる” と “$1$ 直線上にある” も入れ替える) ことで得られる定理をもとの定理の「双対」(dual) と呼ぶ. 「デザルグの定理」は,「双対」が「デザルグの定理」自身であるという意味で,「自己双対的」である.
- 「複比」を使う証明もある.
問題《完全四辺形に関するニュートンの定理》
四角形 $\mathrm{ABCD}$ において,
向かい合う $2$ 辺 $\mathrm{AB},$ $\mathrm{CD}$ の延長が点 $\mathrm E$ で交わり,
向かい合う $2$ 辺 $\mathrm{AD},$ $\mathrm{BC}$ の延長が点 $\mathrm F$ で交わるとする.
線分 $\mathrm{AC},$ $\mathrm{BD},$ $\mathrm{EF}$ の中点をそれぞれ $\mathrm L,$ $\mathrm M,$ $\mathrm N$ とおく.
- (1)
- 線分 $\mathrm{CB},$ $\mathrm{BE},$ $\mathrm{EC}$ の中点をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおく. $\mathrm{EA},$ $\mathrm{AB},$ $\mathrm{BF},$ $\mathrm{FC},$ $\mathrm{CD},$ $\mathrm{DE}$ を用いて 比 $\dfrac{\mathrm{RL}}{\mathrm{LP}},$ $\dfrac{\mathrm{PM}}{\mathrm{MQ}},$ $\dfrac{\mathrm{QN}}{\mathrm{NR}}$ を表せ.
- (2)
- $3$ 点 $\mathrm L,$ $\mathrm M,$ $\mathrm N$ は同一直線上にあることを示せ.
解答例
- (1)
- $\triangle\mathrm{CAE},$ $\triangle\mathrm{CAB}$ に中点連結定理を適用すると \[\mathrm{RL} = \frac{1}{2}\mathrm{EA}, \quad \mathrm{LP} = \frac{1}{2}\mathrm{AB}\] となるから, \[\frac{\mathrm{RL}}{\mathrm{LP}} = \frac{\mathrm{EA}}{\mathrm{AB}} \quad \cdots [1]\] が成り立つ. 同様に, \[\begin{aligned} \frac{\mathrm{PM}}{\mathrm{MQ}} &= \frac{\mathrm{CD}}{\mathrm{DE}} \quad \cdots [2], \\ \frac{\mathrm{QN}}{\mathrm{NR}} &= \frac{\mathrm{BF}}{\mathrm{FC}} \quad \cdots [3] \end{aligned}\] である.
- (2)
- $[1]$~$[3]$ の辺々を掛け合わせると, メネラウスの定理により \[\begin{aligned} &\frac{\mathrm{RL}}{\mathrm{LP}}\cdot\frac{\mathrm{PM}}{\mathrm{MQ}}\cdot\frac{\mathrm{QN}}{\mathrm{NR}} = \frac{\mathrm{EA}}{\mathrm{AB}}\cdot\frac{\mathrm{CD}}{\mathrm{DE}}\cdot\frac{\mathrm{BF}}{\mathrm{FC}} \\ &= \frac{\mathrm{EA}}{\mathrm{AB}}\cdot\frac{\mathrm{BF}}{\mathrm{FC}}\cdot\frac{\mathrm{CD}}{\mathrm{DE}} = 1 \end{aligned}\] となる. よって, メネラウスの定理の逆により, $3$ 点 $\mathrm L,$ $\mathrm M,$ $\mathrm N$ は同一直線上にある.
参考
- $4$ 直線とそれらの交点である $6$ 点からなる図形を「完全四辺形」(complete quadrilateral) と呼ぶ.
- 本問の結果は「完全四辺形」に関する「ニュートンの定理」(Newton's theorem) として知られている. 別証明については, こちらを参照されたい.
- 平行四辺形でない四角形において, 対角線の中点を結ぶ直線を「ニュートン線」(Newton line) と呼ぶ.
- 向かい合う辺の中点を結ぶ直線の交点は「ニュートン線」上にあることも知られている.
チェヴァの定理
定理《チェヴァの定理とその逆》
$3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ がそれぞれ $\triangle\mathrm{ABC}$ の $3$ 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の内分点または外分点であり,
そのうちの $3$ 個が内分点で $0$ 個が外分点, または $1$ 個が内分点で $2$ 個が外分点であるとする.
このとき, 次の $2$ つの条件は同値である.
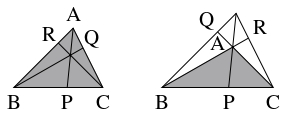
- (i)
- $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点で交わるか, すべて平行である.
- (ii)
- $\dfrac{\mathrm{BP}}{\mathrm{PC}}\cdot\dfrac{\mathrm{CQ}}{\mathrm{QA}}\cdot\dfrac{\mathrm{AR}}{\mathrm{RB}} = 1$ が成り立つ.

証明
(i) を仮定して, (ii) を示す.
(ii) を仮定して, (i) を示す. 点 $\mathrm P$ が辺 $\mathrm{BC}$ 上にあるとしても一般性を失わないから, その場合を考える. $2$ 直線 $\mathrm{BQ},$ $\mathrm{CR}$ が平行でないとして, $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点で交わることを示せばよい. $2$ 直線 $\mathrm{BQ},$ $\mathrm{CR}$ の交点を $\mathrm O$ とおき, 直線 $\mathrm{AO}$ と辺 $\mathrm{BC}$ の交点を $\mathrm P'$ とおくと, (i) $\Longrightarrow$ (ii) が成り立つことから \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1 = \frac{\mathrm{BP'}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}\] よって \[\frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\mathrm{BP'}}{\mathrm{PC}}\] が得られるので, $\mathrm P = \mathrm P'$ となる. ゆえに, $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ は $1$ 点で交わる.
- $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点 $\mathrm O$ で交わるとき. $\triangle\mathrm{ABP}$ と直線 $\mathrm{BQ},$ および $\triangle\mathrm{ACP}$ と直線 $\mathrm{CR}$ にそれぞれメネラウスの定理を適用すると, \[\begin{aligned} \frac{\mathrm{BC}}{\mathrm{CP}}\cdot\frac{\mathrm{PO}}{\mathrm{OA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} &= 1 \quad \cdots [1], \\ \frac{\mathrm{CB}}{\mathrm{BP}}\cdot\frac{\mathrm{PO}}{\mathrm{OA}}\cdot\frac{\mathrm{AQ}}{\mathrm{QC}} &= 1 \quad \cdots [2] \end{aligned}\] となる. $[1]\div [2]$ から, \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1\] が得られる.
- $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ がすべて平行であるとき. \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{BA}}{\mathrm{AR}}\cdot\frac{\mathrm{BC}}{\mathrm{BP}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{BA}}{\mathrm{BR}}\cdot\frac{\mathrm{BC}}{\mathrm{BP}} = 1\] が成り立つ.
(ii) を仮定して, (i) を示す. 点 $\mathrm P$ が辺 $\mathrm{BC}$ 上にあるとしても一般性を失わないから, その場合を考える. $2$ 直線 $\mathrm{BQ},$ $\mathrm{CR}$ が平行でないとして, $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点で交わることを示せばよい. $2$ 直線 $\mathrm{BQ},$ $\mathrm{CR}$ の交点を $\mathrm O$ とおき, 直線 $\mathrm{AO}$ と辺 $\mathrm{BC}$ の交点を $\mathrm P'$ とおくと, (i) $\Longrightarrow$ (ii) が成り立つことから \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1 = \frac{\mathrm{BP'}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}\] よって \[\frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\mathrm{BP'}}{\mathrm{PC}}\] が得られるので, $\mathrm P = \mathrm P'$ となる. ゆえに, $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ は $1$ 点で交わる.
別証明
(i) を仮定して, (ii) を示す.
- $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点 $\mathrm O$ で交わるとき. \[\frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\triangle\mathrm{OAB}}{\triangle\mathrm{OCA}}, \quad \frac{\mathrm{CQ}}{\mathrm{QA}} = \frac{\triangle\mathrm{OBC}}{\triangle\mathrm{OAB}}, \quad \frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\triangle\mathrm{OCA}}{\triangle\mathrm{OBC}}\] であるから, \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\triangle\mathrm{OAB}}{\triangle\mathrm{OCA}}\cdot\frac{\triangle\mathrm{OBC}}{\triangle\mathrm{OAB}}\cdot\frac{\triangle\mathrm{OCA}}{\triangle\mathrm{OBC}} = 1\] が成り立つ.
- $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ がすべて平行であるとき. 上記と同様.
問題《三角形の五心》
次のことを示せ.
- (A)
- $\triangle\mathrm{ABC}$ の $3$ 頂点と対辺の中点を結ぶ直線は $1$ 点で交わる.
- (B1)
- $\triangle\mathrm{ABC}$ の $3$ 頂点から対辺に下ろした垂線は $1$ 点で交わる.
- (B2)
- $\triangle\mathrm{ABC}$ の $3$ 辺の垂直二等分線は $1$ 点で交わる.
- (C)
- $\triangle\mathrm{ABC}$ の $3$ つの内角の二等分線は $1$ 点で交わる.
- (D)
- $\triangle\mathrm{ABC}$ の $1$ つの内角の二等分線と他の $2$ つの外角の二等分線は $1$ 点で交わる. ただし, 外角の二等分線は対辺と平行でないとする.
解答例
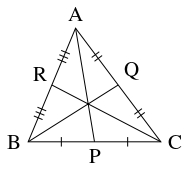
- (A)
- 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の中点をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおくと,
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\dfrac{\mathrm{BC}}{2}}{\dfrac{\mathrm{BC}}{2}}\cdot\frac{\dfrac{\mathrm{CA}}{2}}{\dfrac{\mathrm{CA}}{2}}\cdot\frac{\dfrac{\mathrm{AB}}{2}}{\dfrac{\mathrm{AB}}{2}} = 1\]
となるから, チェヴァの定理の逆により直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ は $1$ 点で交わる.
- (B1)
- (i)
- $\triangle\mathrm{ABC}$ が直角三角形のとき. $3$ 本の垂線は,直角の頂点で交わる.
- (ii)
- $\triangle\mathrm{ABC}$ が直角三角形でないとき.
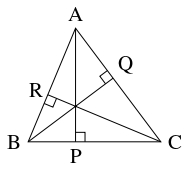
頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ から直線 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ に下ろした垂線の足を $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおく.
このとき, $\triangle\mathrm{ABQ}$ と $\triangle\mathrm{ACR}$ は相似であるから, $\dfrac{\mathrm{AR}}{\mathrm{AQ}} = \dfrac{\mathrm{AC}}{\mathrm{AB}}$ が成り立つ.
同様に $\dfrac{\mathrm{BP}}{\mathrm{BR}} = \dfrac{\mathrm{BA}}{\mathrm{BC}},$ $\dfrac{\mathrm{CQ}}{\mathrm{CP}} = \dfrac{\mathrm{CB}}{\mathrm{CA}}$ であるから,
\[\begin{aligned}
\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} &= \frac{\mathrm{AR}}{\mathrm{AQ}}\cdot\frac{\mathrm{BP}}{\mathrm{BR}}\cdot\frac{\mathrm{CQ}}{\mathrm{CP}} \\
&= \frac{\mathrm{AC}}{\mathrm{AB}}\cdot\frac{\mathrm{BA}}{\mathrm{BC}}\cdot\frac{\mathrm{CB}}{\mathrm{CA}} = 1
\end{aligned}\]
が成り立つ.
よって, チェヴァの定理の逆により, 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ は $1$ 点で交わる.
- (B2)
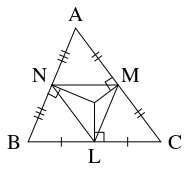
- $\triangle\mathrm{ABC}$ において, 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の中点を $\mathrm L,$ $\mathrm M,$ $\mathrm N$ とおく.
中点連結定理により $\mathrm{BC}$ と $\mathrm{MN},$ $\mathrm{CA}$ と $\mathrm{NL},$ $\mathrm{AB}$ と $\mathrm{LM}$ は平行であるから,
辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の垂直二等分線は $\triangle\mathrm{LMN}$ の頂点 $\mathrm L,$ $\mathrm M,$ $\mathrm N$ から対辺に下ろした垂線と一致する.
よって, (B1) により $\triangle\mathrm{ABC}$ の $3$ 辺の垂直二等分線は $1$ 点で交わる.
- (C)
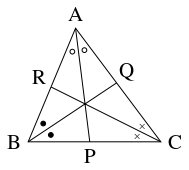
- $\triangle\mathrm{ABC}$ において, $\angle\mathrm A,$ $\angle\mathrm B,$ $\angle\mathrm C$ の内角の二等分線と辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の交点をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおくと,
\[\frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\mathrm{AB}}{\mathrm{CA}}, \quad \frac{\mathrm{CQ}}{\mathrm{QA}} = \frac{\mathrm{BC}}{\mathrm{AB}}, \quad \frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{CA}}{\mathrm{BC}}\]
となり,
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{AB}}{\mathrm{CA}}\cdot\frac{\mathrm{BC}}{\mathrm{AB}}\cdot\frac{\mathrm{CA}}{\mathrm{BC}} = 1\]
となるから, チェヴァの定理の逆により直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ は $1$ 点で交わる.
- (D)
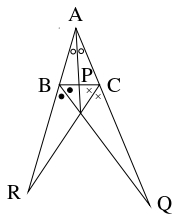
- $\triangle\mathrm{ABC}$ において, $\angle\mathrm A$ の内角, $\angle\mathrm B$ の外角, $\angle\mathrm C$ の外角の二等分線と辺 $\mathrm{BC},$ $\mathrm{CA}$ の延長, $\mathrm{AB}$ の延長の交点をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおくと,
\[\frac{\mathrm{BP}}{\mathrm{PC}} = \frac{\mathrm{AB}}{\mathrm{CA}}, \quad \frac{\mathrm{CQ}}{\mathrm{QA}} = \frac{\mathrm{BC}}{\mathrm{AB}}, \quad \frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{CA}}{\mathrm{BC}}\]
となり,
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{AB}}{\mathrm{CA}}\cdot\frac{\mathrm{BC}}{\mathrm{AB}}\cdot\frac{\mathrm{CA}}{\mathrm{BC}} = 1\]
となるから, チェヴァの定理の逆により直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ は $1$ 点で交わる.
参考
- (A) の交点を $\triangle\mathrm{ABC}$ の重心(center of gravity) と呼ぶ.
- (B1) の交点を $\triangle\mathrm{ABC}$ の垂心(orthocenter) と呼ぶ (座標を使った証明についてはこちらを参照).
- (B2) の交点を $\triangle\mathrm{ABC}$ の外心(circumcenter) と呼ぶ. $\triangle\mathrm{ABC}$ の $3$ 頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ を通る円周の中心は外心である. この円を $\triangle\mathrm{ABC}$ の外接円(circumscribed circle) と呼ぶ.
- (C) の交点を $\triangle\mathrm{ABC}$ の内心(inner center) と呼ぶ. $\triangle\mathrm{ABC}$ の $3$ 辺に接する円の中心は内心である. この円を $\triangle\mathrm{ABC}$ の内接円(inscribed circle) と呼ぶ.
- (D) の交点を $\triangle\mathrm{ABC}$ の $\angle\mathrm A$ 内の「傍心」(excenter) と呼ぶ. $\triangle\mathrm{ABC}$ の辺 $\mathrm{BC}$ と $\mathrm{AB}$ の延長, $\mathrm{AC}$ の延長に接する円の中心は $\angle\mathrm A$ 内の「傍心」である. この円を $\triangle\mathrm{ABC}$ の $\angle\mathrm A$ 内の「傍接円」(escribed circle) と呼ぶ. なお,「傍接円」は, 外角の二等分線が対辺と平行な場合にも存在する.
問題《三角形のジェルゴンヌ点とナーゲル点》
次のことを示せ.
- (A)
- $\triangle\mathrm{ABC}$ の $3$ 頂点と対辺における内接円の接点を結ぶ直線は $1$ 点で交わる.
- (B)
- (1)
- $\triangle\mathrm{ABC}$ の各頂点からその角内の傍接円に引いた接線の長さは $\triangle\mathrm{ABC}$ の周の長さの半分である.
- (2)
- $\triangle\mathrm{ABC}$ の $3$ 頂点と対辺における傍接円の接点を結ぶ直線は $1$ 点で交わる.
解答例
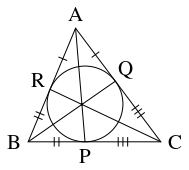
- (A)
- $\triangle\mathrm{ABC}$ において, 内接円と辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の接点をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおくと,
\[\mathrm{BP} = \mathrm{RB}, \quad \mathrm{CQ} = \mathrm{PC}, \quad \mathrm{AR} = \mathrm{QA}\]
から
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{BP}}{\mathrm{RB}}\cdot\frac{\mathrm{CQ}}{\mathrm{PC}}\cdot\frac{\mathrm{AR}}{\mathrm{QA}} = 1\]
となるので, チェヴァの定理の逆により直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ は $1$ 点で交わる.
- (B)
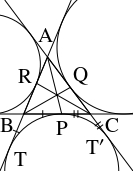
- $\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $s = \dfrac{a+b+c}{2}$ とおく.
また, 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ における傍接円の接点をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおく.
さらに, $\angle\mathrm A$ 内の傍接円と辺 $\mathrm{AB}$ の延長, $\mathrm{AC}$ の延長の接点をそれぞれ $\mathrm T,$ $\mathrm T'$ とおく.
- (1)
- \[\begin{aligned} \mathrm{AT} &= \mathrm{AB}+\mathrm{BT} = c+\mathrm{BP} \\ &= c+\mathrm{BC}-\mathrm{PC} = c+a-\mathrm{CT}' \\ &= c+a-(\mathrm{AT}'-\mathrm{AC}) \\ &= c+a+b-\mathrm{AT}, \\ 2\mathrm{AT} &= a+b+c \end{aligned}\] から \[\mathrm{AT} = \frac{a+b+c}{2} = s\] が得られる. よって, $\triangle\mathrm{ABC}$ の頂点から傍接円に引いた接線の長さはいずれも $\triangle\mathrm{ABC}$ の周の長さの半分である.
- (2)
- (1) により,
\[\mathrm{BP} = \mathrm{BT} = \mathrm{AT}-\mathrm{AB} = s-c\]
が成り立つ.
同様に
\[\begin{aligned}
\mathrm{QA} &= s-c, \\
\mathrm{CQ} &= \mathrm{RB} = s-a, \\
\mathrm{AR} &= \mathrm{PC} = s-b
\end{aligned}\]
が成り立つ.
よって,
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{\mathrm{BP}}{\mathrm{QA}}\cdot\frac{\mathrm{CQ}}{\mathrm{RB}}\cdot\frac{\mathrm{AR}}{\mathrm{PC}} = 1\]
であるから, チェヴァの定理の逆により直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ は $1$ 点で交わる.
参考
- (A) の交点を $\triangle\mathrm{ABC}$ の「ジェルゴンヌ点」(Gergonne point) と呼ぶ.
- (B) の交点を $\triangle\mathrm{ABC}$ の「ナーゲル点」(Nagel point) と呼ぶ.
- これら $2$ 点は互いに「等長共役点」の関係にある (次問を参照).
- 正三角形でない三角形において,「オイラー線」(外心 $\mathrm O,$ 重心 $\mathrm G,$ 垂心 $\mathrm H$ をこの順に通る直線) と, 内心と「ジェルゴンヌ点」を結ぶ直線との交点は, 外心に対して垂心と対称な位置にある. この点を「ド・ロンシャン点」(de Longchamps Point) と呼ぶ.
- 正三角形でない三角形において, 内心 $\mathrm I,$ 重心 $\mathrm G,$「ナーゲル点」$\mathrm N$ はこの順に $1$ 直線上にある. この直線を「ナーゲル線」(Nagel line) と呼ぶ. $\mathrm{IG}:\mathrm{GN} = 1:2$ であることが知られている ($\mathrm{OG}:\mathrm{GH} = 1:2$ の類似).
問題《三角形に関する等長共役点》
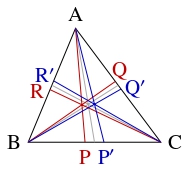
$\triangle\mathrm{ABC}$ の辺 $\mathrm{BC}$ 上に点 $\mathrm P,$ $\mathrm P',$ 辺 $\mathrm{CA}$ 上に点 $\mathrm Q,$ $\mathrm Q',$ 辺 $\mathrm{AB}$ 上に $\mathrm R,$ $\mathrm R'$ があり,
\[\mathrm{BP} = \mathrm{CP}', \quad \mathrm{CQ} = \mathrm{AQ}', \quad \mathrm{AR} = \mathrm{BR}'\]
を満たし, $3$ 本の直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点で交わるとする.
このとき, $3$ 本の直線 $\mathrm{AP}',$ $\mathrm{BQ}',$ $\mathrm{CR}'$ も $1$ 点で交わることを示せ.

解答例
$3$ 本の直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点で交わるとき, チェヴァの定理により
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1\]
が成り立ち, これと仮定, および
\[\begin{aligned}
\mathrm{BP}' &= \mathrm{BC}-\mathrm{CP}' = \mathrm{BC}-\mathrm{BP} = \mathrm{CP}, \\
\mathrm{CQ}' &= \mathrm{CA}-\mathrm{AQ}' = \mathrm{CA}-\mathrm{CQ} = \mathrm{AQ}, \\
\mathrm{AR}' &= \mathrm{AB}-\mathrm{BR}' = \mathrm{AB}-\mathrm{AR} = \mathrm{BR}
\end{aligned}\]
により
\[\frac{\mathrm{BP}'}{\mathrm P'\mathrm C}\cdot\frac{\mathrm{CQ}'}{\mathrm Q'\mathrm A}\cdot\frac{\mathrm{AR}'}{\mathrm R'\mathrm B} = \frac{\mathrm{CP}}{\mathrm{PB}}\cdot\frac{\mathrm{AQ}}{\mathrm{QC}}\cdot\frac{\mathrm{BR}}{\mathrm{RA}} = 1\]
が成り立つから, チェヴァの定理の逆により $3$ 本の直線 $\mathrm{AP}',$ $\mathrm{BQ}',$ $\mathrm{CR}'$ も $1$ 点で交わる.
参考
- 線分 $\mathrm{XY}$ の中点 $\mathrm M,$ 線分 $\mathrm{XY}$ 上の点 $\mathrm P,$ $\mathrm P'$ に対して $3$ つの条件
は同値である.(i) $\mathrm{MP} = \mathrm{MP}'$ (ii) $\mathrm{XP} = \mathrm{YP}'$ (iii) $\mathrm{YP} = \mathrm{XP}'$ - 本問において, $3$ 本の直線 $\mathrm{AP}',$ $\mathrm{BQ}',$ $\mathrm{CR}'$ の交点を $3$ 本の直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ の交点の「等長共役点」(isotomic conjugate point) と呼ぶ.
- $\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB}$ とおき, $2s = a+b+c$ とする. 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ と内接円との接点 $\mathrm A',$ $\mathrm B',$ $\mathrm C',$ 傍接円との接点 $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ は $\mathrm{BA}' = \mathrm{CA}'' = s-b,$ $\mathrm{CB}' = \mathrm{AB}'' = s-c,$ $\mathrm{AC}' = \mathrm{BC}'' = s-a$ を満たすから, $3$ 直線 $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ の交点である「ジェルゴンヌ点」と $3$ 直線 $\mathrm{AA}'',$ $\mathrm{BB}'',$ $\mathrm{CC}''$ の交点である「ナーゲル点」(前問を参照) は互いに「等長共役点」の関係にある.
- $3$ 点 $\mathrm A(\vec a),$ $\mathrm B(\vec b),$ $\mathrm C(\vec c)$ を頂点とする $\triangle\mathrm{ABC}$ において, 各辺またはその延長上にない点 $\mathrm P(\vec p)$ の位置ベクトルが \[\vec p = \frac{\alpha\vec a+\beta\vec b+\gamma\vec c}{\alpha +\beta +\gamma}\] であるとき, 点 $\mathrm Q(\vec q)$ の「等長共役点」の位置ベクトルは \[\vec q = \frac{\alpha ^{-1}\vec a+\beta ^{-1}\vec b+\gamma ^{-1}\vec c}{\alpha ^{-1}+\beta ^{-1}+\gamma ^{-1}}\] であることが知られている.
問題《三角形に関する等角共役点》
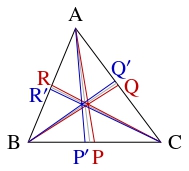
$\triangle\mathrm{ABC}$ の辺 $\mathrm{BC}$ 上に点 $\mathrm P,$ $\mathrm P',$ 辺 $\mathrm{CA}$ 上に点 $\mathrm Q,$ $\mathrm Q',$ 辺 $\mathrm{AB}$ 上に $\mathrm R,$ $\mathrm R'$ があり,
\[\angle\mathrm{BAP} = \angle\mathrm{CAP}', \quad \angle\mathrm{CBQ} = \angle\mathrm{ABQ}', \quad \angle\mathrm{ACR} = \angle\mathrm{BCR}'\]
を満たし, $3$ 本の直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点で交わるとする.
このとき, $3$ 本の直線 $\mathrm{AP}',$ $\mathrm{BQ}',$ $\mathrm{CR}'$ も $1$ 点で交わることを示せ.

解答例
$A = \angle\mathrm A,$ $B = \angle\mathrm B,$ $C = \angle\mathrm C,$ $\alpha = \angle\mathrm{BAP},$ $\beta = \angle\mathrm{CBQ},$ $\gamma = \angle\mathrm{ACR}$ とおく.
$3$ 本の直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点で交わるとき, チェヴァの定理により
\[\begin{aligned}
&1 = \frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} \\
&= \frac{\triangle\mathrm{ABP}}{\triangle\mathrm{APC}}\cdot\frac{\triangle\mathrm{BCQ}}{\triangle\mathrm{BQA}}\cdot\frac{\triangle\mathrm{CAR}}{\triangle\mathrm{CRB}} \\
&= \frac{\dfrac{1}{2}\mathrm{AB}\cdot\mathrm{AP}\sin\alpha}{\dfrac{1}{2}\mathrm{AP}\cdot\mathrm{AC}\sin (A-\alpha )}\cdot\frac{\dfrac{1}{2}\mathrm{BC}\cdot\mathrm{BQ}\sin\beta}{\dfrac{1}{2}\mathrm{BQ}\cdot\mathrm{BA}\sin (B-\beta )} \\
&\qquad \cdot\frac{\dfrac{1}{2}\mathrm{CA}\cdot\mathrm{CR}\sin\gamma}{\dfrac{1}{2}\mathrm{CR}\cdot\mathrm{CB}\sin (C-\gamma )} \\
&= \frac{\sin\alpha}{\sin (A-\alpha )}\cdot\frac{\sin\beta}{\sin (B-\beta )}\cdot\frac{\sin\gamma}{\sin (C-\gamma )} \\
\end{aligned}\]
が成り立ち,
\[\begin{aligned}
&\frac{\mathrm{BP}'}{\mathrm P'\mathrm C}\cdot\frac{\mathrm{CQ}'}{\mathrm Q'\mathrm A}\cdot\frac{\mathrm{AR}'}{\mathrm R'\mathrm B} \\
&= \frac{\triangle\mathrm{ABP}'}{\triangle\mathrm{AP}'\mathrm C}\cdot\frac{\triangle\mathrm{BCQ}'}{\triangle\mathrm{BQ}'\mathrm A}\cdot\frac{\triangle\mathrm{CAR}'}{\triangle\mathrm{CR}'\mathrm B} \\
&= \frac{\dfrac{1}{2}\mathrm{AB}\cdot\mathrm{AP}'\sin (A-\alpha )}{\dfrac{1}{2}\mathrm{AP}'\cdot\mathrm{AC}\sin\alpha}\cdot\frac{\dfrac{1}{2}\mathrm{BC}\cdot\mathrm{BQ}'\sin (B-\beta )}{\dfrac{1}{2}\mathrm{BQ}'\cdot\mathrm{BA}\sin\beta} \\
&\qquad \cdot\frac{\dfrac{1}{2}\mathrm{CA}\cdot\mathrm{CR}'\sin (C-\gamma )}{\dfrac{1}{2}\mathrm{CR}'\cdot\mathrm{CB}\sin\gamma} \\
&= \frac{\sin (A-\alpha )}{\sin\alpha}\cdot\frac{\sin (B-\beta )}{\sin\beta}\cdot\frac{\sin (C-\gamma )}{\sin\gamma} = 1
\end{aligned}\]
が成り立つから, チェヴァの定理の逆により $3$ 本の直線 $\mathrm{AP}',$ $\mathrm{BQ}',$ $\mathrm{CR}'$ も $1$ 点で交わる.
参考
- $\angle\mathrm{XOY}$ の二等分線上の点 $\mathrm M,$ 線分 $\mathrm{XY}$ 上の点 $\mathrm P,$ $\mathrm P'$ に対して $3$ つの条件
は同値である.(i) $\angle\mathrm{MOP} = \angle\mathrm{MOP}'$ (ii) $\angle\mathrm{XOP} = \angle\mathrm{YOP}'$ (iii) $\angle\mathrm{YOP} = \angle\mathrm{XOP}'$ - 本問において, $3$ 本の直線 $\mathrm{AP}',$ $\mathrm{BQ}',$ $\mathrm{CR}'$ の交点を $3$ 本の直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ の交点の「等角共役点」(isogonal conjugate point) と呼ぶ.
- $\triangle\mathrm{ABC}$ において, 重心の「等角共役点」を「類似重心」または「ルモワーヌ点」(Lemoine point) と呼ぶ.
また, 外心 $\mathrm O,$ 垂心 $\mathrm H$ は, 円周角の定理により
\[\begin{aligned}
\angle\mathrm{BAO} &= \angle\mathrm{CAH} = 90^\circ -\angle\mathrm C, \\
\angle\mathrm{CBO} &= \angle\mathrm{ABH} = 90^\circ -\angle\mathrm A, \\
\angle\mathrm{ACO} &= \angle\mathrm{BCH} = 90^\circ -\angle\mathrm B
\end{aligned}\]
を満たすから, 互いに「等角共役点」の関係にある.
なお, 内心の「等角共役点」は内心そのものである.
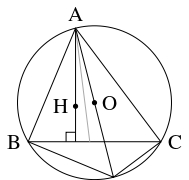
- 三角形において, 内部にある互いに共役な $2$ 点から各辺に下ろした垂線の足 $6$ 個は同一円周上にあることが知られている (「九点円」の一般化).
問題《シュタイナーの比の定理と三角形の類似重心》
- (1)
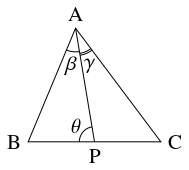
- $\triangle\mathrm{ABC}$ において, $\mathrm P$ を辺 $\mathrm{BC}$ 上の点とし, $\angle\mathrm A$ の内角の二等分線に関して $\mathrm{AP}$ と対称な直線と辺 $\mathrm{BC}$ の交点を $\mathrm P'$ とおく.
- ①
- $\mathrm{AB},$ $\mathrm{AC}$ と $\beta = \angle\mathrm{BAP},$ $\gamma = \angle\mathrm{CAP},$ $\theta = \angle\mathrm{APB}$ を用いて $\dfrac{\mathrm{BP}}{\mathrm{AB}},$ $\dfrac{\mathrm{CP}}{\mathrm{AC}}$ を表せ.
- ②
- $\mathrm{AB},$ $\mathrm{AC}$ を用いて $\dfrac{\mathrm{BP}}{\mathrm{PC}}\cdot\dfrac{\mathrm{BP}'}{\mathrm P'\mathrm C}$ を表せ.
- (2)
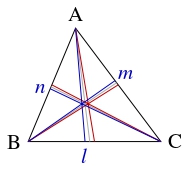
- $\triangle\mathrm{ABC}$ において, $\angle\mathrm A,$ $\angle\mathrm B,$ $\angle\mathrm C$ の内角の二等分線に関して頂点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ を通る中線と対称な直線をそれぞれ $l,$ $m,$ $n$ とする.
このとき, $l,$ $m,$ $n$ は $1$ 点で交わることを示せ.
解答例
- (1)
- ①
- $\triangle\mathrm{ABP},$ $\triangle\mathrm{ACP}$ に正弦定理を適用すると,
\[\begin{aligned}
\frac{\mathrm{BP}}{\mathrm{AB}} &= \frac{\sin\beta}{\sin\theta} \quad \cdots [1], \\
\frac{\mathrm{CP}}{\mathrm{AC}} &= \frac{\sin\gamma}{\sin (180^\circ -\theta )} = \frac{\sin\gamma}{\sin\theta} \quad \cdots [2]
\end{aligned}\]
が得られる.
- ②
- $[1]\div [2]$ から, \[\frac{\mathrm{BP}}{\mathrm{CP}} = \frac{\mathrm{AB}}{\mathrm{AC}}\cdot\frac{\sin\beta}{\sin\gamma} \quad \cdots [3]\] が成り立つ. $\angle\mathrm{BAP}' = \gamma,$ $\angle\mathrm{CAP}' = \beta$ であるから, 同様に \[\frac{\mathrm{BP'}}{\mathrm{CP'}} = \frac{\mathrm{AB}}{\mathrm{AC}}\cdot\frac{\sin\gamma}{\sin\beta} \quad \cdots [4]\] が成り立つ. ゆえに, $[3]\times [4]$ から, \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{BP}'}{\mathrm P'\mathrm C} = \frac{\mathrm{AB}^2}{\mathrm{AC}^2}\] が得られる.
- (2)
- 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の中点をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおき, $l,$ $m,$ $n$ と辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の交点をそれぞれ $\mathrm P',$ $\mathrm Q',$ $\mathrm R'$ とおく. このとき, (1) の結果により \[\begin{aligned} \frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{BP}'}{\mathrm P'\mathrm C} &= \frac{\mathrm{AB}^2}{\mathrm{AC}^2} \quad \cdots [5], \\ \frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{CQ}'}{\mathrm Q'\mathrm A} &= \frac{\mathrm{BC}^2}{\mathrm{BA}^2} \quad \cdots [6], \\ \frac{\mathrm{AR}}{\mathrm{RB}}\cdot\frac{\mathrm{AR}'}{\mathrm R'\mathrm B} &= \frac{\mathrm{CA}^2}{\mathrm{CB}^2} \quad \cdots [7] \end{aligned}\] が成り立つ. また, $\triangle\mathrm{ABC}$ の $3$ 本の中線が $1$ 点で交わることとチェヴァの定理により \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = 1\] であるから, $[5]$~$[7]$ の辺々を掛け合わせると \[\frac{\mathrm{BP}'}{\mathrm P'\mathrm C}\cdot\frac{\mathrm{CQ}'}{\mathrm Q'\mathrm A}\cdot\frac{\mathrm{AR}'}{\mathrm R'\mathrm B} = 1\] が得られる.
参考
- (1) で示した通り, $\triangle\mathrm{ABC}$ の辺 $\mathrm{BC}$ 上の点 $\mathrm P,$ $\mathrm P'$ が互いに「等角共役点」(前問を参照) の関係にあるとき, \[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{BP}'}{\mathrm P'\mathrm C} = \frac{\mathrm{AB}^2}{\mathrm{AC}^2}\] が成り立つ. これは「シュタイナーの比の定理」(Steiner's ratio theorem) として知られている.
- 三角形において, 角の頂点を通る直線 $l,$ $l'$ がその角の二等分線に関して対称であるとき, $l,$ $l'$ は互いに「等角共役線」(isogonal conjugate line) であるという. 特に, 三角形の中線の「等角共役線」を「類似中線」(symmedian) と呼ぶ (作図法についてはこちらを参照).
- $\triangle\mathrm{ABC}$ において, $3$ 本の「類似中線」の交点を「類似重心」または「ルモワーヌ点」(Lemoine point) と呼ぶ. これは重心の「等角共役点」である.
問題《三角形のキーペルト点》
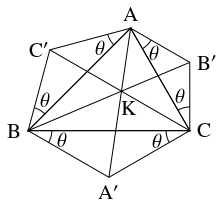
$\triangle\mathrm{ABC}$ の外側に, $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ を底辺とし, $\theta$ を底角の大きさとする, 互いに相似な二等辺三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかく.
- (1)
- $\mathrm{BC}$ と $\mathrm{AA}',$ $\mathrm{CA}$ と $\mathrm{BB}',$ $\mathrm{AB}$ と $\mathrm{CC}'$ の交点をそれぞれ $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ とおく. $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB},$ $A = \angle\mathrm{CAB},$ $B = \angle\mathrm{ABC},$ $C = \angle\mathrm{BCA}$ と $\theta$ を用いて, 線分の長さの比 $\mathrm{BP}:\mathrm{PC},$ $\mathrm{CQ}:\mathrm{QA},$ $\mathrm{AR}:\mathrm{RB}$ を表せ.
- (2)
- $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ は $1$ 点 $\mathrm K$ で交わることを示せ.

解答例
- (1)
- $\mathrm{BA}' = \mathrm{CA}'$ であるから, \[\begin{aligned} &\mathrm{BP}:\mathrm{PC} = \triangle\mathrm{AA}'\mathrm B:\triangle\mathrm{AA}'\mathrm C \\ &= \frac{1}{2}c\cdot\mathrm{BA}'\sin (B+\theta ):\frac{1}{2}b\cdot\mathrm{CA}'\sin (C+\theta ) \\ &= c\sin (B+\theta ):b\sin (C+\theta ) \end{aligned}\] が成り立つ. 同様に, \[\begin{aligned} \mathrm{CQ}:\mathrm{QA} &= a\sin (C+\theta ):c\sin (A+\theta ), \\ \mathrm{AR}:\mathrm{RB} &= b\sin (A+\theta ):a\sin (B+\theta ) \end{aligned}\] である.
- (2)
- (1) の結果により \[\begin{aligned} &\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} \\ &= \frac{c\sin (B+\theta )}{b\sin (C+\theta )}\cdot\frac{a\sin (C+\theta )}{c\sin (A+\theta )}\cdot\frac{b\sin (A+\theta )}{a\sin (B+\theta )} \\ &= 1 \end{aligned}\] であるから, チェヴァの定理の逆により直線 $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ は $1$ 点で交わる.
参考
- (2) において, $\mathrm{AA}',$ $\mathrm{BB}',$ $\mathrm{CC}'$ の交点 $\mathrm K$ は $\triangle\mathrm{ABC}$ の「キーペルト点」(Kiepert point) と呼ばれる.
- $\theta = 30^\circ$ の場合の「キーペルト点」は「(第一) ナポレオン点」(first Napoleon point) と呼ばれる.
- $\theta = 60^\circ$ の場合の「キーペルト点」は「(第一) フェルマー点」(first Fermat point) と呼ばれ, $3$ つの内角の大きさが $120^\circ$ 未満とき $3$ 頂点までの距離の和が最小の点として定まる.
- 三角形の重心, 垂心はそれぞれ $\theta = 0^\circ,$ $90^\circ$ の場合の「キーペルト点」と解釈できる.
