円周
円周の方程式
定理《円周の方程式》
点 $(a,b)$ を中心とする半径 $r$ の円周の方程式は,
\[ (x-a)^2+(y-b)^2 = r^2\]
である.
証明
点 $\mathrm C(a,b)$ を中心とする半径 $r$ の円周を $C$ とおくと, 平面上の点 $\mathrm P(x,y)$ に対して
\[\begin{aligned}
\mathrm P \in C &\iff \mathrm{CP} = r \iff \mathrm{CP}^2 = r^2 \\
&\iff (x-a)^2+(y-b)^2 = r^2
\end{aligned}\]
となるから, $C$ の方程式は $(x-a)^2+(y-b)^2 = r^2$ である.
問題《$2$ 点を直径の両端とする円周の方程式》
$2$ 点 $\mathrm P_1(x_1,y_1),$ $\mathrm P_2(x_2,y_2)$ を直径の両端とする円周 $C$ は
\[ (x-x_1)(x-x_2)+(y-y_1)(y-y_2) = 0 \quad \cdots [*]\]
で表されることを示せ.
解答例
平面上の $\mathrm P_1,$ $\mathrm P_2$ でない点 $\mathrm P(x,y)$ に対して
\[\begin{aligned}
&\mathrm P \in C \\
&\iff \mathrm{PP_1} \perp \mathrm{PP_2} \\
&\iff \frac{y-y_1}{x-x_1}\cdot\frac{y-y_2}{x-x_2} = -1 \\
&\iff (y-y_1)(y-y_2) = -(x-x_1)(x-x_2) \\
&\iff (x-x_1)(x-x_2)+(y-y_1)(y-y_2) = 0\ \cdots [*]
\end{aligned}\]
が成り立つ.
また, $(x,y) = (x_1,y_1),$ $(x_2,y_2)$ も $[*]$ を満たすから, 点 $\mathrm P_1,$ $\mathrm P_2$ も曲線 $[*]$ 上にある.
ゆえに, $C$ は $[*]$ で表される.
別解
$C$ は, 点 $\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)$ を中心とする半径 $\dfrac{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}{2}$ の円周であるから,
\[\left( x-\frac{x_1+x_2}{2}\right) ^2+\left( y-\frac{y_1+y_2}{2}\right) ^2 = \frac{(x_2-x_1)^2+(y_2-y_1)^2}{4}\]
で表される.
両辺を展開すると
\[\begin{aligned}
&x^2-(x_1+x_2)x+\frac{(x_1+x_2)^2}{4} +y^2-(y_1+y_2)y+\frac{(y_1+y_2)^2}{4} \\
&= \frac{(x_1+x_2)^2-4x_1x_2+(y_1+y_2)^2-4y_1y_2}{4}
\end{aligned}\]
となるから, $C$ は
\[ x^2-(x_1+x_2)x+x_1x_2+y^2-(y_1+y_2)y+y_1y_2 = 0\]
つまり $[*]$ で表される.
円周と直線
問題《方べきの定理》
$a,$ $b,$ $c$ を $a^2+b^2 > c$ なる実数とする.
円周 $C:x^2+y^2+2ax+2by+c = 0$ と原点 $\mathrm O$ を通る直線 $l:y = mx$ が $2$ つの共有点 $\mathrm P,$ $\mathrm Q$ をもつとき,
$\mathrm{OP}\cdot\mathrm{OQ}$ の値は $m$ の値によらず一定であることを示せ.
ただし, $C$ と $l$ が接するときは, $\mathrm P = \mathrm Q$ と考える.
解答例
点 $\mathrm P,$ $\mathrm Q$ の $x$ 座標をそれぞれ $p,$ $q$ とおく.
これらは, $C,$ $l$ の方程式から $y$ を消去して得られる $2$ 次方程式
\[ x^2+m^2x^2+2ax+2bmx+c = 0\]
つまり
\[ (1+m^2)x^2+2(a+bm)x+c = 0\]
の解であるから, 解と係数の関係により
\[ pq = \frac{c}{1+m^2}\]
が成り立つ.
また,
\[\begin{aligned}
\mathrm{OP} &= \sqrt{p^2+m^2p^2} = \sqrt{1+m^2}|p|, \\
\mathrm{OQ} &= \sqrt{q^2+m^2q^2} = \sqrt{1+m^2}|q|
\end{aligned}\]
であるから,
\[\mathrm{OP}\cdot\mathrm{OQ} = (1+m^2)|pq| = (1+m^2)\cdot\frac{|c|}{1+m^2} = |c|\]
が成り立つ.
この値は $m$ の値によらず一定である.
参考
「解析幾何学」的な方法により, 次の方べきの定理の $3$ つの場合を同時に証明できた.
ベクトルを利用した証明もある (こちらを参照).
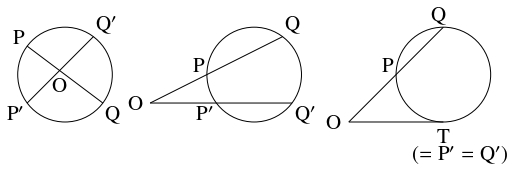
- (i)
- 円の $2$ 本の弦 $\mathrm{PQ},$ $\mathrm P'\mathrm Q'$ が円の内部の点 $\mathrm O$ で交わるとき, $\mathrm{OP}\cdot\mathrm{OQ} = \mathrm{OP}'\cdot\mathrm{OQ}'$ が成り立つ.
- (ii)
- 円の $2$ 本の弦 $\mathrm{PQ},$ $\mathrm P'\mathrm Q'$ の延長が円の外部の点 $\mathrm O$ で交わるとき, $\mathrm{OP}\cdot\mathrm{OQ} = \mathrm{OP}'\cdot\mathrm{OQ}'$ が成り立つ.
- (iii)
- 円の外部の点 $\mathrm O$ を通る直線が円と $2$ 点 $\mathrm P,$ $\mathrm Q$ で交わり, 点 $\mathrm O$ から円に引いた接線が点 $\mathrm T$ で接するとき, $\mathrm{OP}\cdot\mathrm{OQ} = \mathrm{OT}^2$ が成り立つ.

問題《ピタゴラスの $3$ つ組の公式の幾何学的証明》
座標平面において, 点 $\mathrm A(-1,0)$ を通る傾き $t$ の直線と単位円周の交点を $\mathrm P(x,y)$ $(x,\ y > 0)$ とおく.
- (1)
- $t$ を用いて $x,$ $y$ を表せ.
- (2)
- $x,$ $y$ が有理数のとき, $t$ は有理数であることを示せ.
- (3)
- $t$ を $0 < t < 1$ なる有理数とする. このとき, $x,$ $y$ は互いに素な正の整数 $m,$ $n$ $(m > n)$ を用いて \[ x = \frac{m^2-n^2}{m^2+n^2}, \quad y = \frac{2mn}{m^2+n^2} \quad \cdots [\text A]\] と表されることを示せ.
- (4)
- $a,$ $b$ の偶奇は異なる.
- (5)
- $a$ が奇数, $b$ が偶数であるとする. このとき, $a,$ $b,$ $c$ は互いに素で偶奇の異なる正の整数 $m,$ $n$ $(m > n)$ を用いて \[ a = m^2-n^2, \quad b = 2mn, \quad c = m^2+n^2 \quad \cdots [\text B]\] と表される.
解答例
- (1)
- 点 $\mathrm A(-1,0)$ を通る傾き $t$ の直線の方程式は
\[ y = t(x+1) \quad \cdots [1],\]
単位円周の方程式は
\[ x^2+y^2 = 1 \quad \cdots [2]\]
である.
点 $\mathrm P(x,y)$ はこれらの交点であるから, $[1],$ $[2]$ から $y$ を消去した \[ (1+t^2)x^2+2t^2x+(t^2-1) = 0\] を満たす. $-1$ もこの方程式の解であるから, 解と係数の関係により \[ x-1 = -\frac{2t^2}{1+t^2}\] が成り立つ. よって, \[\begin{aligned} x &= 1-\frac{2t^2}{1+t^2} = \frac{1-t^2}{1+t^2} \quad \cdots [3], \\ y &= t\left(\frac{1-t^2}{1+t^2}+1\right) = \frac{2t}{1+t^2} \quad \cdots [4] \end{aligned}\] が得られる.

- (2)
- $x,$ $y$ が有理数のとき, \[ t = \frac{y}{x+1}\] は有理数である.
- (3)
- 互いに素な正の整数 $m,$ $n$ を用いて $t = \dfrac{n}{m}$ とおくと, $[3],$ $[4]$ から \[\begin{aligned} x &= \frac{1-\dfrac{n^2}{m^2}}{1+\dfrac{n^2}{m^2}} = \frac{m^2-n^2}{m^2+n^2}, \\ y &= \frac{2\cdot\dfrac{n}{m}}{1+\dfrac{n^2}{m^2}} = \frac{2mn}{m^2+n^2} \end{aligned}\] となる. $x > 0,$ $m^2+n^2 > 0$ であるから, $m^2-n^2 > 0$ よって $m > n$ である.
- (4)
- $a,$ $b$ の偶奇が一致するとして, 矛盾を導く.
- (i)
- $a,$ $b$ が偶数であるとき. $a^2+b^2 = c^2$ は偶数になり, よって $c$ は偶数になるが, これは $a,$ $b,$ $c$ が互いに素であることに反する.
- (ii)
- $a,$ $b$ が奇数であるとき. すべての整数は $2d$ または $2d+1$ ($d$: 整数) の形に表され, \[\begin{aligned} (2d)^2 &= 4d^2, \\ (2d+1)^2 &= 4(d^2+d)+1 \end{aligned}\] を $4$ で割った余りはそれぞれ $0,$ $1$ である. よって, $a^2+b^2 = c^2$ を $4$ で割った余りは $1+1 = 2$ となるが, これは $c^2$ を $4$ で割った余りが $0$ または $1$ であることに反する.
- (5)
- $(x,y) = \left(\dfrac{a}{c},\dfrac{b}{c}\right)$ は $x^2+y^2 = 1$ の正の有理数解であるから, (3) の結果から $x,$ $y$ は互いに素な正の整数 $m,$ $n\ (m > n)$ を用いて $[\text A]$ のように表せる.
よって,
\[ a:b:c = (m^2-n^2):2mn:(m^2+n^2)\]
であり, $a,$ $b,$ $c$ は互いに素である (比 $a:b:c$ はこれ以上簡単にならない) から, ある正の整数 $k$ に対して
\[ ka = m^2-n^2, \quad kb = 2mn, \quad kc = m^2+n^2\]
となる.
\[ k(c+a) = 2m^2, \quad k(c-a) = 2n^2\]
から $k$ は $2m^2,$ $2n^2$ の公約数であるが, $m,$ $n$ は互いに素であるから, $k = 1$ または $k = 2$ である.
$m,$ $n$ がともに奇数であるとすると, $mn = k\cdot\dfrac{b}{2}$ は奇数になるから, $k = 1$ となり, $a = m^2-n^2$ となって, $a$ は偶数になるが, これは $a$ が奇数であることに反する.
よって, $m,$ $n$ の偶奇は異なる. これから $ka = m^2-n^2$ は奇数であることが言えて, $k = 1$ が言える. これで, 求める表示 $[\text B]$ が得られた.
参考
- $a^2+b^2 = c^2$ の正の整数解を「ピタゴラスの $3$ つ組」(Pythagorean triple) または「ピタゴラス数」と呼ぶ. $(a,b,c)$ が「ピタゴラスの $3$ つ組」であるとき, 各正の整数 $k$ に対して $(ka,kb,kc)$ も「ピタゴラスの $3$ つ組」になる. よって,「ピタゴラスの方程式」の一般解を求めるには, $a,$ $b,$ $c$ が互いに素であるような「ピタゴラスの $3$ つ組」$(a,b,c)$ を求めればよい. このような「ピタゴラスの $3$ つ組」は「原始的」であるという.
- 「原始的なピタゴラスの $3$ つ組」$(a,b,c)$ と, $x^2+y^2 = 1$ の正の有理数解 $(x,y)$ は, $(x,y) = \left(\dfrac{a}{c},\dfrac{b}{c}\right)$ という関係によって $1$ 対 $1$ に対応している.
本問では, 円周 $x^2+y^2 = 1$ 上の「有理点」($x$ 座標, $y$ 座標が有理数である点) を求め, この対応を使ってすべての「原始的なピタゴラスの $3$ つ組」を表す公式
($m,$ $n$: 互いに素で偶奇の異なる整数, $m > n > 0$) を導いた.
$(m^2-n^2,2mn,m^2+n^2)$ または $(2mn,m^2-n^2,m^2+n^2) \quad \cdots [*]$ - このような整数 $m,$ $n$ の組は無限に存在するから (例えば, 奇数の素数 $m$ と $n = 2$ の組は無限にある),「原始的なピタゴラスの $3$ つ組」は無限に存在する.
- 本問で示した公式の応用, 別証明については, こちらとこちらを参照されたい.
円周の接線
定理《円周の接線》
点 $(a,b)$ を中心とする半径 $r$ の円周のその上の点 $(x_0,y_0)$ における接線の方程式は,
\[ (x_0-a)(x-a)+(y_0-b)(y-b) = r^2\]
である.
証明
平行移動を考えることにより, 原点を中心とする半径 $r$ の円周 $x^2+y^2 = r^2$ について, 点 $\mathrm P_0(x_0,y_0)$ における接線 $l$ の方程式が $x_0x+y_0y = r^2$ であることを示せばよい.
- (i)
- $\mathrm P_0$ が座標軸上にないとき. 直線 $\mathrm O\mathrm P_0$ の傾きは $\dfrac{y_0}{x_0}$ であるから, $l$ の傾きは $-\dfrac{x_0}{y_0}$ である. よって, $l$ の方程式は \[\begin{aligned} y-y_0 &= -\frac{x_0}{y_0}(x-x_0) \\ x_0x+y_0y &= x_0{}^2+y_0{}^2 \\ x_0x+y_0y &= r^2 \quad \cdots [1] \end{aligned}\] である.
- (ii)
- $\mathrm P_0$ が $x$ 軸上にあるとき. $l$ の方程式は $x = r$ または $x = -r$ である. $y_0 = 0$ であるから, これは $[1]$ で表される.
- (iii)
- $\mathrm P_0$ が $y$ 軸上にあるとき. $l$ の方程式は $y = r$ または $y = -r$ である. $x_0 = 0$ であるから, これは $[1]$ で表される.
別証明
平行移動を考えることにより, $a = b = 0$ の場合を示せばよい.
円周 $x^2+y^2 = r^2$ の点 $\mathrm P_0(x_0,y_0)$ における接線は, 点 $(x_0,y_0)$ を通り, 法線ベクトルが $(x_0,y_0)$ の直線である.
よって, その方程式は
\[\begin{aligned}
x_0(x-x_0)+y_0(y-y_0) &= 0 \\
x_0x+y_0y &= x_0{}^2+y_0{}^2 \\
x_0x+y_0y &= r^2
\end{aligned}\]
である.
問題《円周の接線》
原点を中心とする半径 $r$ の円周に接する傾き $m$ の直線の方程式を求めよ.
解答例
求める直線の方程式を $y = mx+n$ とおく.
原点と直線 $mx-y+n = 0$ の距離は $r$ であるから,
\[\frac{|m\cdot 0-0+n|}{\sqrt{m^2+(-1)^2}} = r\]
が成り立つ.
よって, $|n| = r\sqrt{1+m^2}$ つまり $n = \pm r\sqrt{1+m^2}$ であるから, 求める直線の方程式は
\[ y = mx\pm r\sqrt{1+m^2}\]
である.
問題《円周の極線》
原点を中心とする半径 $r$ の円の外部の相異なる点 $\mathrm P(a,b),$ $\mathrm P'(a',b'),$ $\mathrm P''(a'',b'')$ からその周に引いた $2$ 本の接線の接点をそれぞれ $\mathrm T_1$ および $\mathrm T_2,$ $\mathrm T'_1$ および $\mathrm T'_2,$ $\mathrm T''_1$ および $\mathrm T''_2$ とおく.
次のことを示せ.
- (1)
- 直線 $\mathrm T_1\mathrm T_2$ の方程式は \[ ax+by = r^2\] である.
- (2)
- 直線 $\mathrm T_1\mathrm T_2$ が点 $\mathrm P'$ を通るとする. このとき, 直線 $\mathrm T'_1\mathrm T'_2$ は点 $\mathrm P$ を通る.
- (3)
- 直線 $\mathrm T_1\mathrm T_2,$ $\mathrm T'_1\mathrm T'_2$ が点 $\mathrm P''$ を通るとする. このとき, 直線 $\mathrm T''_1\mathrm T''_2$ は直線 $\mathrm P\mathrm P'$ と一致する.
解答例
- (1)
- $\mathrm T_1(x_1,y_1),$ $\mathrm T_2(x_2,y_2)$ とおく.
点 $\mathrm T_1,$ $\mathrm T_2$ における接線の方程式は,
\[ x_1x+y_1y = r^2, \quad x_2x+y_2y = r^2\]
である.
これらの直線は点 $\mathrm P(a,b)$ を通るから,
\[ ax_1+by_1 = r^2, \quad ax_2+by_2 = r^2\]
が成り立つ.
これは, 直線 $ax+by = r^2$ が点 $\mathrm T_1,$ $\mathrm T_2$ を通ることを意味している.
ゆえに, 直線 $\mathrm T_1\mathrm T_2$ の方程式は,
\[ ax+by = r^2\]
である.
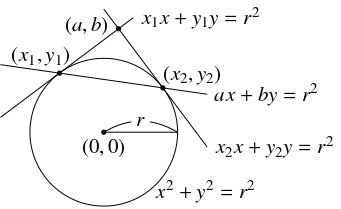
- (2)
- (1) により, 直線 $\mathrm T'_1\mathrm T'_2$ の方程式は $a'x+b'y = r^2$ である. 直線 $\mathrm T_1\mathrm T_2$ つまり $ax+by = r^2$ は点 $\mathrm P'(a',b')$ を通るから, \[ a'a+b'b = r^2\] が成り立つ. これは, 直線 $\mathrm T'_1\mathrm T'_2$ が点 $\mathrm P(a,b)$ を通ることを意味している.
- (3)
- (1) により, 直線 $\mathrm T_1\mathrm T_2,$ $\mathrm T'_1\mathrm T'_2,$ $\mathrm T''_1\mathrm T''_2$ の方程式はそれぞれ \[ ax+by = r^2, \quad a'x+b'y = r^2, \quad a''x+b''y = r^2\] である. 直線 $\mathrm T_1\mathrm T_2,$ $\mathrm T'_1\mathrm T'_2$ が点 $\mathrm P''(a'',b'')$ を通ることから, \[ a''a+b''b = r^2, \quad a''a'+b''b' = r^2\] が成り立つ. これは, 直線 $\mathrm T''_1\mathrm T''_2$ が点 $\mathrm P(a,b),$ $\mathrm P'(a',b')$ を通ること, つまり直線 $\mathrm T''_1\mathrm T''_2$ が直線 $\mathrm{PP}'$ と一致することを意味している.
参考
- 直線 $\mathrm T_1\mathrm T_2$ を点 $\mathrm P$ に関する円周の「極線」(polar line, polar) と呼び, 点 $\mathrm P$ をその「極」(pole) と呼ぶ.
- 点 $\mathrm P$ に関する円周 $C$ の「極線」を $\mathrm P^*$ で表すとき, (2) は
\[\mathrm Q \in \mathrm P^* \iff \mathrm P \in \mathrm Q^*\]
が成り立つということである.
これは, しばしば「共役定理」と呼ばれる.
このことを使うと, 例えば, 点 $\mathrm P_1,$ $\mathrm P_2,$ $\mathrm P_3$ に対して,
$\mathrm Q \in \mathrm P_k{}^*$ $\iff$ $\mathrm P_k \in \mathrm Q^*$ $(k = 1,\ 2,\ 3)$ から,
$\mathrm P_1{}^*,$ $\mathrm P_2{}^*,$ $\mathrm P_3{}^*$ は $1$ 点で交わるの成り立つことがわかる.
$\iff$ $\mathrm P_1,$ $\mathrm P_2,$ $\mathrm P_3$ は $1$ 直線上にある - (2), (3)の結果とこれらの事実は, $2$ 次曲線に一般化される (こちらを参照).
問題《$2$ 円の根軸》
$p_1,$ $q_1,$ $p_2,$ $q_2$ を $(p_1,q_1) \neq (p_2,q_2)$ なる実数, $r_1,$ $r_2$ を正の数として, $x,$ $y$ の多項式
\[\begin{aligned}
f_1(x,y) &= (x-p_1)^2+(y-q_1)^2-r_1{}^2, \\
f_2(x,y) &= (x-p_2)^2+(y-q_2)^2-r_2{}^2
\end{aligned}\]
を考える.
円周 $C_1:f_1(x,y) = 0,$ $C_2:f_2(x,y) = 0$ と直線 $l:f_1(x,y)-f_2(x,y) = 0$ について, 次のことを示せ.
- (A)
- $l$ は $C_1,$ $C_2$ に向かって長さの等しい接線が引ける点の軌跡である.
- (B)
- $C_1,$ $C_2$ が相異なる $2$ 点 $\mathrm A,$ $\mathrm B$ で交わるとき, $l$ は直線 $\mathrm{AB}$ と一致する.
- (C)
- $C_1,$ $C_2$ が点 $\mathrm T$ で接するとき, $l$ は点 $\mathrm T$ における $C_1,$ $C_2$ の共通の接線である.
解答例
$\mathrm O_1(p_1,q_1),$ $\mathrm O_2(p_2,q_2)$ とおく.
- (A)
- 点 $\mathrm P(x,y)$ から $C_1,$ $C_2$ に下ろした接線の接点を $\mathrm T_1,$ $\mathrm T_2$ とおくと,
\[\begin{aligned}
\mathrm P \in l &\iff f_1(x,y)-f_2(x,y) = 0 \\
&\iff f_1(x,y) = f_2(x,y) \\
&\iff (x-p_1)^2+(y-q_1)^2-r_1{}^2 \\
&\qquad\quad = (x-p_2)^2+(y-q_2)^2-r_2{}^2 \\
&\iff \mathrm O_1\mathrm P^2-r_1{}^2 = \mathrm O_2\mathrm P^2-r_2{}^2 \\
&\iff \mathrm{PT}_1{}^2 = \mathrm{PT}_2{}^2 \\
&\iff \mathrm{PT}_1{} = \mathrm{PT}_2
\end{aligned}\]
となるから, $l$ は $C_1,$ $C_2$ に向かって長さの等しい接線が引ける点の軌跡である.
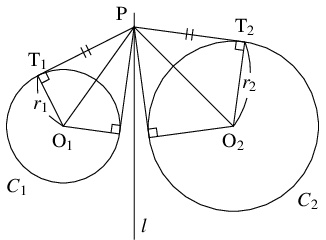
- (B)
- $C_1,$ $C_2$ が相異なる $2$ 点 $\mathrm A,$ $\mathrm B$ で交わるとする.
このとき, 連立方程式 $f_1(x,y) = 0,$ $f_2(x,y) = 0$ はこの $2$ 点に対応する $2$ つの実数解をもつ.
それらの解は $f_1(x,y)-f_2(x,y) = 0$ を満たすから, $l$ は $\mathrm A,$ $\mathrm B$ を通る.
ゆえに, $l$ は直線 $\mathrm{AB}$ と一致する.
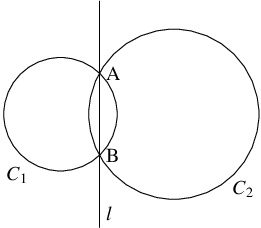
- (C)
- $C_1,$ $C_2$ が点 $\mathrm T$ で接するとする. 直線 $l$ と線分 $\mathrm O_1\mathrm O_2$ は点 $\mathrm T$ を通るから, \[ l \perp \mathrm O_1\mathrm O_2\] を示せばよい. これは, $l,$ $\mathrm O_1\mathrm O_2$ の方程式がそれぞれ \[\begin{aligned} &2(p_2-p_1)x+2(q_2-q_1)y \\ &\qquad +p_1{}^2-p_2{}^2+q_1{}^2-q_2{}^2-r_1{}^2+r_2{}^2 = 0, \\ &(q_2-q_1)x-(p_2-p_1)y-p_1q_2+p_2q_1 = 0 \end{aligned}\] であり, \[ 2(p_2-p_1)\cdot (q_2-q_1)+2(q_2-q_1)\cdot\{ -(p_2-p_1)\} = 0\] であることから従う.
参考
直線 $l$ を $2$ 円 $f_1(x,y) \leqq 0,$ $f_2(x,y) \leqq 0$ の「根軸」(radical axis) と呼ぶ.
問題《ポンスレの閉形定理にまつわる問題》
原点を中心とする半径 $1$ の円周 $C$ と放物線 $D:y = x^2-2$ について, 次の問いに答えよ.
- (A)
- $D$ の頂点 $\mathrm R(0,-2)$ から $C$ に引いた接線と $D$ の交点で $\mathrm R$ と異なるものを $\mathrm P,$ $\mathrm Q$ とおく. このとき, 直線 $\mathrm{PQ}$ も $C$ に接することを示せ.
- (B)
- $D$ 上の相異なる $3$ 点 $\mathrm P(p,p^2-2),$ $\mathrm Q(q,q^2-2),$ $\mathrm R(r,r^2-2)$ に対して, 直線 $\mathrm{PR},$ $\mathrm{QR}$ が原点を中心とする半径 $1$ の円周 $C$ に接するならば, 直線 $\mathrm{PQ}$ も円周 $C$ に接することを示せ.
(参考: $1988$ 名古屋大)
解答例
- (A)
- 点 $\mathrm R$ から $C$ に引いた接線の接点の座標を $(x_0,y_0)$ とおく.
この接線は,
\[ x_0x+y_0y = 1\]
という方程式で表され, 点 $\mathrm R(0,-2)$ を通るから,
$-2y_0 = 1$ つまり $y_0 = -\dfrac{1}{2}$である. 一方, 点 $(x_0,y_0)$ は $C$ 上にあり, $x_0{}^2+y_0{}^2 = 1$ を満たすから, \[ x_0 = \pm\frac{\sqrt 3}{2}\] である. よって, 接線 $\mathrm{PR},$ $\mathrm{QR}$ の方程式は,$\pm\dfrac{\sqrt 3}{2}x-\dfrac{1}{2}y = 1$ つまり $y = \pm\sqrt 3x-2$である. これらの接線と $D$ の交点の $x$ 座標は$x^2-2 = \pm\sqrt 3x-2$ つまり $x(x\mp \sqrt 3) = 0$の解 $x = \pm\sqrt 3$ であるから, 交点の $y$ 座標は \[ y = (\pm\sqrt 3)^2-2 = 1\] である. よって, 接線 $\mathrm{PQ}$ は, 直線 $y = 1$ であるから, $C$ に接する.
- (B)
- 直線 $\mathrm{PR}$ の方程式は
\[ y-p^2+2 = \frac{(r^2-2)-(p^2-2)}{r-p}(x-p)\]
つまり
\[ (p+r)x-y-pr-2 = 0\]
であるから, 直線 $\mathrm{PR}$ が $C$ に接する条件は
\[\frac{|-pr-2|}{\sqrt{(p+r)^2+1}} = 1\]
つまり
\[ (pr+2)^2 = (p+r)^2+1 \quad \cdots [1]\]
である.
同様に, 直線 $\mathrm{QR}$ が $C$ に接する条件は \[ (qr+2)^2 = (q+r)^2+1 \quad \cdots [2]\] である. $[1],$ $[2]$ が成り立つとき, $p,q$ は $x$ の $2$ 次方程式 \[ (rx+2)^2 = (x+r)^2+1\] つまり \[ (r^2-1)x^2+2rx+3-r^2 = 0\] の解であるから, 解と係数の関係により \[ p+q = -\frac{2r}{r^2-1}, \quad pq = \frac{3-r^2}{r^2-1}\] が成り立つ. このとき, \[\begin{aligned} (p+q)^2+1 &= \frac{4r^2}{(r^2-1)^2}+1 = \frac{4r^2+(r^2-1)^2}{(r^2-1)^2} \\ &= \frac{r^4+2r^2+1}{(r^2-1)^2} = \frac{(r^2+1)^2}{(r^2-1)^2} \\ &= \left(\frac{r^2+1}{r^2-1}\right) ^2 = \left(\frac{3-r^2}{r^2-1}+2\right) ^2 \\ &= (pq+2)^2 \end{aligned}\] となるから, 上記の議論の逆をたどることにより, 直線 $\mathrm{PQ}$ は $C$ に接することがわかる.
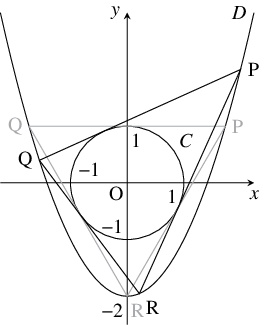
参考
本問は, 次の「ポンスレの閉形定理」(Poncelet's closure theorem) を背景としている:
$2$ 次曲線 $C,$ $D$ に対して, $C$ に外接し, $D$ に内接する $n$ 角形が $1$ つでも存在するならば,
$D$ 上の任意の点 $\mathrm P_1$ を $1$ つの頂点とし, $C$ に外接し, $D$ に内接する $n$ 角形が存在する.
つまり, 点 $\mathrm P_k$ から $C$ に引いた接線と $D$ の交点 ($\neq \mathrm P_k$) を $\mathrm P_{k+1}$ とおくことで点 $\mathrm P_2$ $\cdots,$ $\mathrm P_n,$ $\mathrm P_{n+1}$ を順次定めると,
$\mathrm P_{n+1} = \mathrm P_1$ となり, $C$ に外接し, $D$ に内接する $n$ 角形 $\mathrm P_1\mathrm P_2\cdots \mathrm P_n$ が得られる.
$C$ が円周, $D$ が放物線で, $n = 3$ である場合に限っても, 一般論を述べるには複雑な計算を要するため, 本問ではその一例を示した.
$C$ が円周, $D$ が放物線で, $n = 3$ である場合に限っても, 一般論を述べるには複雑な計算を要するため, 本問ではその一例を示した.
