立方体倍積問題
立方体倍積問題
定理《立方体倍積問題》
平面上で, 長さ $1$ の線分をもとに長さ $\sqrt[3]{2}$ の線分を定規とコンパスのみで作図することは不可能である.
高校数学の問題
複素数と方程式
問題《目盛付き定規が使える場合の立方体倍積問題》
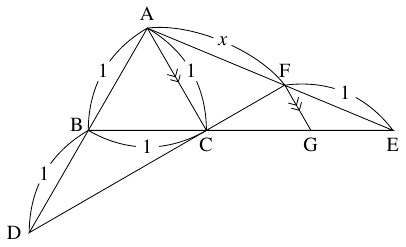
$1$ 辺の長さが $1$ の正三角形 $\mathrm{ABC}$ において, 辺 $\mathrm{AB}$ の $\mathrm B$ を越える延長上に $\mathrm{BD} = 1$ なる点 $\mathrm D$ をとる.
また, 辺 $\mathrm{BC}$ の $\mathrm C$ を越える延長上の点 $\mathrm E$ を, $\mathrm{AE}$ と $\mathrm{CD}$ の交点 $\mathrm F$ について $\mathrm{EF} = 1$ となるようにとり, $x = \mathrm{AF}$ とおく.
さらに, 点 $\mathrm F$ を通って $\mathrm{AC}$ に平行な直線と $\mathrm{BE}$ の交点を $\mathrm G$ とおく.

- (1)
- $x$ を用いて線分 $\mathrm{FG},$ $\mathrm{CF}$ の長さを表せ.
- (2)
- $x^4+2x^3-2x-4 = 0$ を示せ.
- (3)
- $x$ の値を求めよ.
解答例
こちらを参照.