階差数列
階差数列
定義《階差数列》
数列 $\{ a_n\}$ に対して, $a_{n+1}-a_n$ を一般項とする数列を $\{ a_n\}$ の階差数列(difference sequence) と呼ぶ.
定理《階差数列と一般項》
数列 $\{ a_n\}$ の階差数列が $\{ d_n\}$ であるならば,
$n \geqq 2$ のとき
\[ a_n = a_1+\sum_{k = 1}^{n-1}d_k\]
が成り立つ.
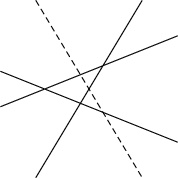
問題《シュタイナーの平面・空間の分割問題》
- (1)
- どの $2$ 本も平行でなく, どの $3$ 本も $1$ 点で交わらないように, 平面上に $n$ 本の直線をかく.
このとき, 平面が分割されてできる領域の個数 $a_n$ を求めよ.
(参考: $2019$ 横浜市立大)
- (2)
- どの $2$ 枚も平行でなく, どの $3$ 枚も直線を共有せず, どの $4$ 枚も $1$ 点で交わらないように, 空間内に $n$ 枚の平面をかく.
このとき, 空間が分割されてできる領域の個数 $b_n$ を求めよ.
(参考: $2011$ 立命館大, $2019$ 東京工業大)
解答例
- (1)
- $n$ 本の直線をかいた状態から新たに $1$ 本の直線をかいていくと,
既存の直線と交わる度に領域が $1$ 個ずつ増え, 全部で $n+1$ 個の平面領域が増えるので,
\[ a_{n+1}-a_n = n+1\]
が成り立つ.
また, $a_1 = 2$ であるから, $n \geqq 2$ のとき \[\begin{aligned} a_n &= a_1+\sum_{k = 1}^{n-1}(a_{k+1}-a_k) \\ &= 2+\sum_{k = 1}^{n-1}(k+1) \\ &= 2+\frac{(n-1)n}{2}+(n-1) \\ &= \frac{1}{2}(n^2+n+2) \end{aligned}\] が成り立つ. これは $n = 1$ のときも成り立つ.
- (2)
- $n$ 枚の平面をかいた状態から新たに $1$ 枚の平面をかいていくと, 新たな平面が既存の平面との交線 $n$ 本により分割されてできる平面領域の個数 $a_n$ だけ空間領域が増えるので, \[ b_{n+1}-b_n = a_n = \frac{1}{2}(n^2+n+2)\] が成り立つ. また, $b_1 = 2$ であるから, $n \geqq 2$ のとき \[\begin{aligned} b_n &= b_1+\sum_{k = 1}^{n-1}(b_{k+1}-b_k) \\ &= 2+\sum_{k = 1}^{n-1}\frac{1}{2}(k^2+k+2) \\ &= 2+\frac{1}{2}\left(\sum_{k = 1}^{n-1}k^2+\sum_{k = 1}^{n-1}k+\sum_{k = 1}^{n-1}2\right) \\ &= 2+\frac{1}{2}\left\{\frac{1}{6}(n-1)n(2n-1)+\frac{1}{2}(n-1)n+2(n-1)\right\} \end{aligned}\] であり, 展開して整理すると, \[\begin{aligned} b_n &= \frac{1}{6}(n+1)(n^2-n+6) \end{aligned}\] が得られる. これは $n = 1$ のときも成り立つ.
参考
- (1), (2) は「シュタイナーの分割問題」として知られている.
- 平面, 空間を円, 球に置き換えても, $n$ 本の直線, $n$ 枚の平面により分割されてできる領域の個数の最大値 $a_n,$ $b_n$ は上記の公式で与えられる. しばしば, $\{ a_n\}$ は「怠け仕出し屋の数列」(lazy caterer's sequence), $\{ b_n\}$ の項は「ケーキ数」(cake number) と呼ばれる.
- どの $2$ 本も平行でなく, どの $3$ 本も $1$ 点で交わらないような $n$ 本の直線として, 例えば, 放物線 $y = x^2$ の点 $(k,k^2)$ における接線 \[ y = 2k(x-k)+k^2\] ($k$: 整数, $1 \leqq k \leqq n$) が挙げられる. 実際, これらの直線の傾きはすべて異なるから, どの $2$ 本も平行でない. また, $1$ 点から放物線に引ける接線の本数は $2$ 本以下であるから, どの $3$ 本も $1$ 点で交わることはない.
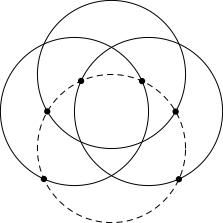
問題《円周による平面の分割》
どの $2$ 個も $2$ 点で交わり, どの $3$ 個も $1$ 点で交わらないように, 平面上に $n$ 個の円周をかく.
このとき, 平面が分割されてできる領域の個数 $a_n$ を求めよ.
解答例
$n$ 個の円周をかいた状態から新たに $1$ 個の円周をかいていくと,
既存の各円周と $2$ 点で交わり, その各交点で領域が $1$ 個ずつ増えて, 全部で $2n$ 個の領域が増えるので,
\[ a_{n+1}-a_n = 2n\]
が成り立つ.
 また, $a_1 = 2$ であるから, $n \geqq 2$ のとき
\[\begin{aligned}
a_n &= a_1+\sum_{k = 1}^{n-1}(a_{k+1}-a_k) = 2+\sum_{k = 1}^{n-1}2k \\
&= 2+2\cdot\frac{(n-1)n}{2} = n^2-n+2
\end{aligned}\]
が成り立つ.
これは $n = 1$ のときも成り立つ.
また, $a_1 = 2$ であるから, $n \geqq 2$ のとき
\[\begin{aligned}
a_n &= a_1+\sum_{k = 1}^{n-1}(a_{k+1}-a_k) = 2+\sum_{k = 1}^{n-1}2k \\
&= 2+2\cdot\frac{(n-1)n}{2} = n^2-n+2
\end{aligned}\]
が成り立つ.
これは $n = 1$ のときも成り立つ.

参考
- $1$ つの平面上に $1$ 個, $2$ 個, $3$ 個の円周をかくとき平面が分割されてできる領域の個数の最大値はそれぞれ $2 = 2^1,$ $4 = 2^2,$ $8 = 2^3$ であるから, 円を用いたヴェン図で $3$ 個以下の集合の関係が表せる (共通部分は面積が正である円の重なりとして表せる).
しかし, $n \geqq 4$ のとき, $n$ 個の円周により平面が分割されてできる領域の個数の最大値は $n^2-n+2$ で $2^n$ より小さいから, 円を用いたヴェン図で $n$ 個の集合の関係が表せるとは限らない.
不等式
\[ n^2-n+2 < 2^n \quad (n \geqq 4)\]
は, 次のように示せる:
\[ b_n = \frac{n^2-n+2}{2^n}\]
とおく.
$b_4 < 1$ であるから, $b_{n+1} < b_n$ であることを示せば,
\[\cdots < b_{n+1} < b_n < \cdots < b_4 < 1\]
となり, $b_n < 1$ つまり $n^2-n+2 < 2^n$ であることが示せる.
そこで, $b_n,$ $b_{n+1}$ の比をとると,
\[\begin{aligned}
\frac{b_{n+1}}{b_n} &= \frac{(n+1)^2-(n+1)+2}{2^{n+1}}\div\frac{n^2-n+2}{2^n} \\
&= \frac{n^2+n+2}{2(n^2-n+2)}
\end{aligned}\]
となる.
$n \geqq 4$ のとき,
\[\begin{aligned}
2(n^2-n+2)-(n^2+n+2) &= n^2-3n+2 \\
&= (n-1)(n-2) > 0
\end{aligned}\]
であるから, $0 < n^2+n+2 < 2(n^2-n+2)$ であり,
が成り立つ. したがって, $n \geqq 4$ のとき $n^2-n+2 < 2^n$ が成り立つ.$\dfrac{b_{n+1}}{b_n} < 1$ つまり $b_{n+1} < b_n$ - $n$ 個の楕円の周により平面が分割されてできる領域の個数が最大になるのは, どの $2$ 個も $4$ 点で交わり, どの $3$ 個も $1$ 点で交わらないときである. その最大値 $e_n$ は, \[ e_1 = 2, \quad e_{n+1}-e_n = 4n\] から \[\begin{aligned} e_n &= e_1+\sum_{k = 1}^{n-1}(e_{k+1}-e_k) = 2+\sum_{k = 1}^{n-1}4k \\ &= 2+4\cdot\frac{(n-1)n}{2} = 2(n^2-n+1) \end{aligned}\] である ($n = 1$ のときも成り立つ). $e_n$ の $n \leqq 5$ における値は \[ 2,\ 6,\ 14,\ 26,\ 42\] で $2^n$ 以上であるから, 楕円を用いたヴェン図で $5$ 個以下の集合の関係が表せる.
- どの $3$ 個も $1$ 点で交わらないように, 球面上に $n$ 個の「大円」(球面と球の中心を通る平面との交線) をかくとき, 平面が分割されてできる領域の個数も, $n^2-n+2$ である (証明は同様).
- $n$ 個の球面により空間が分割されてできる領域の個数の最大値は, $\dfrac{1}{3}n(n^2-3n+8)$ であり, $n \leqq 4$ のとき $2^n$ に等しいから, 球を用いた “空間におけるヴェン図” で $4$ 個以下の集合の関係が表せる.
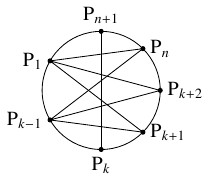
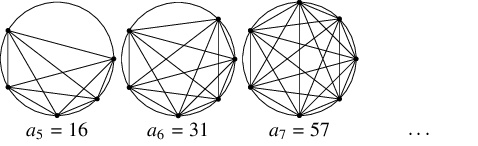
問題《モーザーの円の分割問題》
円周上に相異なる $n$ 個の点 $\mathrm P_1,$ $\cdots,$ $\mathrm P_n$ があり, 次の条件を満たすとする.
- 与えられた点は番号順に反時計回りに並ぶ.
- 与えられた点どうしをすべて弦で結んだとき, どの $3$ 本の弦も円の内部において $1$ 点で交わらない.
- (1)
- 上記の状態から, 新たな点 $\mathrm P_{n+1}$ をとり, 上記の条件を満たすようにする (与えられた点と既存の弦の交点とを通る弦は有限個しかなく, 弧 $\mathrm P_n\mathrm P_1$ 上には無限に多くの点があるから, これは可能である). $1 \leqq k \leqq n$ なる各整数 $k$ に対して, 弦 $\mathrm P_k\mathrm P_{n+1}$ を引く際に, 円が分割されてできる領域は $(k-1)(n-k)+1$ 個増えることを説明せよ.
- (2)
- $n$ を用いて $a_{n+1}-a_n$ を表せ.
- (3)
- $n$ を用いて $a_n$ を表せ.
解答例
- (1)
- 点 $\mathrm P_k$ から点 $\mathrm P_{n+1}$ に向かって弦 $\mathrm P_k\mathrm P_{n+1}$ を引いていくと,
既存の弦と交わる度に領域が $1$ 個ずつ増えて,
点 $\mathrm P_{n+1}$ に達したときに領域がさらに $1$ 個増える.
弦 $\mathrm P_k\mathrm P_{n+1}$ と交わる弦はその両側の点を結んだ $(k-1)(n-k)$ 本の弦 $\mathrm P_i\mathrm P_j$ $(1 \leqq i \leqq k-1,$ $k+1 \leqq j \leqq n)$ に限るから,
領域は全部で $(k-1)(n-k)+1$ 個増える.
- (2)
- 円周上に点 $\mathrm P_1,$ $\cdots,$ $\mathrm P_n$ しかとっていない状態から点 $\mathrm P_{n+1}$ をとって $n$ 本の弦 $\mathrm P_k\mathrm P_{n+1}$ $(1 \leqq k \leqq n)$ を引くときに増える領域の個数を考えると, (1) の結果から, \[\begin{aligned} &a_{n+1}-a_n \\ &= \sum_{k = 1}^n\{ (k-1)(n-k)+1\} \\ &= \sum_{k = 1}^n\{ -k^2+(n+1)k+(1-n)\} \\ &= -\frac{1}{6}n(n+1)(2n+1)+\frac{1}{2}n(n+1)^2+(1-n)n \\ &= \frac{1}{6}n\{ -(n+1)(2n+1)+3(n+1)^2+6(1-n)\} \\ &= \frac{1}{6}n(n^2-3n+8) \end{aligned}\] が得られる.
- (3)
- $n \geqq 2$ のとき, (2) の結果から, \[\begin{aligned} a_n &= a_1+\sum_{k = 1}^{n-1}\frac{1}{6}k(k^2-3k+8) \\ &= 1+\frac{1}{6}\sum_{k = 1}^{n-1}(k^3-3k^2+8k) \\ &= 1+\frac{1}{6}\left\{\frac{1}{4}(n-1)^2n^2\right. \\ &\qquad \left.-3\cdot\frac{1}{6}(n-1)n(2n-1)+8\cdot\frac{1}{2}(n-1)n\right\} \\ &= 1+\frac{1}{24}(n-1)n\{ (n-1)n-2(2n-1)+16\} \\ &= 1+\frac{1}{24}(n-1)n(n^2-5n+18) \\ &= \frac{1}{24}(n^4-6n^3+23n^2-18n+24) \end{aligned}\] が得られる. これは $n = 1$ のときも成り立つ. ゆえに, すべての正の整数 $n$ に対して $a_n = \dfrac{1}{24}(n^4-6n^3+23n^2-18n+24)$ が成り立つ.
参考
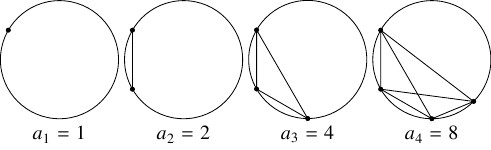
- 本問は,「モーザーの円の分割問題」(Moser's circle problem) として知られている.
- 上記の数列 $\{ a_n\}$ はしばしば「モーザー数列」と呼ばれる.
- \[ a_1 = 1, \quad a_2 = 2, \quad a_3 = 4, \quad a_4 = 8, \quad a_5 = 16\]
から $a_n = 2^{n-1}$ と推測してしまいそうだが, $a_6 = 31$ であり, $\{ a_n\}$ は等比数列ではない.
この事実は, すべてが証明されるまでは予想は覆される恐れがあるということをよく暗示している.
- 凸 $n$ 角形において, どの $3$ 本の対角線も $1$ 点で交わらないとき, $n$ 角形が対角線により分割されてできる領域の個数は,「モーザの円の分割問題」の解から点の個数を引いた数 \[\begin{aligned} &\frac{1}{24}(n^4-6n^3+23n^2-18n+24)-n \\ &= \frac{1}{24}(n^4-6n^3+23n^2-42n+24) \end{aligned}\] である.
- 正の整数 $m$ に対して, 正の整数全体を定義域とする関数 $\delta _m(n)$ を \[\delta _m(n) = \begin{cases} 1 & (n \equiv 0 \pmod m), \\ 0 & (n \not\equiv 0 \pmod m) \end{cases}\] で定める. このとき, 正 $n$ 角形が対角線により分割されてできる領域の個数は \[\begin{aligned} &\frac{n^4−6n^3+23n^2−42n+24}{24}+\frac{−5n^3+42n^2−40n−48}{48}\cdot\delta _2(n) \\ &−\frac{3n}{4}\cdot\delta _4(n)+\frac{−53n^2+310n}{12}\cdot\delta_6(n)+\frac{49n}{2}\cdot\delta _{12}(n) \\ &+32n\cdot\delta _{18}(n)+19n\cdot\delta _{24}(n)−36n\cdot\delta _{30}(n) \\ &−50n\cdot\delta _{42}(n)−190n\cdot\delta _{60}(n)−78n\cdot\delta _{84}(n) \\ &−48n\cdot\delta _{90}(n)−78n\cdot\delta _{120}(n)−48n\cdot\delta _{210}(n) \end{aligned}\] であることが知られている (B. Poonen and M. Rubinstein, "The number of intersection points made by the diagonals of a regular polygon," SIAM J. Disc. Math., 11 (1998), no. 1, 135–156).
問題《角錐の最短往復数に関する数列》
$n$ 角錐のある頂点から出発して, 辺伝いにすべての頂点を巡り, 元の頂点に戻る経路において, 通過する辺ののべ本数の最小値を $x_n$ とおく.
さらに, $a_n = x_{n-2},$ $b_n = a_{n+1}-a_n,$ $c_n = b_{n+1}-b_n$ とおく.
$a_1 = 8,$ $b_1 = 2,$ $c_n = (-1)^n$ であることが知られている.
- (1)
- 数列 $\{ b_n\}$ の一般項を求めよ.
- (2)
- 数列 $\{ a_n\},$ $\{ x_n\}$ の一般項を求めよ.
(参考: 濱田和哉,『$n$ 角柱・$n$ 角錐・正多面体の最短往復数について』,
数研通信 $86$ 号, $2016$)
数研通信 $86$ 号, $2016$)
解答例
- (1)
- $\{ b_n\}$ の一般項は, \[\begin{aligned} b_n &= b_1+\sum_{k = 1}^{n-1}c_k = 2+\sum_{k = 1}^{n-1}(-1)^k \\ &= 2+\frac{1-(-1)^{n-1}}{1-(-1)} = 2+\frac{1+(-1)^n}{2} \\ &= \frac{5}{2}+\frac{(-1)^n}{2} \end{aligned}\] である.
- (2)
- $\{ a_n\}$ の一般項は \[\begin{aligned} a_n &= a_1+\sum_{k = 1}^{n-1}b_k = 8+\sum_{k = 1}^{n-1}\left\{\frac{5}{2}+\frac{(-1)^k}{2}\right\} \\ &= 8+\frac{5}{2}(n-1)+\frac{-1}{2}\cdot\frac{1-(-1)^{n-1}}{1-(-1)} \\ &= 8+\frac{5}{2}(n-1)-\frac{1+(-1)^n}{4} \\ &= \frac{21}{4}+\frac{5}{2}n-\frac{(-1)^n}{4} \end{aligned}\] であるから, $\{ x_n\}$ の一般項は \[\begin{aligned} x_n &= a_{n-2} = \frac{21}{4}+\frac{5}{2}(n-2)-\frac{(-1)^{n-2}}{4} \\ &= \frac{1}{4}+\frac{5}{2}n-\frac{(-1)^n}{4} \end{aligned}\] である.
参考
多面体のある頂点から出発して, 辺伝いにすべての頂点を巡り, 元の頂点に戻る経路において, 通過する辺ののべ本数の最小値は,「最短往復数」と呼ばれる (濱田氏による).
いろいろな数列の和
問題《等差数列と等比数列の積の和》
$n$ を正の整数とする.
$S = \displaystyle\sum_{k = 1}^nk2^{k-1}$ の値を, 次の方法で求めよ.
- (A)
- $S,$ $2S$ の差をとる.
- (B)
- $f(x+1)-f(x) = x2^{x-1}$ を満たすような関数
$f(x) = (ax+b)2^{x-1}$ ($a,$ $b$: 実数) を利用する.
解答例
- (A)
- \[\begin{aligned} S &= 1\cdot 1+2\cdot 2+\cdots +n\cdot 2^{n-1} \\ 2S &= \qquad\quad 1\cdot 2+\cdots +(n-1)\cdot 2^{n-1}+n\cdot 2^n \end{aligned}\] の辺々を引くと, \[\begin{aligned} -S &= 1+2+\cdots +2^{n-1}-n2^n \\ &= \frac{1\cdot (2^n-1)}{2-1}-n2^n \\ &= -(n-1)2^n-1 \\ S &= (n-1)2^n+1 \end{aligned}\] が得られる.
- (B)
- $f(x) = (ax+b)2^{x-1}$ ($a,$ $b$: 実数) とおく. \[\begin{aligned} f(x+1)-f(x) &= \{ a(x+1)+b\} 2^x-(ax+b)2^{x-1} \\ &= 2(ax+a+b)2^{x-1}-(ax+b)2^{x-1} \\ &= \{ 2(ax+a+b)-(ax+b)\} 2^{x-1} \\ &= (ax+2a+b)2^{x-1} \end{aligned}\] であるから, \[\begin{aligned} f(x+1)-f(x) = x2^{x-1} &\iff (ax+2a+b)2^{x-1} = x2^{x-1} \\ &\iff ax+2a+b = x \\ &\iff a = 1,\ b = -2 \end{aligned}\] が成り立つ. このとき $f(x) = (x-2)2^{x-1}$ であるから, \[\begin{aligned} S &= \sum_{k = 1}^n\{ f(k+1)-f(k)\} \\ &= \{ f(n+1)-f(n)\}+\cdots +\{ f(2)-f(1)\} \\ &= f(n+1)-f(1) = (n-1)2^n+1 \end{aligned}\] である.
問題《連続する正の整数の積の和》
$r$ を $2$ 以上の整数, $n$ を正の整数とする.
- (1)
- $x(x+1)\cdots (x+r)-(x-1)x\cdots (x+r-1)$ を因数分解せよ.
- (2)
- \[\sum_{k = 1}^nk(k+1)\cdots (k+r-1) = \frac{1}{r+1}n(n+1)\cdots (n+r)\] が成り立つことを示せ.
解答例
- (1)
- \[\begin{aligned} &x(x+1)\cdots (x+r)-(x-1)x\cdots (x+r-1) \\ &= \{ (x+r)-(x-1)\} x(x+1)\cdots (x+r-1) \\ &= (r+1)x(x+1)\cdots (x+r-1) \end{aligned}\] が成り立つ.
- (2)
- (1) の結果から, \[\begin{aligned} &x(x+1)\cdots (x+r-1) \\ &= \frac{1}{r+1}\{ -(x-1)x\cdots (x+r-1)+x(x+1)\cdots (x+r)\} \end{aligned}\] が成り立つ. $x = 1,$ $\cdots,$ $n$ を代入して辺々を加えると, \[\begin{aligned} &\sum_{k = 1}^nk(k+1)\cdots (k+r-1) \\ &= -\frac{1}{r+1}\{ -0\cdot 1\cdots r+1\cdot 2\cdots (r+1) \\ &\qquad -1\cdot 2\cdots (r+1)+2\cdot 3\cdots (r+2) \\ &\qquad -\cdots \\ &\qquad -(n-1)n\cdots (n+r-1)+n(n+1)\cdots (n+r)\} \\ &= \frac{1}{r+1}n(n+1)\cdots (n+r) \end{aligned}\] が得られる.
参考
- 本問の結果から, \[\sum_{k_r = 1}^n\cdots\sum_{k_1 = 1}^{k_2}k_1 = \frac{1}{(r+1)!}n(n+1)\cdots (n+r) \quad \cdots [1]\] であることが, 数学的帰納法によりわかる.
- $[1]$ は \[\sum_{k_r = 1}^n\cdots\sum_{k_1 = 1}^{k_2}\sum_{k_0 = 1}^{k_1}1 = {}_{n+r}\mathrm C_{r+1} \quad \cdots [2]\] と書き直すこともできる. $[2]$ の左辺の和は, $1 \leqq k_0 \leqq k_1 \leqq k_2 \leqq \cdots \leqq k_r \leqq n$ なる整数の組 $(k_0,k_1,k_2,\cdots,k_r)$ の総数に等しく, $n$ 種類のものから $r+1$ 個とる「重複組合せ」の総数 ${}_n\mathrm H_{r+1} = {}_{n+r}\mathrm C_{r+1}$ に等しいと考えられる.
問題《平方数の逆数の和の評価》
$n$ を正の整数とする.
- (1)
- $n > 1$ のとき, $\dfrac{1}{1\cdot 2}+\dfrac{1}{2\cdot 3}+\cdots +\dfrac{1}{(n-1)n}$ を簡単にせよ.
- (2)
- $n \geqq 1$ のとき, $\dfrac{1}{1^2}+\dfrac{1}{2^2}+\cdots +\dfrac{1}{n^2} < 2$ を示せ.
解答例
- (1)
- \[\frac{1}{(x-1)x} = \frac{1}{x-1}-\frac{1}{x}\] であるから, $n > 1$ のとき \[\begin{aligned} &\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\cdots +\frac{1}{(n-1)n} \\ &= \left(\frac{1}{1}-\frac{1}{2}\right) +\left(\frac{1}{2}-\frac{1}{3}\right) +\cdots +\left(\frac{1}{n-1}-\frac{1}{n}\right) \\ &= 1-\frac{1}{n} \end{aligned}\] である.
- (2)
- (i)
- $n = 1$ のとき. $\dfrac{1}{1^2} = 1 < 2$ である.
- (ii)
- $n > 1$ のとき. (1) の結果から, \[\begin{aligned} \frac{1}{1^2}+\frac{1}{2^2}+\cdots +\frac{1}{n^2} &< 1+\frac{1}{1\cdot 2}+\cdots +\frac{1}{(n-1)n} \\ &= 1+\left( 1-\frac{1}{n}\right) = 2-\frac{1}{n} \\ &< 2 \end{aligned}\] が成り立つ.
参考
- 一般に常に一定値以下の値をとる単調増加数列 (または常に一定値以上の値をとる単調減少数列)は収束するから, 無限級数 $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^2}$ は収束する (関数と極限: 理系). 実際に, $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^2} = \dfrac{\pi ^2}{6} = 1.64493\cdots$ であることが知られている. この値を求める問題は「バーゼル問題」(こちらを参照) と呼ばれる.
- 「汎調和級数」$\displaystyle\sum_{n = 1}^\infty\frac{1}{n^s}$ は, $s > 1$ のとき収束することが知られており (こちらを参照), 定義域を複素数全体に拡げた「リーマン・ゼータ関数」(Riemann zeta function) に一般化される.
問題《立方数の逆数の和の評価》
$n$ を正の整数とする.
- (1)
- $n > 1$ のとき, $\dfrac{1}{1\cdot 2\cdot 3}+\dfrac{1}{2\cdot 3\cdot 4}+\cdots +\dfrac{1}{(n-1)n(n+1)}$ を簡単にせよ.
- (2)
- $n \geqq 1$ のとき, $\dfrac{1}{1^3}+\dfrac{1}{2^3}+\cdots +\dfrac{1}{n^3} < \dfrac{5}{4}$ を示せ.
(参考: $2002$ 一橋大)
解答例
- (1)
- \[\frac{1}{(x-1)x(x+1)} = \frac{1}{2}\left\{\frac{1}{(x-1)x}-\frac{1}{x(x+1)}\right\}\] であるから, $n > 1$ のとき \[\begin{aligned} &\frac{1}{1\cdot 2\cdot 3}+\frac{1}{2\cdot 3\cdot 4}+\cdots +\frac{1}{(n-1)n(n+1)} \\ &= \frac{1}{2}\left(\frac{1}{1\cdot 2}-\frac{1}{2\cdot 3}\right) +\frac{1}{2}\left(\frac{1}{2\cdot 3}-\frac{1}{3\cdot 4}\right) \\ &\qquad +\cdots +\frac{1}{2}\left\{\frac{1}{(n-1)n}-\frac{1}{n(n+1)}\right\} \\ &= \frac{1}{2}\left\{\frac{1}{2}-\frac{1}{n(n+1)}\right\} = \frac{1}{2}\cdot\frac{n(n+1)-2}{2n(n+1)} \\ &= \frac{(n-1)(n+2)}{4n(n+1)} \end{aligned}\] である.
- (2)
- (i)
- $n = 1$ のとき. $\dfrac{1}{1^3} = 1 < \dfrac{5}{4}$ である.
- (ii)
- $n > 1$ のとき. (1) の結果から \[\begin{aligned} &\frac{1}{1^3}+\frac{1}{2^3}+\cdots +\frac{1}{n^3} \\ &< 1+\frac{1}{1\cdot 2\cdot 3}+\cdots +\frac{1}{(n-1)n(n+1)} \\ &= 1+\frac{(n-1)(n+2)}{4n(n+1)} \end{aligned}\] であるので, $\dfrac{(n-1)(n+2)}{4n(n+1)} < \dfrac{1}{4}$ を示せばよい. これは, \[\begin{aligned} \frac{(n-1)(n+2)}{4n(n+1)}-\frac{1}{4} &= \frac{(n-1)(n+2)-n(n+1)}{4n(n+1)} \\ &= \frac{-2}{4n(n+1)} < 0 \end{aligned}\] から従う.
参考
- $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^3} = 1.20205\cdots$ は「アペリーの定数」(Apéry's constant) と呼ばれる.
- $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^s}$ は, $s$ が正の偶数のとき, $s = 3$ のとき無理数であることがオイラー, アペリーによって示されており, 少なくとも無限個の奇数 $s,(\geqq 5)$ に対して無理数であることが知られている.
