関数の極値 (文系・理系共通)
関数の極値
問題《$3$ 次関数のグラフの対称性》
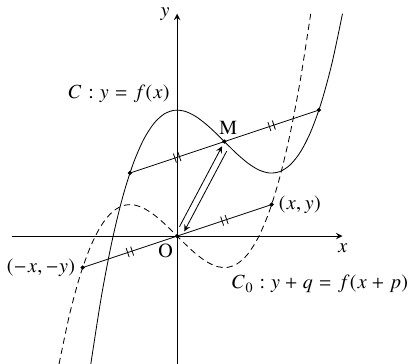
$3$ 次関数 $f(x) = ax^3+bx^2+cx+d$ ($a,$ $b,$ $c,$ $d$: 実数) とそのグラフ $C:y = f(x)$ 上の点 $\mathrm M\left( -\dfrac{b}{3a},f\left( -\dfrac{b}{3a}\right)\right)$ について, 次のことを示せ.
- (A)
- $C$ は点 $\mathrm M$ に関して対称である.
- (B)
- $f(x)$ が $x = \alpha$ で極大値, $x = \beta$ で極小値をとるとする. このとき, $2$ 点 $\mathrm A(\alpha,f(\alpha )),$ $\mathrm B(\beta,f(\beta ))$ を結ぶ線分の中点は $\mathrm M$ と一致する.
解答例
$p = -\dfrac{b}{3a},$ $q = f(p)$ とおく.
- (A)
- $C$ を $x$ 軸方向に $-p,$ $y$ 軸方向に $-q$ だけ平行移動した曲線 $C_0$ の方程式は,
\[ y+q = f(x+p)\]
つまり
\[\begin{aligned}
y &= f(x+p)-q \\
y &= a(x+p)^3+b(x+p)^2+c(x+p)+d-q \\
y &= ax^3+(3ap+b)x^2+(3ap^2+2bp+c)x \\
&\qquad +(ap^3+bp^2+cp+d)-q \\
y &= ax^3+(3ap^2+2bp+c)x
\end{aligned}\]
である.
右辺は $x$ の奇関数であるから, $C_0$ は原点に関して対称である.
$C$ は, $C_0$ を $x$ 軸方向に $p,$ $y$ 軸方向に $q$ だけ平行移動した曲線であるから, 点 $\mathrm M(p,q)$ に関して対称である.
- (B)
- 平行移動しても $2$ 点間の距離は変わらないから, $\mathrm M = \mathrm O$ の場合に \[\frac{\alpha +\beta}{2} = 0 \quad \cdots [1], \quad \frac{f(\alpha )+f(\beta )}{2} = 0 \quad \cdots [2]\] を示せばよい. このとき, $p = 0,$ $f(0) = f(p) = q = 0$ から, $b = d = 0$ で, \[ f(x) = ax^3+cx, \quad f'(x) = 3ax^2+c\] である. 仮定から \[ f'(\alpha ) = f'(\beta ) = 0\] であるので, 解と係数の関係により $\alpha +\beta = 0$ が成り立ち, $[1]$ が従う. さらに, \[\begin{aligned} \frac{f(\alpha )+f(\beta )}{2} &= \frac{a\alpha ^3+c\alpha +a\beta ^3+c\beta}{2} \\ &= \frac{a(\alpha ^3+\beta ^3)+c(\alpha +\beta )}{2} \\ &= \frac{a(\alpha +\beta )(\alpha ^2-\alpha\beta +\beta ^2)+c(\alpha +\beta )}{2} \\ &= 0 \quad \cdots [2] \end{aligned}\] が成り立つ. 以上から, 線分 $\mathrm{AB}$ の中点は $\mathrm M$ と一致する.
参考
- 一般に, 実数値関数 $f(x)$ に対して,
が成り立つ.
$y = f(x)$ が点 $(p,q)$ に関して対称 $\iff$ $y+q = f(x+p)$ が原点に関して対称 $\iff$ $f(-x+p)-q = -f(x+p)+q$ $\iff$ $f(x+p)-q$ が奇関数 - 一般に, 実数値関数 $f(x)$ は偶関数 $\dfrac{f(x)+f(-x)}{2}$ と奇関数 $\dfrac{f(x)-f(-x)}{2}$ の和として \[ f(x) = \frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}\] とただ $1$ 通りに表すことができる. 多項式関数の場合には, 偶関数の部分が偶数次の項の和, 奇関数の部分が奇数次の項の和になる. よって, 多項式関数が偶関数のとき奇数次の項の係数は $0$ であり, 奇関数のとき偶数次の項の係数は $0$ である.
問題《$4$ 次関数のグラフの対称性》
$a,$ $b,$ $c,$ $d,$ $e$ $(a \neq 0)$ を実数とする.
$4$ 次関数 $f(x) = ax^4+bx^3+cx^2+dx+e$ とそのグラフ $C:y = f(x)$ について, 次の問いに答えよ.
- (A)
- $C$ が $y$ 軸に平行な直線 $x = p$ に関して対称であるとする. このとき, $a,$ $b,$ $c,$ $d,$ $e$ を用いて $p$ を表し, $a,$ $b,$ $c,$ $d,$ $e$ の関係式を求めよ.
- (B)
- $f(x)$ がある実数 $x = p$ に関して対称な $2$ 点において等しい極値をとるならば, $C$ は直線 $x = p$ に関して対称であり, $f(x)$ は $x = p$ においても極値をとることを示せ.
解答例
- (A)
- $C$ を $x$ 軸方向に $-p$ だけ平行移動した曲線の方程式は, \[ y = a(x+p)^4+b(x+p)^3+c(x+p)^2+d(x+p)+e\] である. この曲線は $y$ 軸に関して対称であり, 右辺は偶関数であるから, $3$ 次, $1$ 次の項の係数は $0$ であり, \[\begin{aligned} 4ap+b &= 0 \quad \cdots [1], \\ 4ap^3+3bp^2+2cp+d &= 0 \quad \cdots [2] \end{aligned}\] が成り立つ. $[1]$ から, \[ p = -\frac{b}{4a}\] が得られる. これを $[2]$ に代入すると \[\begin{aligned} -\frac{b^3}{16a^2}+\frac{3b^3}{16a^2}-\frac{bc}{2a}+d &= 0 \\ \frac{b^3}{8a^2}-\frac{bc}{2a}+d &= 0 \end{aligned}\] となるから, 求める関係式は \[ b^3-4abc+8a^2d = 0\] である.
- (B)
- 平行移動を考えることにより, $p = 0$ の場合を示せばよい. $f(x)$ が $x = \pm\alpha$ $(\alpha > 0)$ において等しい極値をとるとする. このとき, $f(\alpha ) = f(-\alpha )$ つまり \[ a\alpha ^4+b\alpha ^3+c\alpha ^2+d\alpha +e = a\alpha ^4-b\alpha ^3+c\alpha ^2-d\alpha +e\] であるから, \[\begin{aligned} 2b\alpha ^3+2d\alpha &= 0 \\ b\alpha ^2+d &= 0 \quad \cdots [1] \end{aligned}\] が成り立つ. また, \[ f'(\pm\alpha ) = 0\] であり, \[ f'(x) = 4ax^3+3bx^2+2cx+d\] であるから, \[\begin{aligned} 4a\alpha ^3+3b\alpha ^2+2c\alpha +d &= 0, \quad \cdots [2] \\ -4a\alpha ^3+3b\alpha ^2-2c\alpha +d &= 0 \quad \cdots [3] \end{aligned}\] が成り立つ. $[2]-[3]$ から \[\begin{aligned} 8a\alpha ^3+4c\alpha &= 0 \\ 2a\alpha ^2+c &= 0 \end{aligned}\] が成り立つ. これを $[2]$ つまり \[ 2\alpha (2a\alpha ^2+c)+3b\alpha ^2+d = 0\] に代入すると, \[ 3b\alpha ^2+d = 0 \quad \cdots [4]\] が得られる. よって, $[1],$ $[4]$ から, \[ b = d = 0\] が成り立つ. したがって, $f(x)$ は偶関数であるから, $y = f(x)$ は直線 $x = 0$ に関して対称である. さらに, このとき \[ f'(x) = 4ax^3+2cx = 2x(2ax^2+c)\] であるから, $f'(x) = 0$ は $3$ つの実数解 $x = 0,$ $\pm\alpha$ をもつ. $f'(x)$ の符号は $x = 0,$ $\pm\alpha$ の前後で入れ替わるから, $f(x)$ は $x = 0$ でも極値をとる.
参考
一般に, 実数値関数 $f(x)$ に対して,
が成り立つ.
| $y = f(x)$ が直線 $x = p$ に関して対称 |
| $\iff$ $y = f(x+p)$ が $y$ 軸に関して対称 |
| $\iff$ $f(-x+p) = f(x+p)$ |
| $\iff$ $f(x+p)$ が偶関数 |
