ベクトルと図形
ベクトルの演算
問題《平面ベクトルの線形独立性》
$\vec a = (a_1,a_2),$ $\vec b = (b_1,b_2)$ を平面ベクトルとする.
- (L)
- すべての実数 $s,$ $t$ に対して, \[ s\vec a+t\vec b = \vec 0 \Longrightarrow s = t = 0\] が成り立つ.
- (G)
- $\vec a \neq \vec 0$ かつ $\vec b \neq \vec 0$ かつ $\vec a,$ $\vec b$ は平行でない.
- (B)
- すべての平面ベクトル $\vec p$ は
の形にただ $1$ 通りに表される.$\vec p = s\vec a+t\vec b$ ($s,$ $t$: 実数)
- (1)
- (L), (G) の否定を述べよ. さらに, (L) $\iff$ (G) が成り立つことを示せ.
- (2)
- (G) のとき, 実数 $\alpha,$ $\beta$ に対して, $x,$ $y$ に関する連立方程式 \[\begin{aligned} a_1x+a_2y &= \alpha \quad \cdots [1], \\ b_1x+b_2y &= \beta \quad \cdots [2] \end{aligned}\] は実数解をもつことを示せ. さらに, (G) $\Longrightarrow$ (B) が成り立つことを示せ.
- (3)
- (B) $\Longrightarrow$ (L) が成り立つことを示せ.
解答例
- (1)
- (L), (G) の否定は, それぞれ次の通りである.
- (L) の否定:
- ある実数 $s,$ $t$ に対して, \[ s\vec a+t\vec b = \vec 0, \quad (s,t) \neq (0,0)\] が成り立つ.
- (G) の否定:
- $\vec a,$ $\vec b$ は $\vec 0$ でなければ平行である.
- $\vec a = \vec 0$ のとき. $1\vec a+0\vec b = \vec 0$ が成り立つ.
- $\vec b = \vec 0$ のとき. $0\vec a+1\vec b = \vec 0$ が成り立つ.
- $\vec a,$ $\vec b$ が平行なとき. ある実数 $s$ に対して $\vec b = s\vec a$ が成り立つ. この $s$ と $t = -1$ は $s\vec a+t\vec b = \vec 0$ を満たす.
最後に, (G) $\Longrightarrow$ (L) を対偶法で示すため, (L) の否定を仮定する.- $t = 0$ のとき. $\vec a = \vec 0$ である.
- $t \neq 0$ のとき. $\vec b = -\dfrac{s}{t}\vec a$ が成り立つから, $\vec a,$ $\vec b$ は $\vec 0$ でなければ平行である.
- (2)
- (G) を仮定する.
このとき, $a_1b_2-a_2b_1 \neq 0$ であることに注意すると, $([1]\times b_2-[2]\times a_2)\div (a_1b_2-a_2b_1),$ $([2]\times a_1-[1]\times b_1)\div (a_1b_2-a_2b_1)$ から $[1],$ $[2]$ の実数解
\[\begin{aligned}
x &= s_1\alpha +t_1\beta \quad \left( s_1 = \frac{b_2}{a_1b_2-a_2b_1},\ t_1 = \frac{-a_2}{a_1b_2-a_2b_1}\right), \\
y &= s_2\alpha +t_2\beta \quad \left( s_2 = \frac{-b_1}{a_1b_2-a_2b_1},\ t_2 = \frac{a_1}{a_1b_2-a_2b_1}\right)
\end{aligned}\]
が得られる.
一方, $\vec a,$ $\vec b$ は $\overrightarrow{e_1} = (1,0),$ $\overrightarrow{e_2} = (0,1)$ を用いて
\[\begin{aligned}
a_1\overrightarrow{e_1}+a_2\overrightarrow{e_2} &= \vec a, \\
b_1\overrightarrow{e_1}+b_2\overrightarrow{e_2} &= \vec b
\end{aligned}\]
と表される.
連立方程式 $[1],$ $[2]$ と同様に, これは $\overrightarrow{e_1},$ $\overrightarrow{e_2}$ について解けて
\[\begin{aligned}
\overrightarrow{e_1} &= s_1\vec a+t_1\vec b, \\
\overrightarrow{e_2} &= s_2\vec a+t_2\vec b
\end{aligned}\]
となる.
よって, すべての平面ベクトル $\vec p = (p_1,p_2)$ は
\[\begin{aligned}
\vec p &= p_1\overrightarrow{e_1}+p_2\overrightarrow{e_2} \\
&= p_1(s_1\vec a+t_1\vec b)+p_2(s_2\vec a+t_2\vec b) \\
&= s\vec a+t\vec b \quad \left(\begin{array}{l}
s = p_1s_1+p_2s_2, \\
t = p_1t_1+p_2t_2
\end{array}\right)
\end{aligned}\]
と表される.
とすると, \[\begin{aligned} &s\vec a+t\vec b = s'\vec a+t'\vec b \\ &(s-s')\vec a+(t-t')\vec b = \vec 0 \end{aligned}\] と (G) $\Longrightarrow$ (L) により $s-s' = t-t' = 0$ つまり \[ s = s', \quad t = t'\] となる. ゆえに, (G) $\Longrightarrow$ (B) が成り立つ.$\vec p = s'\vec a+t'\vec b$ ($s',$ $t'$: 実数) - (3)
- $0\vec a+0\vec b = \vec 0$ であるから, (B) $\Longrightarrow$ (L) が成り立つ.
参考
- 「体」(交換法則, 結合法則, 分配法則を満たす四則演算の定義された集合で複数の要素をもつもの) $K$ に対して, 次の条件を満たす集合 $V\,(\neq \varnothing )$ を $K$ 上の「線形空間」または「ベクトル空間」(linear space, vector space) と呼ぶ.
- 交換法則, 結合法則が成り立ち, $0+v = v$ $(v \in V)$ を満たす要素 $0$ と, $V$ の各要素 $v$ に対して $v+(-v) = 0$ を満たす $V$ の要素 $-v$ が存在する.
- 定数倍 $cv$ $(c \in K,\ v \in V)$ が定義されて, \[\begin{aligned} &c(v+w) = cv+cw, \quad (c+d)v = cv+dv, \\ &c(dv) = (cd)v, \quad 1v = v \quad (c,d \in K,\ v,w \in V) \end{aligned}\] が成り立つ.
- $V$ を「体」$K$ 上の「線形空間」とする.
- 条件 (L) について, $V$ に属するベクトル $\overrightarrow{v_1},$ $\cdots,$ $\overrightarrow{v_r}$ は, \[ t_1,\cdots,t_r \in K,\ t_1\overrightarrow{v_1}+\cdots +t_r\overrightarrow{v_r} = \vec 0 \Longrightarrow t_1 = \cdots = t_r = 0\] を満たすとき「線形独立」または「$1$ 次独立」(linearly independent) であるといい, 満たさないとき「線形従属」または「$1$ 次従属」(linearly dependent) であるという.
- 条件 (B) について, $V$ に属するベクトル $\overrightarrow{v_1},$ $\cdots,$ $\overrightarrow{v_n}$ があって $V$ に属するすべてのベクトル $\vec p$ が \[\vec p = t_1\overrightarrow{v_1}+\cdots +t_n\overrightarrow{v_n} \quad (t_1,\cdots,t_n \in K)\] の形にただ $1$ 通りに表されるとき, ベクトルの組 $(\overrightarrow{v_1},\cdots,\overrightarrow{v_n})$ を $V$ の「基底」(basis) と呼び, $V$ の「次元」(dimension) は $n$ であるという. 例えば, 座標平面は $(1,0),$ $(0,1)$ を「基底」にもつから, その「次元」は $2$ である. また, 座標空間は $(1,0,0),$ $(0,1,0),$ $(0,0,1)$ を「基底」にもつから, その「次元」は $3$ である.
- $V$ の「次元」が $n$ であるとき, $V$ に属する「線形独立」なベクトルの個数の最大値は $n$ である.
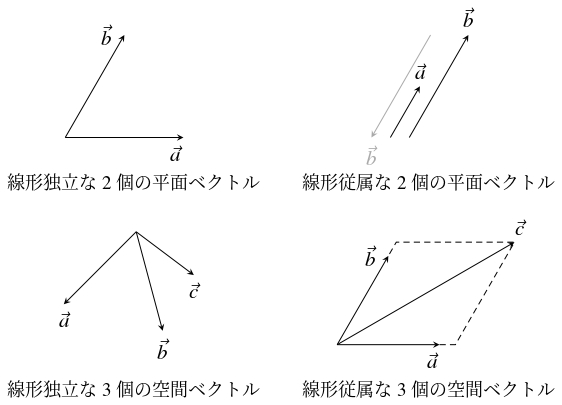
問題《空間ベクトルの線形独立性》
$\vec a = (a_1,a_2,a_3),$ $\vec b = (b_1,b_2,b_3),$ $\vec c = (c_1,c_2,c_3)$ を空間ベクトルとする.
- (L)
- すべての実数 $s,$ $t,$ $u$ に対して, \[ s\vec a+t\vec b+u\vec c = \vec 0 \Longrightarrow s = t = u = 0\] が成り立つ.
- (G)
- $\vec a,$ $\vec b,$ $\vec c$ はいずれも $\vec 0$ でなく, 同一平面上に置けない.
- (B)
- すべての空間ベクトル $\vec p$ は
の形にただ $1$ 通りに表される.$\vec p = s\vec a+t\vec b+u\vec c$ ($s,$ $t,$ $u$: 実数)
- (1)
- (L), (G) の否定を述べよ. さらに, (L) $\iff$ (G) が成り立つことを示せ.
- (2)
- (G) のとき, 実数 $\alpha,$ $\beta,$ $\gamma$ に対して, $x,$ $y,$ $z$ に関する連立方程式 \[\begin{aligned} a_1x+a_2y+a_3z &= \alpha \quad \cdots [1], \\ b_1x+b_2y+b_3z &= \beta \quad \cdots [2], \\ c_1x+c_2y+c_3z &= \gamma \quad \cdots [3] \end{aligned}\] は実数解をもつことが知られている. このことを利用して, (G) $\Longrightarrow$ (B) が成り立つことを示せ.
- (3)
- (B) $\Longrightarrow$ (L) が成り立つことを示せ.
解答例
- (1)
- (L), (G) の否定は, それぞれ次の通りである.
- (L) の否定:
- ある実数 $s,$ $t,$ $u$ に対して, \[ s\vec a+t\vec b+u\vec c = \vec 0, \quad (s,t,u) \neq (0,0,0)\] が成り立つ.
- (G) の否定:
- $\vec a,$ $\vec b,$ $\vec c$ は $\vec 0$ でなければ同一平面上に置ける.
- $\vec a = \vec 0$ のとき. $1\vec a+0\vec b+0\vec c = \vec 0$ が成り立つ.
- $\vec b = \vec 0$ のとき. $0\vec a+1\vec b+0\vec c = \vec 0$ が成り立つ.
- $\vec a,$ $\vec b$ が $\vec 0$ でなく平行なとき. ある実数 $s$ に対して $\vec b = s\vec a$ が成り立つ. この $s$ と $t = -1,$ $u = 0$ は $s\vec a+t\vec b+u\vec c = \vec 0$ を満たす.
- 上記以外のとき. ある実数 $s,$ $t$ に対して $\vec c = s\vec a+t\vec b$ が成り立つ. この $s,$ $t$ と $u = -1$ は $s\vec a+t\vec b+u\vec c = \vec 0$ を満たす.
最後に, (G) $\Longrightarrow$ (L) を対偶法で示すため, (L) の否定を仮定する.- $t = u = 0$ のとき. $\vec a = \vec 0$ である.
- $t \neq 0,$ $u = 0$ のとき. $\vec b = -\dfrac{s}{t}\vec a$ が成り立つから, $\vec a,$ $\vec b$ は $\vec 0$ でなければ平行である.
- $u \neq 0$ のとき. $\vec c = -\dfrac{s}{u}\vec a-\dfrac{t}{u}\vec b$ が成り立つから, $\vec a,$ $\vec b,$ $\vec c$ は $\vec 0$ でなければ同一平面上に置ける.
- (2)
- (G) を仮定する.
$\vec a,$ $\vec b,$ $\vec c$ は $\overrightarrow{e_1} = (1,0,0),$ $\overrightarrow{e_2} = (0,1,0),$ $\overrightarrow{e_3} = (0,0,1)$ を用いて
\[\begin{aligned}
a_1\overrightarrow{e_1}+a_2\overrightarrow{e_2}+a_3\overrightarrow{e_3} &= \vec a, \\
b_1\overrightarrow{e_1}+b_2\overrightarrow{e_2}+b_3\overrightarrow{e_3} &= \vec b, \\
c_1\overrightarrow{e_1}+c_2\overrightarrow{e_2}+b_3\overrightarrow{e_3} &= \vec c
\end{aligned}\]
と表される.
連立方程式 $[1],$ $[2],$ $[3]$ が実数解をもつのと同様に, これは $\overrightarrow{e_1},$ $\overrightarrow{e_2},$ $\overrightarrow{e_3}$ について解けて,
\[\begin{aligned}
\overrightarrow{e_1} &= s_1\vec a+t_1\vec b+u_1\vec c, \\
\overrightarrow{e_2} &= s_2\vec a+t_2\vec b+u_2\vec c, \\
\overrightarrow{e_3} &= s_3\vec a+t_3\vec b+u_3\vec c
\end{aligned}\]
を満たす実数 $s_k,$ $t_k,$ $u_k$ $(1 \leqq k \leqq 3)$ が存在する.
よって, すべての空間ベクトル $\vec p = (p_1,p_2,p_3)$ は
\[\begin{aligned}
\vec p &= p_1\overrightarrow{e_1}+p_2\overrightarrow{e_2}+p_3\overrightarrow{e_3} \\
&= p_1(s_1\vec a+t_1\vec b+u_1\vec c)+p_2(s_2\vec a+t_2\vec b+u_2\vec c) \\
&\qquad +p_3(s_3\vec a+t_3\vec b+u_3\vec c) \\
&= s\vec a+t\vec b+u\vec c \quad \left(\begin{array}{l}
s = p_1s_1+p_2s_2+p_3s_3, \\
t = p_1t_1+p_2t_2+p_3t_3, \\
u = p_1u_1+p_2u_2+p_3u_3
\end{array}\right)
\end{aligned}\]
と表される.
とすると, \[\begin{aligned} &s\vec a+t\vec b+u\vec c = s'\vec a+t'\vec b+u'\vec c \\ &(s-s')\vec a+(t-t')\vec b+(u-u')\vec c = \vec 0 \end{aligned}\] と (G) $\Longrightarrow$ (L) により $s-s' = t-t' = u-u' = 0$ つまり \[ s = s', \quad t = t', \quad u = u'\] となる. ゆえに, (G) $\Longrightarrow$ (B) が成り立つ.$\vec p = s'\vec a+t'\vec b+u'\vec c$ ($s',$ $t',$ $u'$: 実数) - (3)
- $0\vec a+0\vec b+0\vec c = \vec 0$ であるから, (B) $\Longrightarrow$ (L) が成り立つ.
参考
空間ベクトル $(a_1,a_2,a_3),$ $(b_1,b_2,b_3),$ $(c_1,c_2,c_3)$ が「線形独立」であるとき, 実数 $\alpha,$ $\beta,$ $\gamma$ に対して, $x,$ $y,$ $z$ に関する連立方程式
\[\begin{aligned}
a_1x+a_2y+a_3z &= \alpha \quad \cdots [1], \\
b_1x+b_2y+b_3z &= \beta \quad \cdots [2], \\
c_1x+c_2y+c_3z &= \gamma \quad \cdots [3]
\end{aligned}\]
が実数解をもつことは,「行列」の理論を用いて，次のように説明できる (大学で学ぶ内容):
$(a_1,a_2,a_3),$ $(b_1,b_2,b_3),$ $(c_1,c_2,c_3)$ が「線形独立」であるとき,「行列」
\[ A = \begin{pmatrix}
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
c_1 & c_2 & c_3
\end{pmatrix}\]
の「逆行列」$A^{-1}$ が存在するから, 連立方程式 $[1],$ $[2],$ $[3]$ を表す等式
\[ A\begin{pmatrix}
x \\
y \\
z
\end{pmatrix} = \begin{pmatrix}
\alpha \\
\beta \\
\gamma
\end{pmatrix}\]
(左辺は「行列」の積) の左から $A^{-1}$ を掛けることにより
\[\begin{pmatrix}
x \\
y \\
z
\end{pmatrix} = A^{-1}\begin{pmatrix}
\alpha \\
\beta \\
\gamma
\end{pmatrix}\]
が得られる.
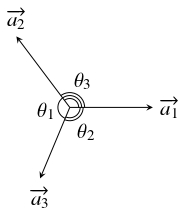
問題《ラミの定理》
$\vec 0$ でないベクトル $\overrightarrow{a_1},$ $\overrightarrow{a_2},$ $\overrightarrow{a_3}$ が同一平面上にあり,
\[\overrightarrow{a_1}+\overrightarrow{a_2}+\overrightarrow{a_3} = \vec 0\]
を満たすとする.
$\overrightarrow{a_2},$ $\overrightarrow{a_3}$ のなす角が $\theta _1,$ $\overrightarrow{a_3},$ $\overrightarrow{a_1}$ のなす角が $\theta _2,$ $\overrightarrow{a_1},$ $\overrightarrow{a_2}$ のなす角が $\theta _3$ であるとき,
\[\frac{|\overrightarrow{a_1}|}{\sin\theta _1} = \frac{|\overrightarrow{a_2}|}{\sin\theta _2} = \frac{|\overrightarrow{a_3}|}{\sin\theta _3}\]
が成り立つことを示せ.
解答例
\[\overrightarrow{\mathrm P_1\mathrm P_2} = \overrightarrow{a_3}, \quad \overrightarrow{\mathrm P_2\mathrm P_3} = \overrightarrow{a_1}, \quad \overrightarrow{\mathrm P_3\mathrm P_4} = \overrightarrow{a_2}\]
とする.
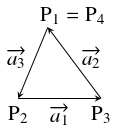このとき,
\[\begin{aligned}
\overrightarrow{\mathrm P_1\mathrm P_4} &= \overrightarrow{\mathrm P_1\mathrm P_2}+\overrightarrow{\mathrm P_2\mathrm P_3}+\overrightarrow{\mathrm P_3\mathrm P_4} \\
&= \overrightarrow{a_3}+\overrightarrow{a_1}+\overrightarrow{a_2} = \vec 0
\end{aligned}\]
が成り立つから, $\mathrm P_1 = \mathrm P_4$ である.
$\triangle\mathrm P_1\mathrm P_2\mathrm P_3$ において $\{ i,j,k\} = \{ 1,2,3\}$ のとき $\angle\mathrm P_k$ の外角は $\overrightarrow{a_i},$ $\overrightarrow{a_j}$ のなす角 $\theta _k$ に等しいから,
\[\angle\mathrm P_k = 180^\circ -\theta _k\]
が成り立つ.
ゆえに, 正弦定理により
\[\frac{|\overrightarrow{a_1}|}{\sin (180^\circ -\theta _1)} = \frac{|\overrightarrow{a_2}|}{\sin (180^\circ -\theta _2)} = \frac{|\overrightarrow{a_3}|}{\sin (180^\circ -\theta _3)}\]
つまり
\[\frac{|\overrightarrow{a_1}|}{\sin\theta _1} = \frac{|\overrightarrow{a_2}|}{\sin\theta _2} = \frac{|\overrightarrow{a_3}|}{\sin\theta _3}\]
が成り立つ.
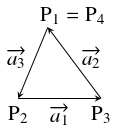
参考
本問の結果は, 「ラミの定理」(Lami's theorem) として知られており, 力学への応用をもつ.
共線条件
問題《メネラウスの定理》
$3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ がそれぞれ $\triangle\mathrm{ABC}$ の $3$ 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の内分点または外分点であり, そのうちの $2$ 個が内分点で $1$ 個が外分点, または $0$ 個が内分点で $3$ 個が外分点であるとして, $\overrightarrow{\mathrm{BP}} = p\overrightarrow{\mathrm{BC}},$ $\overrightarrow{\mathrm{CQ}} = q\overrightarrow{\mathrm{CA}},$ $\overrightarrow{\mathrm{AR}} = r\overrightarrow{\mathrm{AB}}$ ($p,$ $q,$ $r$: $0,$ $1$ でない実数)とする.
さらに, $3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ が同一直線上にあるとして, $\overrightarrow{\mathrm{RP}} = k\overrightarrow{\mathrm{RQ}}$ とする.
また, $\vec b = \overrightarrow{\mathrm{AB}},$ $\vec c = \overrightarrow{\mathrm{AC}}$ とおく.
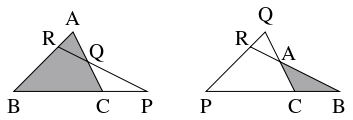
- (1)
- $\vec b,$ $\vec c,$ $p$ を用いて $\overrightarrow{\mathrm{AP}}$ を表せ.
- (2)
- $\vec b,$ $\vec c,$ $k,$ $q,$ $r$ を用いて $\overrightarrow{\mathrm{AP}}$ を表せ.
- (3)
- $p,$ $k$ を用いて $q,$ $r$ を表せ.
- (4)
- $\dfrac{\mathrm{BP}}{\mathrm{PC}}\cdot\dfrac{\mathrm{CQ}}{\mathrm{QA}}\cdot\dfrac{\mathrm{AR}}{\mathrm{RB}} = 1$ が成り立つことを示せ.
解答例
- (1)
- $\overrightarrow{\mathrm{BP}} = p\overrightarrow{\mathrm{BC}} = p(\vec c-\vec b)$ であるから, \[\begin{aligned} \overrightarrow{\mathrm{AP}} &= \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BP}} \\ &= \vec b+p(\vec c-\vec b) \\ &= (1-p)\vec b+p\vec c \quad \cdots [1] \end{aligned}\] である.
- (2)
- $\overrightarrow{\mathrm{RP}} = k\overrightarrow{\mathrm{RQ}} = k(\overrightarrow{\mathrm{AQ}}-\overrightarrow{\mathrm{AR}}),$
$\overrightarrow{\mathrm{AQ}} = \overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CQ}} = \overrightarrow{\mathrm{AC}}+q\overrightarrow{\mathrm{CA}} = (1-q)\vec c$ であるから, \[\begin{aligned} \overrightarrow{\mathrm{AP}} &= \overrightarrow{\mathrm{AR}}+\overrightarrow{\mathrm{RP}} \\ &= \overrightarrow{\mathrm{AR}}+k(\overrightarrow{\mathrm{AQ}}-\overrightarrow{\mathrm{AR}}) \\ &= (1-k)\overrightarrow{\mathrm{AR}}+k\overrightarrow{\mathrm{AQ}} \\ &= (1-k)r\vec b+k(1-q)\vec c \quad \cdots [2] \end{aligned}\] である. - (3)
- $[1],$ $[2]$ から \[ (1-p)\vec b+p\vec c = (1-k)r\vec b+k(1-q)\vec c\] であり, $\vec b,$ $\vec c$ は $\vec 0$ でなく互いに平行でないから, \[ 1-p = (1-k)r, \quad p = k(1-q)\] が成り立つ. これを $q,$ $r$ について解くと \[ q = 1-\frac{p}{k}, \quad r = \frac{1-p}{1-k} \quad \cdots [3]\] が得られる.
- (4)
- $\overrightarrow{\mathrm{PC}} = (1-p)\overrightarrow{\mathrm{BC}},$ $\overrightarrow{\mathrm{QA}} = (1-q)\overrightarrow{\mathrm{CA}},$ $\overrightarrow{\mathrm{RB}} = (1-r)\overrightarrow{\mathrm{AB}}$ であるので, $[3]$ から, \[\begin{aligned} &\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{|\overrightarrow{\mathrm{BP}}|}{|\overrightarrow{\mathrm{PC}}|}\cdot\frac{|\overrightarrow{\mathrm{CQ}}|}{|\overrightarrow{\mathrm{QA}}|}\cdot\frac{|\overrightarrow{\mathrm{AR}}|}{|\overrightarrow{\mathrm{RB}}|} \\ &= \frac{|p||\overrightarrow{\mathrm{BC}}|}{|1-p||\overrightarrow{\mathrm{BC}}|}\cdot\frac{|q||\overrightarrow{\mathrm{CA}}|}{|1-q||\overrightarrow{\mathrm{CA}}|}\cdot\frac{|r||\overrightarrow{\mathrm{AB}}|}{|1-r||\overrightarrow{\mathrm{AB}}|} \\ &= \left|\frac{p}{1-p}\cdot\frac{q}{1-q}\cdot\frac{r}{1-r}\right| = \left|\frac{p}{1-p}\cdot\frac{1-\dfrac{p}{k}}{\dfrac{p}{k}}\cdot\frac{\dfrac{1-p}{1-k}}{1-\dfrac{1-p}{1-k}}\right| \\ &= \left|\frac{p}{1-p}\cdot\frac{k-p}{p}\cdot\frac{1-p}{(1-k)-(1-p)}\right| = |-1| = 1 \end{aligned}\] が成り立つ.
参考
同一直線上にある相異なる $3$ 点 $\mathrm X,$ $\mathrm Y,$ $\mathrm Z$ について,
$\mathrm Z$ が線分 $\mathrm{XY}$ 上にあるとき $\dfrac{\overline{\mathrm{XZ}}}{\overline{\mathrm{ZY}}} = \dfrac{\mathrm{XZ}}{\mathrm{ZY}},$
$\mathrm Z$ が線分 $\mathrm{XY}$ 上にないとき $\dfrac{\overline{\mathrm{XZ}}}{\overline{\mathrm{ZY}}} = -\dfrac{\mathrm{XZ}}{\mathrm{ZY}}$ と定めると,
メネラウスの定理の等式は
\[\frac{\overline{\mathrm{BP}}}{\overline{\mathrm{PC}}}\cdot\frac{\overline{\mathrm{CQ}}}{\overline{\mathrm{QA}}}\cdot\frac{\overline{\mathrm{AR}}}{\overline{\mathrm{RB}}} = -1\]
と精密化できる.
このように向きを含めた線分の長さを「有向長」と呼ぶ.
問題《チェヴァの定理》
$3$ 点 $\mathrm P,$ $\mathrm Q,$ $\mathrm R$ がそれぞれ $\triangle\mathrm{ABC}$ の $3$ 辺 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ の内分点または外分点であり,
そのうちの $3$ 個が内分点で $0$ 個が外分点, または $1$ 個が内分点で $2$ 個が外分点であるとして, $\overrightarrow{\mathrm{BP}} = p\overrightarrow{\mathrm{BC}},$ $\overrightarrow{\mathrm{CQ}} = q\overrightarrow{\mathrm{CA}},$ $\overrightarrow{\mathrm{AR}} = r\overrightarrow{\mathrm{AB}}$ ($p,$ $q,$ $r$: $0,$ $1$ でない実数) とする.
さらに, $3$ 直線 $\mathrm{AP},$ $\mathrm{BQ},$ $\mathrm{CR}$ が $1$ 点 $\mathrm X$ で交わるとして, $\overrightarrow{\mathrm{BX}} = k\overrightarrow{\mathrm{BQ}},$ $\overrightarrow{\mathrm{CX}} = l\overrightarrow{\mathrm{CR}}$ とする.
また, $\vec b = \overrightarrow{\mathrm{AB}},$ $\vec c = \overrightarrow{\mathrm{AC}}$ とおく.
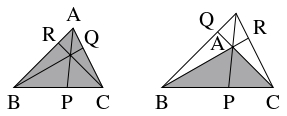
- (1)
- $\vec b,$ $\vec c,$ $k,$ $q$ を用いて $\overrightarrow{\mathrm{AX}}$ を表せ.
- (2)
- $\vec b,$ $\vec c,$ $l,$ $r$ を用いて $\overrightarrow{\mathrm{AX}}$ を表せ.
- (3)
- $q,$ $r$ を用いて $k$ を表せ.
- (4)
- $q,$ $r$ を用いて $p$ を表せ.
- (5)
- $\dfrac{\mathrm{BP}}{\mathrm{PC}}\cdot\dfrac{\mathrm{CQ}}{\mathrm{QA}}\cdot\dfrac{\mathrm{AR}}{\mathrm{RB}} = 1$ が成り立つことを示せ.
解答例
- (1)
- $\overrightarrow{\mathrm{AQ}} = \overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CQ}} = (1-q)\vec c$ であるから, \[\begin{aligned} \overrightarrow{\mathrm{AX}} &= \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BX}} = \overrightarrow{\mathrm{AB}}+k\overrightarrow{\mathrm{BQ}} \\ &= \overrightarrow{\mathrm{AB}}+k(\overrightarrow{\mathrm{AQ}}-\overrightarrow{\mathrm{AB}}) = (1-k)\overrightarrow{\mathrm{AB}}+k\overrightarrow{\mathrm{AQ}} \\ &= (1-k)\vec b+k(1-q)\vec c \quad \cdots [1] \end{aligned}\] である.
- (2)
- $\overrightarrow{\mathrm{AR}} = r\vec b$ であるから, \[\begin{aligned} \overrightarrow{\mathrm{AX}} &= \overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CX}} = \overrightarrow{\mathrm{AC}}+l\overrightarrow{\mathrm{CR}} \\ &= \overrightarrow{\mathrm{AC}}+l(\overrightarrow{\mathrm{AR}}-\overrightarrow{\mathrm{AC}}) = l\overrightarrow{\mathrm{AR}}+(1-l)\overrightarrow{\mathrm{AC}} \\ &= lr\vec b+(1-l)\vec c \quad \cdots [2] \end{aligned}\] である.
- (3)
- $[1],$ $[2]$ から \[ (1-k)\vec b+k(1-q)\vec c = lr\vec b+(1-l)\vec c\] であり, $\vec b,$ $\vec c$ は $\vec 0$ でなく互いに平行でないから, \[ 1-k = lr, \quad k(1-q) = 1-l\] が成り立つ. $l = 1-k(1-q)$ であるから, \[\begin{aligned} 1-k &= r-k(1-q)r \\ k &= \frac{1-r}{1-(1-q)r} \quad \cdots [3] \end{aligned}\] が成り立つ.
- (4)
- $[3]$ を $[1]$ に代入すると, \[\overrightarrow{\mathrm{AX}} = \frac{qr}{1-(1-q)r}\vec b+\frac{(1-q)(1-r)}{1-(1-q)r}\vec c\] が得られる. $\overrightarrow{\mathrm{AP}} = t\overrightarrow{\mathrm{AX}}$ ($t$: 実数) とすると, \[\overrightarrow{\mathrm{AP}} = \frac{qrt}{1-(1-q)r}\vec b+\frac{(1-q)(1-r)t}{1-(1-q)r}\vec c\] となるので, 点 $\mathrm P$ が直線 $\mathrm{BC}$ 上にあることから \[\frac{qrt}{1-(1-q)r}+\frac{(1-q)(1-r)t}{1-(1-q)r} = 1\] よって \[ t = \frac{1-(1-q)r}{qr+(1-q)(1-r)}\] となる. したがって, \[\overrightarrow{\mathrm{AP}} = \frac{qr}{qr+(1-q)(1-r)}\vec b+\frac{(1-q)(1-r)}{qr+(1-q)(1-r)}\vec c\] であり, 点 $\mathrm P$ は辺 $\mathrm{BC}$ を $|(1-q)(1-r)|:|qr|$ に内分または外分するから, \[ p = \frac{qr}{qr+(1-q)(1-r)} \quad \cdots [4]\] が成り立つ.
- (5)
- $\overrightarrow{\mathrm{PC}} = (1-p)\overrightarrow{\mathrm{BC}},$ $\overrightarrow{\mathrm{QA}} = (1-q)\overrightarrow{\mathrm{CA}},$ $\overrightarrow{\mathrm{RB}} = (1-r)\overrightarrow{\mathrm{AB}}$ であるので, $[4]$ から, \[\begin{aligned} &\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}} = \frac{|\overrightarrow{\mathrm{BP}}|}{|\overrightarrow{\mathrm{PC}}|}\cdot\frac{|\overrightarrow{\mathrm{CQ}}|}{|\overrightarrow{\mathrm{QA}}|}\cdot\frac{|\overrightarrow{\mathrm{AR}}|}{|\overrightarrow{\mathrm{RB}}|} \\ &= \frac{|p||\overrightarrow{\mathrm{BC}}|}{|1-p||\overrightarrow{\mathrm{BC}}|}\cdot\frac{|q||\overrightarrow{\mathrm{CA}}|}{|1-q||\overrightarrow{\mathrm{CA}}|}\cdot\frac{|r||\overrightarrow{\mathrm{AB}}|}{|1-r||\overrightarrow{\mathrm{AB}}|} \\ &= \left|\frac{p}{1-p}\cdot\frac{q}{1-q}\cdot\frac{r}{1-r}\right| = \left|\frac{(1-q)(1-r)}{qr}\cdot\frac{q}{1-q}\cdot\frac{r}{1-r}\right| \\ &= |1| = 1 \end{aligned}\] が成り立つ.
参考
同一直線上にある相異なる $3$ 点 $\mathrm X,$ $\mathrm Y,$ $\mathrm Z$ について,
$\mathrm Z$ が線分 $\mathrm{XY}$ 上にあるとき $\dfrac{\overline{\mathrm{XZ}}}{\overline{\mathrm{ZY}}} = \dfrac{\mathrm{XZ}}{\mathrm{ZY}},$
$\mathrm Z$ が線分 $\mathrm{XY}$ 上にないとき $\dfrac{\overline{\mathrm{XZ}}}{\overline{\mathrm{ZY}}} = -\dfrac{\mathrm{XZ}}{\mathrm{ZY}}$ と定めると,
チェヴァの定理の等式は
\[\frac{\overline{\mathrm{BP}}}{\overline{\mathrm{PC}}}\cdot\frac{\overline{\mathrm{CQ}}}{\overline{\mathrm{QA}}}\cdot\frac{\overline{\mathrm{AR}}}{\overline{\mathrm{RB}}} = 1\]
と精密化できる.
このように向きを含めた線分の長さを「有向長」と呼ぶ.
問題《完全四辺形に関するニュートンの定理》
四角形 $\mathrm{ABCD}$ において,
向かい合う $2$ 辺 $\mathrm{AB},$ $\mathrm{CD}$ の延長が点 $\mathrm E$ で交わり,
向かい合う $2$ 辺 $\mathrm{AD},$ $\mathrm{BC}$ の延長が点 $\mathrm F$ で交わるとする.
線分 $\mathrm{AC},$ $\mathrm{BD},$ $\mathrm{EF}$ の中点をそれぞれ $\mathrm L,$ $\mathrm M,$ $\mathrm N$ とおく.
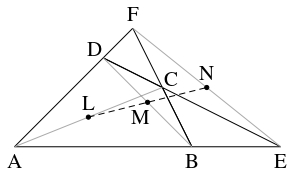
- (1)
- $\overrightarrow{\mathrm{AE}} = s\overrightarrow{\mathrm{AB}},$ $\overrightarrow{\mathrm{AF}} = t\overrightarrow{\mathrm{AD}},$ $\mathrm{BC}:\mathrm{CF} = x:(1-x)$ とおく. $s,$ $t$ を用いて $x$ を表せ.
- (2)
- $3$ 点 $\mathrm L,$ $\mathrm M,$ $\mathrm N$ は同一直線上にあることを示せ.
解答例
- (1)
- $\triangle\mathrm{FAB}$ と直線 $\mathrm{DE}$ にメネラウスの定理を適用すると \[\frac{s}{s-1}\cdot\frac{x}{1-x}\cdot\frac{t-1}{1} = 1\] となるから, これを $x$ について解くと \[ x = \frac{s-1}{st-1}\] が得られる.
- (2)
- $\vec b = \overrightarrow{\mathrm{AB}},$ $\vec d = \overrightarrow{\mathrm{AD}}$ とおく. このとき, (1) の結果から \[\begin{aligned} \overrightarrow{\mathrm{AL}} &= \frac{1}{2}\overrightarrow{\mathrm{AC}} = \frac{1}{2}\{ (1-x)\vec b+xt\vec d\} \\ &= \frac{s(t-1)\vec b+(s-1)t\vec d}{2(st-1)} \quad \left(\because 1-x = \frac{s(t-1)}{st-1}\right) \end{aligned}\] が得られる. また, \[\overrightarrow{\mathrm{AM}} = \frac{\vec b+\vec d}{2}, \quad \overrightarrow{\mathrm{AN}} = \frac{s\vec b+t\vec d}{2}\] であるから, \[\begin{aligned} \overrightarrow{\mathrm{LM}} &= \overrightarrow{\mathrm{AM}}-\overrightarrow{\mathrm{AL}} \\ &= \frac{\vec b+\vec d}{2}-\frac{s(t-1)\vec b+(s-1)t\vec d}{2(st-1)} \\ &= \frac{(s-1)\vec b+(t-1)\vec d}{2(st-1)}, \\ \overrightarrow{\mathrm{MN}} &= \overrightarrow{\mathrm{AN}}-\overrightarrow{\mathrm{AM}} \\ &= \frac{s\vec b+t\vec d}{2}-\frac{\vec b+\vec d}{2} \\ &= \frac{(s-1)\vec b+(t-1)\vec d}{2} \end{aligned}\] が成り立つ. ゆえに, \[\overrightarrow{\mathrm{MN}} = (st-1)\overrightarrow{\mathrm{LM}}\] であるから, $3$ 点 $\mathrm L,$ $\mathrm M,$ $\mathrm N$ は同一直線上にある.
参考
- $4$ 直線とそれらの交点である $6$ 点からなる図形を「完全四辺形」(complete quadrilateral) と呼ぶ.
- 本問の結果は「完全四辺形」に関する「ニュートンの定理」(Newton's theorem) として知られている. 別証明については, こちらを参照されたい.
- 平行四辺形でない四角形において, 対角線の中点を結ぶ直線を「ニュートン線」(Newton line) と呼ぶ.
- 向かい合う辺の中点を結ぶ直線の交点は「ニュートン線」上にあることも知られている.