ヘロンの三角形
ヘロンの公式とヘロンの三角形
定理《ヘロンの公式》
$\triangle\mathrm{ABC}$ において, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB}$ とおき, 半周長 (semiperimeter) を $s = \dfrac{a+b+c}{2}$ とおくと,
\[\triangle\mathrm{ABC} = \sqrt{s(s-a)(s-b)(s-c)}\]
が成り立つ.
証明
こちらを参照.
定義《ヘロンの三角形》
$3$ 辺の長さ $a,$ $b,$ $c$ と面積 $S$ が整数であるような三角形をヘロンの三角形 (Heronian triangle) と呼ぶ.
また, ヘロンの三角形の $3$ 辺の長さの組 $(a,b,c)$ をヘロンの $3$ つ組 (Heronian triple) と呼ぶ.
ヘロンの公式により, これは
\[ S = \frac{1}{4}\sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}\]
が整数となるような三角形の $3$ 辺の長さの組 $(a,b,c)$ に他ならない.
例《ヘロンの三角形》
- (1)
- ピタゴラスの三角形 (こちらを参照), 例えば $3$ 辺の長さが $3,$ $4,$ $5$ である直角三角形は, ヘロンの三角形である.
- (2)
- 合同な $2$ つのピタゴラスの三角形の等辺 (斜辺以外) を貼り合わせて得られる二等辺三角形, 例えば $3$ 辺の長さが $5,$ $5,$ $6$ である三角形はヘロンの三角形である.
- (3)
- $1$ 組の辺 (斜辺以外) の長さが等しく, 合同でない $2$ つのピタゴラスの三角形の等辺を貼り合わせたり,
一方から他方を取り除いたりすることで, ヘロンの三角形を作ることができる.
例えば, $3$ 辺の長さが $9,$ $12,$ $15$ の三角形, $5,$ $12,$ $13$ の三角形において,
長さが $12$ の辺を貼り合わせると $3$ 辺の長さが $13,$ $14,$ $15$ のヘロンの三角形が得られ,
前者から後者を取り除くと $3$ 辺の長さが $4,$ $13,$ $15$ のヘロンの三角形が得られる.
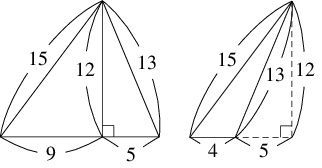
原始的なヘロンの三角形
定義《原始的なヘロンの三角形》
$3$ 辺の長さが $a,$ $b,$ $c$ であるヘロンの三角形, ヘロンの $3$ つ組 $(a,b,c)$ のうち, $a,$ $b,$ $c$ が互いに素であるものは原始的 (primitive) であるという.
ヘロンの三角形を正の整数倍に拡大して得られる三角形はヘロンの三角形である.
次の定理により, 任意のヘロンの三角形は, 原始的なヘロンの三角形 ($3$ 辺の長さの最大公約数の逆数倍に縮小して得られる) の拡大から得られることがわかる.
定理《ヘロンの三角形の縮小》
- (1)
- $3$ 辺の長さが整数, 面積が有理数である三角形はヘロンの三角形である.
- (2)
- ヘロンの三角形を $3$ 辺の長さの正の公約数の逆数倍に縮小して得られる三角形もヘロンの三角形である.
証明
- (1)
- $3$ 辺の長さが整数 $a,$ $b,$ $c,$ 面積が有理数 $S$ である三角形を考える.
ヘロンの公式により,
\[\begin{aligned}
(4S)^2 &= (a+b+c)(b+c-a)(c+a-b)(a+b-c) \\
&= 2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)
\end{aligned}\]
が成り立つ.
- まず, $a+b+c$ は偶数であることを示す.
$a+b+c$ が奇数であるとして, 矛盾を導く.
このとき, $a,$ $b,$ $c$ のうち $1$ つまたは $3$ つが奇数である.
$(4S)^2$ は有理数の $2$ 乗かつ整数であるから, 平方数であることに注意する.
- (i)
- $a,$ $b,$ $c$ のうち $1$ つが奇数であるとき. \[\begin{aligned} &2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4) \\ &\equiv 2(0\cdot 0+0\cdot 1+1\cdot 0)-(0^2+0^2+1^2) \\ &\equiv 3 \pmod 4 \end{aligned}\] となるが, これは $(4S)^2$ が平方数であることに反する.
- (ii)
- $a,$ $b,$ $c$ が奇数であるとき. \[\begin{aligned} &2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4) \\ &\equiv 2(1\cdot 1+1\cdot 1+1\cdot 1)-(1^2+1^2+1^2) \\ &\equiv 3 \pmod 4 \end{aligned}\] となるが, これは $(4S)^2$ が平方数であることに反する.
- $S$ が整数であることを示す. 偶数 $a+b+c$ から $2a,$ $2b,$ $2c$ を引いた $b+c-a,$ $c+a-b,$ $a+b-c$ も偶数であるから, 平方数 $(4S)^2$ は $16$ の倍数である. よって, $S^2$ は整数であるから, $S$ は整数である.
- まず, $a+b+c$ は偶数であることを示す.
$a+b+c$ が奇数であるとして, 矛盾を導く.
このとき, $a,$ $b,$ $c$ のうち $1$ つまたは $3$ つが奇数である.
$(4S)^2$ は有理数の $2$ 乗かつ整数であるから, 平方数であることに注意する.
- (2)
- ヘロンの三角形を $3$ 辺の長さの正の公約数の逆数倍に縮小して得られる三角形は, 面積が有理数であるから, ヘロンの三角形である.
ピタゴラスの三角形との関係
定理《ヘロンの三角形とピタゴラスの三角形の関係》
ピタゴラスの三角形でないすべてのヘロンの三角形は,
ある辺の長さ $c$ について $2c$ のある約数倍 (例えば最も短い辺の長さの $2$ 倍) に拡大すると,
$1$ 組の隣辺を共有する $2$ つのピタゴラスの三角形の和集合または差集合として表せる.
証明
こちらを参照.
ヘロンの三角形の辺の長さの比
定理《ヘロンの三角形の辺の長さの比》
- (1)
- すべてのヘロンの $3$ つ組 $(a,b,c)$ $(a \geqq b \geqq c)$ の比は, \[ mn > h^2 \geqq \frac{m^2n}{2m+n}, \quad m \geqq n\] なる互いに素な正の整数 $m,$ $n,$ $h$ を用いて \[ a:b:c = n(m^2+h^2):m(n^2+h^2):(m+n)(mn-h^2)\] で表される.
- (2)
- $3$ 辺の長さが \[ k\cdot n(m^2+h^2),\ k\cdot m(n^2+h^2),\ k\cdot (m+n)(mn-h^2)\] ($k$: $n(m^2+h^2),$ $m(n^2+h^2),$ $(m+n)(mn-h^2)$ の最大公約数の逆数と正の整数の積) であるヘロンの三角形の面積 $S,$ 周の長さ $L,$ 外接円の半径 $R,$ 内接円の半径 $r$ は \[\begin{aligned} S &= k^2\cdot mnh(m+n)(mn-h^2), \\ L &= k\cdot 2mn(m+n), \\ R &= k\cdot\frac{(m^2+h^2)(n^2+h^2)}{4h}, \\ r &= k\cdot h(mn-h^2) \end{aligned}\] と表される.
証明
- (1)
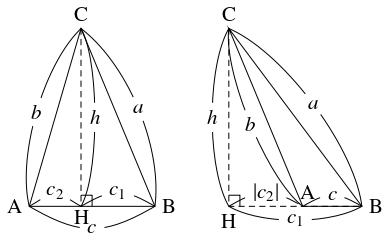
- $\triangle\mathrm{ABC}$ をヘロンの三角形とし, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB}$ $(a \geqq b \geqq c)$ をその辺の長さとする.
上記の定理により, 頂点 $\mathrm C$ から $\mathrm{AB}$ に下ろした垂線の足を $\mathrm H$ とおくと, $h = \mathrm{CH},$ $c_1 = \mathrm{BH},$ $c_2 = c-c_1$ ($c_2 < 0$ を許す) は有理数である.
辺の長さの比を求めるのだから, 必要ならば適当に整数倍して, これらが整数であるとしても一般性を失わない.
整数 $m,$ $n$ を \[ a+c_1 = m, \quad b+c_2 = n\] で定める. このとき, 三平方の定理により, \[ m(a-c_1) = a^2-c_1{}^2 = h^2, \quad n(b-c_2) = b^2-c_2{}^2 = h^2\] が成り立つ. $a > 0,$ $c_1 \geqq 0$ から $m > 0$ であって, $h^2 > 0,$ $b-c_2 > 0$ ($c_2 > 0$ の場合は直角三角形 $\mathrm{ACH}$ の辺の大小関係, $c_2 \leqq 0$ の場合は $b > 0$ から従う) から $n > 0$ であることに注意すると, \[ a-c_1 = \frac{h^2}{m}, \quad b-c_2 = \frac{h^2}{n}\] が得られる. よって, \[\begin{aligned} a &= \frac{1}{2}\left( m+\frac{h^2}{m}\right) = \frac{m^2+h^2}{2m}, \\ b &= \frac{1}{2}\left( n+\frac{h^2}{n}\right) = \frac{n^2+h^2}{2n}, \\ c &= \frac{1}{2}\left( m-\frac{h^2}{m}+n-\frac{h^2}{n}\right) = \frac{(m+n)(mn-h^2)}{2mn} \end{aligned}\] であるから, \[ a:b:c = n(m^2+h^2):m(n^2+h^2):(m+n)(mn-h^2)\] が成り立つ. ここで, $c > 0$ から, $mn > h^2$ である. $b \geqq c$ から, \[ 0 \leqq m(n^2\!+\!h^2)\!-\!(m\!+\!n)(mn\!-\!h^2) = (2m\!+\!n)h^2\!-\!m^2n\] であるので, $h^2 \geqq \dfrac{m^2n}{2m+n}$ が成り立つ. また, $a \geqq b$ から, \[ 0 \leqq n(m^2+h^2)-m(n^2+h^2) = (m-n)(mn-h^2)\] であるので, $mn > h^2$ と合わせると $m \geqq n$ が得られる. さらに, $m,$ $n,$ $h$ の最大公約数を $d$ として $m = dm',$ $n = dn',$ $h = dh'$ とすると, $m',$ $n',$ $h'$ は互いに素な整数になり, \[\begin{aligned} a &= d\cdot\frac{m'{}^2+h'{}^2}{2m'}, \\ b &= d\cdot\frac{n'{}^2+h'{}^2}{2n'}, \\ c &= d\cdot\frac{(m'+n')(m'n'-h'{}^2)}{2m'n'} \end{aligned}\] となるから, $m,$ $n,$ $h$ は互いに素であるように選び直せる.
- (2)
- $a,$ $b,$ $c$ の表示式は (1) から従う. \[\begin{aligned} L &= a+b+c = k\cdot 2mn(m+n), \\ L-2a &= b+c-a = k\cdot 2n(mn-h^2), \\ L-2b &= c+a-b = k\cdot 2m(mn-h^2), \\ L-2c &= a+b-c = k\cdot 2h^2(m+n) \end{aligned}\] であるから, これらの辺々を掛けて正の平方根をとり, $4$ で割ると, ヘロンの公式 \[ S = \frac{1}{4}\sqrt{L(L-2a)(L-2b)(L-2c)}\] により $S$ の表示式が得られる. 外接円の半径 $R,$ 内接円の半径 $r$ は \[ R = \frac{abc}{4S}, \quad r = \frac{2S}{L}\] により, それぞれ求められる.
注意
- $m,$ $n,$ $h$ が互いに素であっても $n(m^2+h^2),$ $m(n^2+h^2),$ $(m+n)(mn-h^2)$ が互いに素であるとは限らず, 等式 \[\begin{aligned} (a,b,c) = (n(m^2+h^2),m(n^2+h^2),(m+n)(mn-h^2)) \\ \left( mn > h^2 \geqq \frac{m^2n}{2m+n},\ m \geqq n\right) \end{aligned}\] で表されない原始的なヘロンの $3$ つ組 $(a,b,c)$ $(a \geqq b \geqq c)$ もある. 例えば, $(m,n,h) = (3,2,2)$ のとき \[\begin{aligned} &(n(m^2+h^2),m(n^2+h^2),(m+n)(mn-h^2)) \\ &= (26,24,10) = 2(13,12,5) \end{aligned}\] であり, $(m+n)(mn-h^2) = 5$ $(mn > h^2)$ は正の整数解をもたないからピタゴラスの $3$ つ組 $(13,12,5)$ はこの等式で表されない.
- $n(m^2+h^2),$ $m(n^2+h^2),$ $(m+n)(mn-h^2)$ に $m,$ $n,$ $h$ の値を代入して, それぞれを最大公約数で割れば, すべての原始的なヘロンの $3$ つ組を生成することができる. $m,$ $n,$ $h$ の取り方は無限にあるから, 原始的なヘロンの $3$ つ組は無限に存在する.
- 原始的なヘロンの $3$ つ組 $(a,b,c)$ $(a \geqq b \geqq c)$ を, 面積 $S$ が小さい順, 周の長さ $L$ が小さい順に, $S \leqq 100$ の範囲で書き出すと, 次のようになる.
上記の比例式で $a,$ $b,$ $c$ の比の値を表す $m,$ $n,$ $h$ の値と, $n(m^2+h^2),$ $m(n^2+h^2),$ $(m+n)(mn-h^2)$ の最大公約数 $g$ の値を付記した.
$\mathrm{PPT}$ と記したものは原始的なピタゴラスの $3$ つ組である.
ピタゴラスの $3$ つ組 $(x_1,y_1,z_1),$ $(x_2,y_2,z_2)$ に対応するピタゴラスの三角形の和集合, 差集合に対応するヘロンの $3$ つ組をそれぞれ $(x_1,y_1,z_1)\cup (x_2,y_2,z_2),$ $(x_1,y_1,z_1)\setminus (x_2,y_2,z_2)$ で表した.
$k(x,y,z) = (kx,ky,kz)$ である.
\[\begin{array}{ccc|cc|cccc|l} a & b & c & S & L & m & n & h & g & \mathrm{Structure} \\ \hline\hline 5 & 4 & 3 & 6 & 12 & 2 & 1 & 1 & 1 & \mathrm{PPT} \\ 6 & 5 & 5 & 12 & 16 & 6 & 4 & 3 & 30 & (3,4,5)\cup (3,4,5) \\ 8 & 5 & 5 & 12 & 18 & 12 & 3 & 4 & 60 & (3,4,5)\cup (3,4,5) \\ 15 & 13 & 4 & 24 & 32 & 6 & 2 & 3 & 6 & 3(3,4,5)\setminus (5,12,13) \\ 13 & 12 & 5 & 30 & 30 & 3 & 2 & 2 & 2 & \mathrm{PPT} \\ 17 & 10 & 9 & 36 & 36 & 8 & 1 & 2 & 4 & (8,15,17)\setminus 2(3,4,5) \\ 26 & 25 & 3 & 36 & 54 & 6 & 3 & 4 & 6 & 2(5,12,13)\setminus (7,24,25) \\ 20 & 15 & 7 & 42 & 42 & 6 & 1 & 2 & 2 & 4(3,4,5)\setminus 3(3,4,5) \\ 13 & 13 & 10 & 60 & 36 & 3 & 3 & 2 & 3 & (5,12,13)\cup (5,12,13) \\ 17 & 15 & 8 & 60 & 40 & 5 & 3 & 3 & 6 & \mathrm{PPT} \\ 24 & 13 & 13 & 60 & 50 & 60 & 5 & 12 & 780 & (5,12,13)\cup (5,12,13) \\ 29 & 25 & 6 & 60 & 60 & 5 & 1 & 2 & 1 & (20,21,29)\setminus 5(3,4,5) \\ 20 & 13 & 11 & 66 & 44 & 9 & 2 & 3 & 9 & 4(3,4,5)\setminus (5,12,13) \\ 30 & 29 & 5 & 72 & 64 & 12 & 8 & 9 & 60 & {} \\ 15 & 14 & 13 & 84 & 42 & 7 & 6 & 4 & 26 & 3(3,4,5)\cup (5,12,13) \\ 21 & 17 & 10 & 84 & 48 & 14 & 6 & 7 & 70 & 2(3,4,5)\cup (8,15,17) \\ 25 & 24 & 7 & 84 & 56 & 4 & 3 & 3 & 3 & \mathrm{PPT} \\ 35 & 29 & 8 & 84 & 72 & 21 & 3 & 7 & 42 & 7(3,4,5)\setminus (20,21,29) \\ 25 & 17 & 12 & 90 & 54 & 15 & 3 & 5 & 30 & 5(3,4,5)\setminus (8,15,17) \\ 53 & 51 & 4 & 90 & 108 & 9 & 3 & 5 & 6 & (28,45,53)\setminus 3(8,15,17) \end{array}\] $3$ 辺の長さが $30,$ $29,$ $5$ であるヘロンの三角形は, どの辺を底辺としても高さが整数にならないから, $2$ つのピタゴラスの三角形の和集合, 差集合として表せない.
ヘロンの三角形の性質
定理《ヘロンの三角形の性質》
- (1)
- ヘロンの三角形の周の長さは偶数である.
- (2)
- ヘロンの三角形の面積は $6$ の倍数である.
証明
$3$ 辺の長さが整数 $a,$ $b,$ $c$ である三角形の面積を $S$ とおき, $s = \dfrac{a+b+c}{2}$ とおく.
ヘロンの公式により,
\[\begin{aligned}
S^2 &= s(s-a)(s-b)(s-c) \quad \cdots [1] \\
(4S)^2 &= (a+b+c)(b+c-a)(c+a-b)(a+b-c) \quad \cdots [2]
\end{aligned}\]
が成り立つ.
- (1)
- 既に示した定理から従うが, より手短な証明を与えておく.
$a+b+c$ が奇数であるならば, $a+b+c$ から $2a,$ $2b,$ $2c$ を引いた $b+c-a,$ $c+a-b,$ $a+b-c$ も奇数であるから, $[2]$ により $(4S)^2$ は奇数であり, よって $S$ は整数でない.
ゆえに, ヘロンの三角形の周の長さは偶数である. - (2)
- $S$ が整数であるとする.
$a,$ $b,$ $c$ が互いに素である場合に, $S$ が偶数かつ $3$ の倍数であることを示せば十分である.
- $S$ が偶数であること: (1) により $a+b+c$ は偶数であり, $s$ は整数で, $a,$ $b,$ $c$ のうち $1$ つは偶数, $2$ つは奇数である. よって, $s-a,$ $s-b,$ $s-c$ は整数で, そのうち少なくとも $1$ つは偶数である. $[1]$ により $S^2$ は偶数であるから, $S$ は偶数である.
- $S$ が $3$ の倍数であること:
\[\begin{aligned}
s &= 3s-2s = 3s-(a+b+c) \\
&= (s-a)+(s-b)+(s-c) \quad \cdots [3]
\end{aligned}\]
であることに注意する.
- (i)
- $s-a,$ $s-b,$ $s-b$ の少なくとも $1$ つが $3$ の倍数であるとき. $[1]$ により, $S^2$ は $3$ の倍数であるから, $S$ は $3$ の倍数である.
- (ii)
- $s-a \equiv s-b \equiv s-c \pmod 3$ のとき. $[3]$ により \[\begin{aligned} s \equiv 3(s-a) \equiv 0 \pmod 3 \end{aligned}\] であるから, $[1]$ により $S^2$ は $3$ の倍数であり, よって $S$ は $3$ の倍数である.
- (iii)
- $s-a,$ $s-b,$ $s-c$ を $3$ で割った余りの $2$ つが $1,$ $1$ つが $2$ であるとき. $[3]$ により \[ s \equiv 1+1+2 \equiv 1 \pmod 3\] であるから, $[1]$ により \[ S^2 \equiv 1\cdot 1\cdot 1\cdot 2 = 2 \pmod 3\] である. 平方数を $3$ で割った余りは $0$ または $1$ であるから, これは矛盾である.
- (iv)
- $s-a,$ $s-b,$ $s-c$ を $3$ で割った余りの $1$ つが $1,$ $2$ つが $2$ であるとき. $[3]$ により \[ s \equiv 1+2+2 \equiv 2 \pmod 3\] であるから, $[1]$ により \[ S^2 \equiv 2\cdot 1\cdot 2\cdot 2 \equiv 2 \pmod 3\] である. 平方数を $3$ で割った余りは $0$ または $1$ であるから, これは矛盾である.
高校数学の問題
図形と計量
問題《ヘロンの三角形》
$\triangle\mathrm{ABC}$ の頂点 $\mathrm C$ から $\mathrm{AB}$ に下ろした垂線の足を $\mathrm H$ とおく.
- (1)
- $a,$ $b,$ $c$ と $S = \triangle\mathrm{ABC}$ を用いて, $\dfrac{\mathrm{AH}}{b},$ $\dfrac{\mathrm{BH}}{a},$ $\dfrac{\mathrm{CH}}{b}$ を表せ.
- (2)
- $a,$ $b,$ $c$ と $S$ が整数であるならば, $2c\cdot\mathrm{AH},$ $2c\cdot\mathrm{BH},$ $c\cdot\mathrm{CH}$ は整数であることを示せ.
解答例
こちらを参照.
問題《ヘロンの公式とブラーマグプタの三角形》
次のことを示せ.
- (1)
- $\triangle\mathrm{ABC}$ において, 周の半分の長さを $s$ とおく.
このとき,
\[\triangle\mathrm{ABC} = \sqrt{s(s-a)(s-b)(s-c)}\]
が成り立つ.
(参考: $2010$ 大阪教育大,$2019$ 京都府立大ほか)
- (2)
- $3$ 辺の長さが $b-1,$ $b,$ $b+1$ である三角形の面積 $S$ が整数であるとする. このとき, $b$ は偶数であり, $x = \dfrac{b}{2}$ とおくと, ある正の整数 $y$ に対して $x^2-3y^2 = 1$ となる.
解答例
こちらを参照.