定積分の不等式
定積分の不等式
定理《積分の単調性》
閉区間 $[a,b]$ において連続な関数 $f(x),$ $g(x)$ が $f(x) \geqq g(x)$ を満たすならば,
\[\int_a^bf(x)\,dx \geqq \int_a^bg(x)\,dx\]
が成り立つ.
定理《積分の三角不等式》
閉区間 $[a,b]$ において連続な関数 $f(x)$ に対して
\[\left|\int_a^bf(x)\,dx\right| \leqq \int_a^b|f(x)|\,dx\]
が成り立つ.
証明
\[ -|f(x)| \leqq f(x) \leqq |f(x)|\]
であるから, 積分の単調性により
\[ -\int_a^b|f(x)|\,dx = \int_a^b\{ -|f(x)|\}\,dx \leqq \int_a^bf(x)\,dx \leqq \int_a^b|f(x)|\,dx\]
つまり
\[\left|\int_a^bf(x)\,dx\right| \leqq \int_a^b|f(x)|\,dx\]
が成り立つ.
問題《積分の平均値の定理》
関数 $f(x)$ が閉区間 $[a,b]$ で連続であるとする.
このとき,
\[\frac{1}{b-a}\int_a^bf(x)\,dx = f(c), \quad a < c < b\]
を満たす実数 $c$ が少なくとも $1$ つ存在することを示せ.
(参考: $1999$ 京都大)
解答例
- (i)
- $f(x) = k$ (定数関数) のとき. $a < c < b$ なる任意の実数 $c$ に対して \[\frac{1}{b-a}\int_a^bf(x)\,dx = \frac{1}{b-a}[kx]_a^b = k = f(c)\] が成り立つ.
- (ii)
- $f(x)$ が定数関数でないとき. $f(x)$ は $a \leqq x \leqq b$ における連続関数であるから, 最大値 $M,$ 最小値 $m$ をもつ. \[ m \leqq f(x) \leqq M\] であり, 等号は常に成り立たないから, 各辺を $a$ から $b$ まで積分すると, \[\begin{aligned} \int_a^b m\,dx < &\int_a^bf(x)\,dx < \int_a^bM\,dx \\ m(b-a) < &\int_a^bf(x)\,dx < M(b-a) \\ m < &\frac{1}{b-a}\int_a^bf(x)\,dx < M \end{aligned}\] が得られる. 中間値の定理により, 最大値, 最小値を与える $x$ の値の間に \[ f(c) = \frac{1}{b-a}\int_a^bf(x)\,dx\] を満たす実数 $c$ が存在する.
別解: (微分の) 平均値の定理を利用
$m = \dfrac{a+b}{2}$ とおく.
関数 $F(x) = \displaystyle\int_m^xf(t)\,dt$ $(a \leqq x \leqq b)$ に平均値の定理を適用すると, $a < c < b$ なるある実数 $c$ に対して
\[\frac{F(b)-F(a)}{b-a} = F'(c)\]
つまり
\[\begin{aligned}
f(c) &= \frac{1}{b-a}\left\{\int_m^bf(t)\,dt-\int_m^af(t)\,dt\right\} \\
&= \frac{1}{b-a}\left\{\int_a^mf(x)\,dx+\int_m^bf(x)\,dx\right\} = \frac{1}{b-a}\int_a^bf(x)\,dx
\end{aligned}\]
が得られる.
参考
$[a,b]$ を含む開区間で $f(x)$ が微分可能で $f'(x)$ が連続であるとき, $f'(x)$ に本問で示した「積分の平均値の定理」(mean value theorem for integrals) を適用すると, (微分の) 平均値の定理が得られる.
問題《定積分のコーシー=シュワルツの不等式》
$a \leqq x \leqq b$ で定義された連続関数 $f(x),$ $g(x)$ について, $\{tf(x)+g(x)\} ^2$ ($t$: 実数) の定積分を考えることで,
\[\left\{\int_a^bf(x)g(x)\,dx\right\} ^2 \leqq \int_a^bf(x)^2\,dx\int_a^bg(x)^2\,dx\]
が成り立つことを示せ.
解答例
- (i)
- 関数として $f(x) \neq 0$ のとき. $t$ を任意の実数とする. $\{tf(x)+g(x)\} ^2 \geqq 0$ から, \[\begin{aligned} &\int_a^b\{tf(x)+g(x)\} ^2\,dx \geqq 0 \\ &t^2\int_a^bf(x)^2\,dx\!+\!2t\int_a^bf(x)g(x)\,dx\!+\!\int_a^bg(x)^2\,dx \!\geqq\! 0 \end{aligned}\] が成り立つ. $t$ の $2$ 次方程式 $(\text{左辺}) = 0$ の判別式が $0$ 以下であることから, \[\begin{aligned} &\left\{\int_a^bf(x)g(x)\,dx\right\} ^2-\int_a^bf(x)^2\,dx\int_a^bg(x)^2\,dx \leqq 0 \\ &\left\{\int_a^bf(x)g(x)\,dx\right\} ^2 \leqq \int_a^bf(x)^2\,dx\int_a^bg(x)^2\,dx \end{aligned}\] が成り立つ.
- (ii)
- 関数として $f(x) = 0$ のとき. この不等式は両辺が $0$ となって成り立つ.
参考
- 解析学において, 関数をベクトルのように扱い, 連続関数 $f(x),$ $g(x)$ $(a \leqq x \leqq b)$ の「内積」$\langle f,g\rangle$ を定積分 \[\langle f,g\rangle = \int_a^bf(x)g(x)\,dx\] で定義する.
- 「体」(交換法則, 結合法則, 分配法則を満たす四則演算の定義された集合で複数の要素をもつもの) $K$ に対して, 次の条件を満たす集合 $V\,(\neq \varnothing )$ を $K$ 上の「線形空間」または「ベクトル空間」(linear space, vector space) と呼ぶ.
- 交換法則, 結合法則が成り立ち, $0+v = v$ $(v \in V)$ を満たす要素 $0$ と, $V$ の各要素 $v$ に対して $v+(-v) = 0$ を満たす $V$ の要素 $-v$ が存在する.
- 定数倍 $cv$ $(c \in K,\ v \in V)$ が定義されて, \[\begin{aligned} &c(v+w) = cv+cw, \quad (c+d)v = cv+dv, \\ &c(dv) = (cd)v, \quad 1v = v \quad (c,d \in K,\ v,w \in V) \end{aligned}\] が成り立つ.
- 実数全体の集合を $\mathbb R$ で表す.
$\mathbb R$ 上の「ベクトル空間」$V$ の要素の対 $(v,w)$ を実数 $\langle v,w\rangle$ に移す対応で, 次の条件を満たすものを $V$ の「内積」(inner product) と呼ぶ.
- $\langle v,w\rangle = \langle w,v\rangle$ $(v,w \in V)$ が成り立つ.
- $\langle cv+v',w\rangle = c\langle v,w\rangle +\langle v',w\rangle$ $(c \in \mathbb R,\ v,v',w \in V)$ が成り立つ.
- $\langle v,v\rangle \geqq 0$ $(v \in V)$ であり, 等号成立は $v = 0$ の場合に限る.
- $\mathbb R$ 上の「ベクトル空間」$V$ の「内積」$\langle v,w\rangle$ に対して,「コーシー=シュワルツの不等式」(Cauchy–Schwarz inequality)
\[\langle v,w\rangle ^2 \leqq \langle v,v\rangle\langle w,w\rangle \quad (v,w \in V)\]
が成り立つ.
$n$ 個の実数の組全体のなす「ベクトル空間」において $n$ 変数の不等式が成り立ち (こちらを参照), 実数値連続関数のなす「ベクトル空間」において本問の不等式が成り立つ.
証明は, 上記の問題とまったく同様である.
- (i)
- $v \neq 0$ のとき. $t$ を任意の実数とする. \[\begin{aligned} \langle tv+w,tv+w\rangle &\geqq 0 \\ t^2\langle v,v\rangle +2t\langle v,w\rangle +\langle w,w\rangle &\geqq 0 \end{aligned}\] が成り立つ. $t$ の $2$ 次方程式 $(\text{左辺}) = 0$ の判別式が $0$ 以下であることから, \[\begin{aligned} &\langle v,w\rangle ^2-\langle v,v\rangle\langle w,w\rangle \leqq 0 \\ &\langle v,w\rangle ^2 \leqq \langle v,v\rangle\langle w,w\rangle \end{aligned}\] が成り立つ.
- (ii)
- $v = 0$ のとき. この不等式は両辺が $0$ となって成り立つ.
問題《指数関数のマクローリン展開にまつわる不等式》
$n$ を非負整数とする.
$x \geqq 0$ において
\[ e^x \geqq \sum_{k = 0}^n\frac{x^k}{k!} \quad \cdots [*]\]
が成り立つことを, 定積分の単調性
\[ f(t) \leqq g(t) \Longrightarrow \int_a^bf(t)\,dt \leqq \int_a^bg(t)\,dt\]
を使って示せ.
(参考: $2022$ 浜松医科大, $2021$ 室蘭工業大, $2013$ 同志社大ほか)
解答例
- (i)
- $n = 0$ のとき. \[ e^x \geqq 1 = \frac{x^0}{0!}\] であるから, $[*]$ が成り立つ.
- (ii)
- $n = m$ ($m$: 非負整数) のとき $[*]$ が成り立つとする. このとき, $e^t \geqq \displaystyle\sum_{k = 0}^m\frac{t^k}{k!}$ の両辺を $0$ から $x$ まで積分すると, \[\begin{aligned} \int_0^xe^t\,dt &\geqq \int_0^x\sum_{k = 0}^m\frac{t^k}{k!}\,dt = \sum_{k = 0}^m\int_0^x\frac{t^k}{k!}\,dt \\ [e^t]_0^x &\geqq \sum_{k = 0}^m\left[\frac{t^{k+1}}{(k+1)!}\right] _0^x \\ e^x-1 &\geqq \sum_{k = 0}^m\frac{x^{k+1}}{(k+1)!} = \sum_{k = 1}^{m+1}\frac{x^k}{k!} \\ e^x &\geqq 1+\sum_{k = 1}^{m+1}\frac{x^k}{k!} = \sum_{k = 0}^{m+1}\frac{x^k}{k!} \end{aligned}\] となり, $n = m+1$ のとき $[*]$ が成り立つ.
参考
指数関数は
\[ e^x = \sum_{n = 0}^\infty\frac{x^n}{n!}\]
と「マクローリン展開」(こちらを参照) される.
問題《対数関数のテイラー展開にまつわる不等式》
$m$ を正の整数, $0 \leqq x < 1$ とする.
次のことを示せ.
- (1)
- \[\sum_{n = 0}^\infty (-x)^n = \frac{1}{1+x}\] である.
- (2)
- \[\sum_{k = 0}^{2m-1}(-x)^k \leqq \frac{1}{1+x} \leqq \sum_{k = 0}^{2m}(-x)^k\] が成り立つ.
- (3)
- \[\sum_{k = 1}^{2m}\frac{(-1)^{k-1}}{k}x^k \leqq \log (1+x) \leqq \sum_{k = 1}^{2m+1}\frac{(-1)^{k-1}}{k}x^k\] が成り立つ.
(参考: $2022$ 信州大)
解答例
- (1)
- $0 \leqq x < 1$ であるから, 無限等比級数の和の公式により, \[\sum_{n = 0}^\infty (-x)^n = \frac{1}{1-(-x)} = \frac{1}{1+x}\] である.
- (2)
- (1) により \[\begin{aligned} &\sum_{k = 0}^{2m}(-x)^k-\frac{1}{1+x} = \sum_{k = 0}^{2m}(-x)^k-\sum_{n = 0}^\infty (-x)^n \\ &= -\sum_{n = 2m+1}^\infty (-x)^n = -\frac{(-x)^{2m+1}}{1-(-x)} = \frac{x^{2m+1}}{1+x} \geqq 0, \\ &\frac{1}{1+x}-\sum_{k = 0}^{2m-1}(-x)^k = \sum_{n = 0}^\infty (-x)^n-\sum_{k = 0}^{2m-1}(-x)^k \\ &= \sum_{n = 2m}^\infty (-x)^n = \frac{(-x)^{2m}}{1-(-x)} = \frac{x^{2m}}{1+x} \geqq 0 \end{aligned}\] であるから, \[\sum_{k = 0}^{2m-1}(-x)^k \leqq \frac{1}{1+x} \leqq \sum_{k = 0}^{2m}(-x)^k\] が成り立つ.
- (3)
- (2) により, \[\begin{aligned} \int_0^x\sum_{k = 0}^{2m-1}(-t)^k\,dt &\leqq \int_0^x\frac{dt}{1+t} \leqq \int_0^x\sum_{k = 0}^{2m}(-t)^k\,dt \\ \sum_{k = 0}^{2m-1}(-1)^k\int_0^xt^k\,dt &\leqq \int_0^x\frac{dt}{1+t} \leqq \sum_{k = 0}^{2m}(-1)^k\int_0^xt^k\,dt \\ \sum_{k = 0}^{2m-1}(-1)^k\!\left[\frac{t^{k+1}}{k\!+\!1}\right] _0^x &\leqq [\log (1+t)]_0^x \leqq \sum_{k = 0}^{2m}(-1)^k\!\left[\frac{t^{k+1}}{k\!+\!1}\right] _0^x \\ \sum_{k = 0}^{2m-1}\frac{(-1)^k}{k+1}x^{k+1} &\leqq \log (1+x) \leqq \sum_{k = 0}^{2m}\frac{(-1)^k}{k+1}x^{k+1} \\ \sum_{k = 1}^{2m}\frac{(-1)^{k-1}}{k}x^k &\leqq \log (1+x) \leqq \sum_{k = 1}^{2m+1}\frac{(-1)^{k-1}}{k}x^k \end{aligned}\] が成り立つ.
参考
対数関数は
\[\log (1+x) = \sum_{n = 1}^\infty\frac{(-1)^{n-1}}{n}x^n \quad (-1 < x \leqq 1)\]
と「テイラー展開」(こちらを参照) される.
問題《逆双曲線関数のテイラー展開にまつわる不等式》
$n$ を正の整数, $0 \leqq x < 1$ とする.
次のことを示せ.
- (1)
- \[\sum_{n = 0}^\infty x^{2n} = \frac{1}{1-x^2}\] である.
- (2)
- \[\frac{1}{1-x^2} \geqq \sum_{k = 0}^nx^{2k}\] が成り立つ.
- (3)
- \[\frac{1}{2}\log\frac{1+x}{1-x} \geqq \sum_{k = 0}^n\frac{1}{2k+1}x^{2k+1}\] が成り立つ.
解答例
- (1)
- $0 \leqq x < 1$ であるから, 無限等比級数の和の公式により, \[\sum_{n = 0}^\infty x^{2n} = \frac{1}{1-x^2}\] である.
- (2)
- (1) により \[\begin{aligned} &\frac{1}{1-x^2}-\sum_{k = 0}^nx^{2k} = \sum_{k = 0}^\infty x^{2k}-\sum_{k = 0}^nx^{2k} \\ &= \sum_{k = n+1}^\infty x^{2k} = \frac{x^{2n+2}}{1-x^2} \geqq 0 \end{aligned}\] であるから, \[\frac{1}{1-x^2} \geqq \sum_{k = 0}^nx^{2k}\] が成り立つ.
- (3)
- (2) により, \[\begin{aligned} \int_0^x\frac{dt}{1-t^2} &\geqq \int_0^x\sum_{k = 0}^nt^{2k}\,dt \\ \int_0^x\frac{1}{2}\left(\frac{1}{1+t}+\frac{1}{1-t}\right)\,dt &\geqq \sum_{k = 0}^n\int_0^xt^{2k}\,dt \\ \frac{1}{2}[\log (1+t)-\log (1-t)]_0^x &\geqq \sum_{k = 0}^n\left[\frac{t^{2k+1}}{2k+1}\right] _0^x \\ \frac{1}{2}\log\frac{1+x}{1-x} &\geqq \sum_{k = 0}^n\frac{1}{2k+1}x^{2k+1} \end{aligned}\] が成り立つ.
参考
- 「双曲線関数」の $1$ つ $\mathop{\mathrm{tanh}}x = \dfrac{e^x-e^{-x}}{e^x+e^{-x}}$ の逆関数は, $\dfrac{1}{2}\log\dfrac{1+x}{1-x}$ であり, $\mathop{\mathrm{artanh}}x$ で表される.
- $\mathop{\mathrm{artanh}}x$ は \[\mathop{\mathrm{artanh}}x = \sum_{n = 0}^\infty\frac{1}{2n+1}x^{2n+1} \quad (-1 < x < 1)\] と「テイラー展開」(こちらを参照) される. この公式は, 対数の近似値の計算に有用である.
問題《三角関数のマクローリン展開にまつわる不等式》
$n$ を正の整数とする.
$x \geqq 0$ において
\[\begin{aligned}
\sum_{k = 0}^{2n+1}\frac{(-1)^k}{(2k)!}x^{2k} &\leqq \cos x \leqq \sum_{k = 0}^{2n}\frac{(-1)^k}{(2k)!}x^{2k}, \\
\sum_{k = 0}^{2n+1}\frac{(-1)^k}{(2k+1)!}x^{2k+1} &\leqq \sin x \leqq \sum_{k = 0}^{2n}\frac{(-1)^k}{(2k+1)!}x^{2k+1}
\end{aligned}\]
が成り立つことを, 定積分の単調性
\[ f(t) \leqq g(t) \Longrightarrow \int_a^bf(t)\,dt \leqq \int_a^bg(t)\,dt\]
を使って示せ.
解答例
- (i)
- $n = 1$ のとき. $x \geqq 0$ とする. $\cos t \leqq 1$ の両辺を $0$ から $x$ まで積分すると, \[\sin x \leqq x\] が得られる. $\sin t \leqq t$ の両辺を $0$ から $x$ まで積分すると, \[\begin{aligned} -\cos x+1 &\leqq \frac{1}{2}x^2 \\ 1-\frac{1}{2}x^2 &\leqq \cos x \end{aligned}\] が得られる. $1-\dfrac{1}{2}t^2 \leqq \cos t$ の両辺を $0$ から $x$ まで積分すると, \[ x-\frac{1}{6}x^3 \leqq \sin x\] が得られる.
- (ii)
- 与えられた正の整数 $n$ に対して不等式が成り立つとし, $x \geqq 0$ とする. $\displaystyle\sum_{k = 0}^{2n+1}\frac{(-1)^k}{(2k+1)!}t^{2k+1} \leqq \sin t$ の両辺を $0$ から $x$ まで積分すると, \[\begin{aligned} \sum_{k = 0}^{2n+1}\frac{(-1)^k}{(2k+2)!}x^{2k+2} &\leqq -\cos x+1 \\ \cos x &\leqq \sum_{k = 0}^{2n+2}\frac{(-1)^k}{(2k)!}x^{2k} \end{aligned}\] が得られる. $\cos t \leqq \displaystyle\sum_{k = 0}^{2n+2}\frac{(-1)^k}{(2k)!}t^{2k}$ の両辺を $0$ から $x$ まで積分すると, \[\sin x \leqq \sum_{k = 0}^{2n+2}\frac{(-1)^k}{(2k+1)!}x^{2k+1}\] が得られる. $\sin t \leqq \displaystyle\sum_{k = 0}^{2n+2}\frac{(-1)^k}{(2k+1)!}t^{2k+1}$ の両辺を $0$ から $x$ まで積分すると, \[\begin{aligned} -\cos x+1 &\leqq \sum_{k = 0}^{2n+2}\frac{(-1)^k}{(2k+2)!}x^{2k+2} \\ \sum_{k = 0}^{2n+3}\frac{(-1)^k}{(2k)!}x^{2k} &\leqq \cos x \end{aligned}\] が得られる. $\displaystyle\sum_{k = 0}^{2n+3}\frac{(-1)^k}{(2k)!}t^{2k} \leqq \cos t$ の両辺を $0$ から $x$ まで積分すると, \[\sum_{k = 0}^{2n+3}\frac{(-1)^k}{(2k+1)!}x^{2k+1} \leqq \sin x\] が得られる.
問題《グレゴリー=ライプニッツ級数》
各正の整数 $n$ に対して関数 $f_n(t)$ を
\[ f_n(t) = \frac{1}{1+t^2}-\sum_{k = 0}^{n-1}(-t^2)^k\]
で定め, $\tan\theta\ \left( -\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\right)$ の逆関数を $\arctan x$ で表す.
次のことを示せ.
- (1)
- $f_n(t) = \dfrac{(-t^2)^n}{1+t^2}$ である.
- (2)
- $0 \leqq x \leqq 1$ のとき, $\displaystyle\lim\limits_{n \to \infty}\int_0^xf_n(t)\,dt = 0$ である.
- (3)
- $-1 \leqq x \leqq 1$ のとき, \[\mathrm{arctan}\,x = \sum\limits_{n = 0}^\infty\frac{(-1)^n}{2n+1}x^{2n+1} \quad \cdots [*]\] である. 特に, $\dfrac{\pi}{4} = \displaystyle\sum\limits_{n = 0}^\infty\dfrac{(-1)^n}{2n+1}$ である.
解答例
- (1)
- 等比数列の和の公式により, \[ f_n(t) = \frac{1}{1+t^2}-\frac{1-(-t^2)^n}{1-(-t^2)} = \frac{(-t^2)^n}{1+t^2}\] である.
- (2)
- $x \geqq 0$ のとき, 積分の三角不等式により, \[\begin{aligned} \left|\int_0^xf_n(t)\,dt\right| &\leqq \int_0^x|f_n(t)|\,dt = \int_0^x\frac{t^{2n}}{1+t^2}\,dt \quad (\because (1)) \\ &\leqq \int_0^xt^{2n}\,dt = \left[\frac{t^{2n+1}}{2n+1}\right] _0^x = \frac{x^{2n+1}}{2n+1} \end{aligned}\] が成り立つ. $0 \leqq x \leqq 1$ のとき, 右辺は $0$ に収束するから, 挟みうちの原理により \[\lim_{n \to \infty}\int_0^xf_n(t)\,dt = 0\] である.
- (3)
- (i)
- $0 \leqq x \leqq 1$ のとき. $t = \tan\theta$ とおくと \[\frac{1}{1+t^2}\cdot\frac{dt}{d\theta} = \cos ^2\theta\cdot\frac{1}{\cos ^2\theta} = 1\] となるから, \[\begin{aligned} \int_0^xf_n(t)\,dt &= \int_0^x\frac{dt}{1+t^2}-\sum_{k = 0}^{n-1}\int_0^x(-t^2)^k\,dt \\ &= \int_0^{\mathrm{arctan}\,x}\,d\theta -\sum_{k = 0}^{n-1}(-1)^k\int_0^xt^{2k}\,dt \\ &= [\theta ]_0^{\mathrm{arctan}\,x}-\sum_{k = 0}^{n-1}(-1)^k\left[\frac{t^{2k+1}}{2k+1}\right] _0^x \\ &= \mathrm{arctan}\,x-\sum_{k = 0}^{n-1}\frac{(-1)^k}{2k+1}x^{2k+1} \end{aligned}\] が得られる. 両辺の極限をとると, (2) から \[ 0 = \mathrm{arctan}\,x-\sum_{n = 0}^\infty\frac{(-1)^n}{2n+1}x^{2n+1}\] となるので, $[*]$ が得られる.
- (ii)
- $-1 \leqq x < 0$ のとき. $-\tan\theta = \tan (-\theta )$ よって $\mathrm{arctan}\,(-x) = -\mathrm{arctan}\,x$ から, \[\begin{aligned} &\mathrm{arctan}\,x = \mathrm{arctan}\,(-|x|) = -\mathrm{arctan}\,|x| \\ &= -\sum\limits_{n = 0}^\infty\frac{(-1)^n}{2n+1}|x|^{2n+1} = \sum\limits_{n = 0}^\infty\frac{(-1)^n}{2n+1}(-|x|)^{2n+1} \\ &= \sum\limits_{n = 0}^\infty\frac{(-1)^n}{2n+1}x^{2n+1} \end{aligned}\] が成り立つ.
特に, $x = 1$ とすると $\dfrac{\pi}{4} = \displaystyle\sum\limits_{n = 0}^\infty\dfrac{(-1)^n}{2n+1}$ が得られる.
参考
- \[\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots = \frac{\pi}{4}\] と, 奇数の逆数に交互に符号をつけてすべて足し合わせると円周率が出てくることは, 非常に神秘的である. この無限級数は,「マーダヴァ=ライプニッツ級数」(Mādhava–Leibniz series) と呼ばれ, 収束が遅いため円周率の近似値の計算には実用的でないが, 円周率を表す無限級数としては世界で初めて発見されたものである (マーダヴァ, $15$ 世紀).
- (3) の等式 \[\arctan x = \sum\limits_{n = 0}^\infty\frac{(-1)^n}{2n+1}x^{2n+1} \quad (-1 \leqq x \leqq 1) \quad \cdots [\ast ]\] は $\mathrm{arctan}\,x$ の「マクローリン展開」(こちらを参照) であり, 右辺の無限級数は「グレゴリー=ライプニッツ級数」(Gregory–Leibniz series) と呼ばれる (特に $x = 1$ の場合が有名である). $[\ast ]$ と「マチンの公式」 \[\frac{\pi}{4} = 4\arctan\frac{1}{5}-\arctan\frac{1}{239}\] (こちらを参照) を組合せると, 比較的速く円周率に収束する無限級数が得られる.
問題《簡易版スターリングの公式》
次のことを示せ.
ただし, $\lim\limits_{x \to \infty}\dfrac{\log x}{x} = 0$ であることは, 証明なしに使ってよい.
- (1)
- $f(x) \geqq 0$ $(x \geqq 1)$ なる単調増加関数 $f(x)$ に対して, \[\int_1^n\!f(x)\,dx \!\leqq\! f(1)\!+\!\cdots\!+\!f(n) \leqq \int_1^n\!f(x)\,dx+f(n)\] が成り立つ.
- (2)
- $\lim\limits_{n \to \infty}\dfrac{\log n!-n\log n+n}{n} = 0$ が成り立つ.
解答例
- (1)
- $f(x)$ を $f(x) \geqq 0$ $(x \geqq 1)$ なる単調増加関数とすると,
$f(k) \leqq \displaystyle\int_k^{k+1}f(x)\,dx \leqq f(k+1)$ ($k$: 正の整数)となるから, $n > 1$ のとき, $1 \leqq k \leqq n-1$ なる $k$ について辺々を加えると \[ f(1)\!+\!\cdots\!+\!f(n-1) \!\leqq\! \int_1^n\!f(x)\,dx \!\leqq\! f(2)\!+\!\cdots\!+\!f(n)\] となり, \[\int_1^nf(x)\,dx \!\leqq\! f(1)\!+\!\cdots\!+\!f(n) \!\leqq\! \int_1^nf(x)\,dx\!+\!f(n)\] が得られる. これは $n = 1$ のときにも成り立つ.
- (2)
- $f(x) = \log x$ に (1) の結果を適用すると, \[\begin{aligned} \int_1^n\log x\,dx &= \big[ x\log x\big] _1^n-\int_1^nx\cdot\frac{1}{x}\,dx \\ &= n\log n-n+1 \end{aligned}\] であるので, \[ n\log n-n+1 \leqq \log n! \leqq n\log n-n+1+\log n\] から \[ 1 \leqq \log n!-n\log n+n \leqq 1+\log n\] が得られる. よって, \[\frac{1}{n} \leqq \frac{\log n!-n\log n+n}{n} \leqq \frac{1}{n}+\frac{\log n}{n}\] であり, $\lim\limits_{x \to \infty}\dfrac{\log x}{x} = 0$ であるから, \[\lim\limits_{n \to \infty}\frac{\log n!-n\log n+n}{n} = 0\] が成り立つ.
参考
本問で示した公式は「スターリングの公式」(Stirling's formula) と呼ばれる.
これを精密化した公式は, 二項分布は正規分布によって近似できるという「ド・モアブル=ラプラスの定理」(de Moivre-Laplace theorem) の証明に利用されるなど, 重要な応用をもつ.
問題《汎調和級数の収束域》
$s > 0$ とし, 各正の整数 $n$ に対して
\[ A_n = \sum_{k = 1}^n\frac{1}{k^s}, \quad I_n = \displaystyle\int_1^n\frac{dx}{x^s}\]
とおく.
- (1)
- 正の整数 $k$ に対して, $\displaystyle\frac{1}{(k+1)^s} \leqq \int_k^{k+1}\frac{dx}{x^s} \leqq \frac{1}{k^s}$ を示せ.
- (2)
- $A_n \leqq 1+I_n$ $(n > 1),$ $A_n \geqq I_{n+1}$ を示せ.
- (3)
- 極限 $\lim\limits_{n \to \infty}I_n$ を求めよ.
- (4)
- 無限級数 $A = \displaystyle\sum_{n = 1}^\infty\frac{1}{n^s}$ は, $s > 1$ のとき収束し, $0 < s \leqq 1$ のとき $\infty$ に発散することを示せ. ただし, ある定数 $M$ について $a_n \leqq M$ $(n \geqq 1)$ を満たす単調増加数列 $\{ a_n\}$ は収束するという定理は, 証明なしに使ってよい.
(参考: $1990$ 信州大)
解答例
- (1)
- $f(x) = \dfrac{1}{x^s}$ $(x > 0)$ とおく.
このとき, $s > 0$ から,
\[ f'(x) = -\frac{s}{x^{s+1}} < 0\]
が成り立つ.
よって, $f(x)$ は単調減少であるから, $k \leqq x \leqq k+1$ において
が成り立つ. $k$ から $k+1$ までの定積分をとると, 積分の単調性により \[\begin{aligned} \frac{1}{(k+1)^s} \leqq \int_k^{k+1}\frac{dx}{x^s} \leqq \frac{1}{k^s} \quad \cdots [1] \qquad& \\ \left(\because\int_k^{k+1}\,dx = [x]_k^{k+1} = 1\right)& \end{aligned}\] が得られる.
$f(k+1) \leqq f(x) \leqq f(k)$ つまり $\dfrac{1}{(k+1)^s} \leqq \dfrac{1}{x^s} \leqq \dfrac{1}{k^s}$ - (2)
- $n > 1$ のとき, $1 \leqq k \leqq n-1$ なる $k$ について $[1]$ の左側の辺々を加えると
となるから, 両辺に $1$ を加えると \[ A_n \leqq 1+I_n \quad \cdots [2]\] が得られる. また, $1 \leqq k \leqq n$ なる $k$ について $[1]$ の右側の辺々を加えると
$\displaystyle\sum_{k = 1}^{n-1}\frac{1}{(k+1)^s} \leqq \int_1^n\frac{dx}{x^s}$ つまり $\displaystyle\sum_{k = 2}^n\frac{1}{k^s} \leqq I_n$ が得られる.$\displaystyle\int_1^{n+1}\frac{dx}{x^s} \leqq \sum_{k = 1}^n\frac{1}{k^s}$ つまり $A_n \geqq I_{n+1} \quad \cdots [3]$ - (3)
- (i)
- $s = 1$ のとき. $n \to \infty$ とすると \[ I_n = \int_1^n\frac{dx}{x} = \big[\log x\big] _1^n = \log n \to \infty\] となる.
- (ii)
- $s \neq 1$ のとき. $n \to \infty$ とすると \[\begin{aligned} I_n &= \int_1^n\frac{dx}{x^s} = \left[\frac{-1}{(s-1)x^{s-1}}\right] _1^n = \frac{1}{s-1}\left( 1-\frac{1}{n^{s-1}}\right) \\ &\to \begin{cases} \infty & (0 < s < 1), \\ \dfrac{1}{s-1} & (s > 1) \end{cases} \end{aligned}\] となる.
- (4)
- $s > 1$ のとき. $[2]$ の右辺は $1+\dfrac{1}{s-1}$ に収束し, よって $A_n \leqq 1+\dfrac{1}{s-1}$ が成り立つ. また, $\{ A_n\}$ は単調増加であるから, 定理により, $A = \displaystyle\sum_{n = 1}^\infty\frac{1}{n^s}$ は収束する.
- $0 < s \leqq 1$ のとき. $[3]$ の右辺は $\infty$ に発散するから, 追い出しの原理により, $A = \displaystyle\lim\limits_{n \to \infty}A_n$ は $\infty$ に発散する.
参考
- $\displaystyle\sum_{n = 1}^\infty\frac{1}{n}$ を「調和級数」(harmonic series), $\displaystyle\sum_{n = 1}^\infty\frac{1}{n^s}$ を「汎調和級数」と呼ぶ ((4) の別解についてはこちらを参照). 「汎調和級数」は「リーマン・ゼータ関数」(Riemann zeta function) に一般化される.
- 一般に, 各項が一定値以下の値をとる単調増加数列 (または常に一定値以上の値をとる単調減少数列) は収束することが知られている.
よって, 各項が非負の無限級数,「正項級数」(positive series) については, 部分和が単調増加数列をなすことから, 収束するか $\infty$ に発散するかのいずれかが起こる.
ここで,「正項級数」の収束判定法についてまとめておく.
- (1)
- 「比較判定法」: 各項が正である無限級数 $A = \displaystyle\sum_{n = 1}^\infty a_n,$ $B = \displaystyle\sum_{n = 1}^\infty b_n$ に対して, $a_n \leqq b_n$ $(n \geqq 1)$ であるとき, $B$ が収束する $\Longrightarrow$ $A$ が収束する.
- (2)
- 「積分判定法」: $x \geqq 1$ において $f(x) \geqq 0$ を満たす連続な単調減少関数 $f(x)$ に対して, $\displaystyle\sum_{n = 1}^\infty f(n)$ が収束する $\iff$ $\displaystyle\lim\limits_{n \to \infty}\int_1^nf(x)\,dx$ が収束する.
問題《素数の逆数和の発散》
$n$ 番目に小さい素数を $p_n$ で表し, 正の整数 $n,$ 素数 $p$ に対して
\[ f(n,p) = \sum_{k = 0}^n\frac{1}{p^k}\]
と定める.
次のことを示せ.
- (1)
- \[\sum_{k = 1}^n\frac{1}{k} < f(n,p_1)\cdots f(n,p_n)\] が成り立つ.
- (2)
- \[\sum_{n = 1}^\infty\left\{ -\log\left( 1-\frac{1}{p_n}\right)\right\} = \infty\] である.
- (3)
- \[\sum_{n = 1}^\infty\frac{1}{p_n} = \infty\] である.
(参考: $2014$ 大阪大)
解答例
- (1)
- $n$ 以下の正の整数 $k$ は $n$ 番目までの素数 $p_1,$ $\cdots,$ $p_n$ を用いて
の形に表される. このとき, $k$ の逆数は \[\frac{1}{k} = \frac{1}{p_1{}^{e_1}\cdots p_n{}^{e_n}}\] と表され, これは \[ f(n,p_1)\cdots f(n,p_n) = \left(\sum_{k = 0}^n\frac{1}{p_1{}^k}\right)\cdots\left(\sum_{k = 0}^n\frac{1}{p_n{}^k}\right)\] の展開式の項 (すべて正) に含まれる. よって, \[\sum_{k = 1}^n\frac{1}{k} < f(n,p_1)\cdots f(n,p_n) \quad \cdots [1]\] が成り立つ.$k = p_1{}^{e_1}\cdots p_n{}^{e_n}$ ($e_1,$ $\cdots,$ $e_n$: $n$ 以下の非負整数) - (2)
- $[1]$ の右辺を変形すると \[\begin{aligned} \sum_{k = 1}^n\frac{1}{k} &< \frac{1-\left(\dfrac{1}{p_1}\right) ^{n+1}}{1-\dfrac{1}{p_1}}\cdot\cdots\cdot\frac{1-\left(\dfrac{1}{p_n}\right) ^{n+1}}{1-\dfrac{1}{p_n}} \\ &< \frac{1}{1-\dfrac{1}{p_1}}\cdot\cdots\cdot\frac{1}{1-\dfrac{1}{p_n}} \end{aligned}\] となるから, 両辺の自然対数をとると \[\log\sum_{k = 1}^n\frac{1}{k} < \sum_{k = 1}^n\left\{ -\log\left( 1-\frac{1}{p_k}\right)\right\} \quad \cdots [1]'\] が得られる. また, 関数 $y = \dfrac{1}{x}$ $(x > 0)$ は単調減少であるから \[\sum_{k = 1}^n\frac{1}{k} > \sum_{k = 1}^n\int_k^{k+1}\frac{dx}{x} = \int_1^{n+1}\frac{dx}{x} = [\log x]_1^{n+1} = \log (n+1)\] が成り立ち, 両辺の自然対数をとると \[\log\log (n+1) < \log\sum_{k = 1}^n\frac{1}{k}\] が得られる. $[1]',$ $[2]$ により \[\log\log (n+1) < \sum_{k = 1}^n\left\{ -\log\left( 1-\frac{1}{p_k}\right)\right\}\] が成り立ち, 左辺は $\infty$ に発散するから, \[\sum_{n = 1}^\infty\left\{ -\log\left( 1-\frac{1}{p_n}\right)\right\} = \infty \quad \cdots [3]\] である.
- (3)
- 不等式 \[ x > -\frac{1}{2}\log (1-x) \quad \left( 0 < x \leqq \frac{1}{2}\right) \quad \cdots [4]\] を示せば, \[\frac{1}{t} > -\frac{1}{2}\log\left( 1-\frac{1}{t}\right) \quad (t \geqq 2)\] が成り立つことから \[\sum_{n = 1}^\infty\frac{1}{p_n} > \frac{1}{2}\sum_{n = 1}^\infty\left\{ -\log\left( 1-\frac{1}{p_n}\right)\right\}\] であり, $[3]$ により \[\sum_{n = 1}^\infty\frac{1}{p_n} = \infty \quad \cdots [5]\] であることがわかる. そこで, $[4]$ を示す. \[ f(x) = 2x+\log (1-x) \quad (x < 1)\] の導関数は \[ f'(x) = 2+\frac{-1}{1-x} = \frac{1-2x}{1-x}\] であり, $0 < x \leqq \dfrac{1}{2}$ において $f'(x) \geqq 0$ であることから \[ f(x) \geqq f\left(\frac{1}{2}\right) = 1+\log\frac{1}{2} = \log e-\log 2 > 0\] よって $[4]$ が成り立つ. 以上により, $[5]$ が示された.
参考
- 素数の逆数和が $\infty$ に発散することは, オイラーにより証明された.
- 差が $2$ である素数の対を「双子素数」(twin prime) と呼ぶ. 「双子素数」の逆数和は収束することが知られており, その和を「ブルン定数」(Brun's constant) と呼ぶ. 「双子素数」が無限に存在するか否かは未解決である.
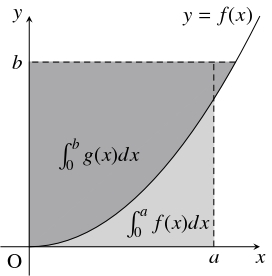
問題《定積分に関するヤングの不等式》
区間 $[0,c)$ で連続, $(0,c)$ で微分可能な単調増加関数 $f(x)$ が $f(0) = 0$ を満たすとして, $g(x)$ を $f(x)$ の逆関数とする.
また, $0 < a < c,$ $0 < b < f(c)$ とする.
- (1)
- $h(a) = ab-\displaystyle\int_0^af(x)\,dx$ は $a = g(b)$ において最大値をとることを示せ.
- (2)
- $\displaystyle\int_0^{g(b)}f(x)\,dx$ を変形することで, $h(g(b)) = \displaystyle\int_0^bg(x)\,dx$ を示せ.
- (3)
- $\displaystyle\int_0^af(x)\,dx+\int_0^bg(x)\,dx \geqq ab$ を示せ.
- (4)
- $p,$ $q$ を $\dfrac{1}{p}+\dfrac{1}{q} = 1$ なる正の数とする. 関数 $f(x) = x^{p-1}$ に (3) の結果を適用することにより, $\dfrac{a^p}{p}+\dfrac{b^q}{q} \geqq ab$ を示せ.
(参考: $2020$ 大阪市立大)
解答例
- (1)
- \[ h'(a) = b-f(a) = f(g(b))-f(a)\] であり, $f(x)$ は単調増加であるから, \[\begin{aligned} h'(a) \geqq 0 &\iff a \leqq g(b), \\ h'(a) \leqq 0 &\iff a \geqq g(b) \end{aligned}\] である. よって, $h(a)$ は $a = g(b)$ において極大かつ最大の値 \[ h(g(b)) = bg(b)-\int_0^{g(b)}f(x)\,dx \quad \cdots [1]\] をとる.
- (2)
- $f(x) = x'f(x)$ であり, $y = f(x)$ とおくと $x = g(y)$ となるから, \[\begin{aligned} \int_0^{g(b)}f(x)\,dx &= \int_0^{g(b)}x'f(x)\,dx \\ &= [xf(x)]_0^{g(b)}-\int_0^{g(b)}xf'(x)\,dx \\ &= g(b)f(g(b))-\int_0^bg(y)\,dy \\ &= bg(b)-\int_0^bg(x)\,dx \quad \cdots [2] \end{aligned}\] である. よって, $[1],$ $[2]$ から \[ h(g(b)) = \int_0^bg(x)\,dx \quad \cdots [3]\] が得られる.
- (3)
- (1) で示したことから $h(a) \leqq h(g(b))$ であるので, $[3]$ から \[\begin{aligned} &ab-\int_0^af(x)\,dx \leqq \int_0^bg(x)\,dx \\ &\int_0^af(x)\,dx+\int_0^bg(x)\,dx \geqq ab \end{aligned}\] が得られる.
- (4)
- $\dfrac{1}{p}+\dfrac{1}{q} = 1$ から, \[ p-1 = \frac{1}{1-\dfrac{1}{q}}-1 = \frac{q}{q-1}-1 = \frac{1}{q-1}\] が成り立つ. よって, $y = x^{p-1}$ とおくと, $x = y^{\frac{1}{p-1}} = y^{q-1}$ となるから, $f(x) = x^{p-1}$ の逆関数は $g(x) = x^{q-1}$ である. よって, (3) の結果により, \[\begin{aligned} ab &\leqq \int_0^ax^{p-1}\,dx+\int_0^bx^{q-1}\,dx \\ &= \left[\frac{x^p}{p}\right] _0^a+\left[\frac{x^q}{q}\right] _0^b \\ &= \frac{a^p}{p}+\frac{b^q}{q} \end{aligned}\] が得られる.
参考
(3) は, (4) の「ヤングの不等式」(Young's inequality, 別証明はこちらを参照) の一般化であり, 定積分に関する「ヤングの不等式」として知られている.
この不等式が成り立つことは, 直感的には, 次の図からわかる.