曲線の長さ
曲線の長さ (媒介変数表示)
定義《平面曲線》
ある実数値連続関数 $f(t),$ $g(t)$ $(a \leqq t \leqq b)$に対して
\[ x = f(t), \quad y = g(t) \quad (a \leqq t \leqq b)\]
で定義される点 $(x,y)$ 全体のなす集合を平面曲線 (plane curve) または単に曲線と呼ぶ.
定義《平面曲線の長さ》
平面曲線 $C:x = f(t),$ $y = g(t)$ $(a \leqq t \leqq b)$ に対して, $C$ 上の任意個の点
\[\mathrm P_k(f(t_k),g(t_k)), \quad a = t_0 < t_1 < \cdots < t_n = b\]
を順に結ぶ折れ線の長さ
\[\sum_{k = 1}^n\mathrm P_{k-1}\mathrm P_k\]
の「上限」(どの折れ線の長さよりも大きい実数の最小値) が存在するとき, その値を $C$ の長さ (length) と呼ぶ.
定理《平面曲線の長さ》
- (1)
- 閉区間 $[a,b]$ で連続で開区間 $(a,b)$ で微分可能な実数値関数 $f(t),$ $g(t)$ の導関数が連続であるとき, 平面曲線 $x = f(t),$ $y = g(t)$ $(a \leqq t \leqq b)$ の長さ $L$ は \[ L = \int _a^b\sqrt{f'(t)^2+g'(t)^2}\,dt\] である.
- (2)
- 閉区間 $[a,b]$ で連続で開区間 $(a,b)$ で微分可能な実数値関数 $f(x)$ の導関数が連続であるとき, $f(x)$ のグラフ $y = f(x)$ $(a \leqq x \leqq b)$ の長さ $L$ は \[ L = \int _a^b\sqrt{1+f'(x)^2}\,dx\] である.
- (3)
- 閉区間 $[a,b]$ で連続で開区間 $(a,b)$ で微分可能な実数値関数 $r(\theta )$ の導関数が連続であるとき, 極方程式 $r = r(\theta )$ $(a \leqq \theta \leqq b)$ で表された曲線の長さ $L$ は \[ L = \int _a^b\sqrt{r'(\theta )^2+r(\theta )^2}\,d\theta\] である.
証明
- (2)
- (1) において $f(t),$ $g(t)$ をそれぞれ $t,$ $f(t)$ に置き換えると, 求める等式が得られる.
- (3)
- $x = r(\theta )\cos\theta,$ $y = r(\theta )\sin\theta$ とおく. このとき, \[\begin{aligned} \frac{dx}{d\theta} &= r'(\theta )\cos\theta -r(\theta )\sin\theta, \\ \quad \frac{dy}{d\theta} &= r'(\theta )\sin\theta +r(\theta )\cos\theta \end{aligned}\] となり, \[\begin{aligned} &\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2 \\ &= \{ r'(\theta )\cos\theta -r(\theta )\sin\theta\} ^2+\{ r'(\theta )\sin\theta +r(\theta )\cos\theta\} ^2 \\ &= r'(\theta )^2(\cos ^2\theta +\sin ^2\theta )+r(\theta )^2(\cos ^2\theta +\sin ^2\theta ) \\ &= r'(\theta )^2+r(\theta )^2 \end{aligned}\] となるから, \[ L = \int _a^b\sqrt{r'(\theta )^2+r(\theta )^2}\,d\theta\] が成り立つ.
問題《サイクロイドの長さ》
サイクロイド
\[ x = \theta -\sin\theta, \quad y = 1-\cos\theta \quad (0 \leqq \theta \leqq 2\pi )\]
の長さ $L$ を求めよ.
解答例
$x = \theta -\sin\theta,$ $y = 1-\cos\theta$ を $\theta$ で微分すると
\[\frac{dx}{d\theta} = 1-\cos\theta, \quad \frac{dy}{d\theta} = \sin\theta\]
となるから
\[\begin{aligned}
\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2 &= (1-\cos\theta )^2+\sin ^2\theta \\
&= 1-2\cos\theta +\cos ^2\theta +\sin ^2\theta \\
&= 2-2\cos\theta = 4\sin ^2\frac{\theta}{2} \\
\end{aligned}\]
であり, $0 \leqq \theta \leqq 2\pi$ において $\sin\dfrac{\theta}{2} \geqq 0$ である.
ゆえに, 求める長さは,
\[\begin{aligned}
L &= \int_0^{2\pi}\sqrt{\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2 }\,d\theta \\
&= \int_0^{2\pi}\sqrt{4\sin ^2\frac{\theta}{2}}\,d\theta \\
&= 2\int_0^{2\pi}\sin\frac{\theta}{2}\,d\theta \\
&= 2\left[ -2\cos\frac{\theta}{2}\right] _0^{2\pi} \\
&= 2\cdot (-2)(-1-1) = 8
\end{aligned}\]
である.
問題《カージオイドの長さ》
カージオイド
\[ x = (1+\cos\theta )\cos\theta, \quad y = (1+\cos\theta )\sin\theta \quad (-\pi \leqq \theta \leqq \pi )\]
の長さ $L$ を求めよ.
解答例
$x = (1+\cos\theta )\cos\theta,$ $y = (1+\cos\theta )\sin\theta$ を $\theta$ で微分すると
\[\begin{aligned}
\frac{dx}{d\theta} &= (-\sin\theta )\cos\theta +(1+\cos\theta )(-\sin\theta ) \\
&= -2\sin\theta\cos\theta -\sin\theta \\
&= -\sin 2\theta -\sin\theta, \\
\frac{dy}{d\theta} &= (-\sin\theta )\sin\theta +(1+\cos\theta )\cos\theta \\
&= (\cos ^2\theta -\sin ^2\theta )+\cos\theta \\
&= \cos 2\theta +\cos\theta
\end{aligned}\]
となるから
\[\begin{aligned}
\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2 &= (-\sin 2\theta -\sin\theta )^2+(\cos 2\theta +\cos\theta )^2 \\
&= \sin ^22\theta +2\sin 2\theta\sin\theta +\sin ^2\theta \\
&\qquad +\cos ^22\theta +2\cos 2\theta\cos\theta +\cos ^2\theta \\
&= 2+2\cos (2\theta -\theta ) \\
&= 2(1+\cos\theta ) \\
&= 4\cos ^2\frac{\theta}{2}
\end{aligned}\]
であり, $-\pi \leqq \theta \leqq \pi$ において $\cos\dfrac{\theta}{2} \geqq 0$ である.
ゆえに, 求める長さは,
\[\begin{aligned}
L &= \int_0^{2\pi}\sqrt{\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2}\,d\theta \\
&= \int_{-\pi}^\pi\sqrt{4\cos ^2\frac{\theta}{2}}\,d\theta \\
&= 2\int_{-\pi}^\pi\cos\frac{\theta}{2}\,d\theta \\
&= 4\int_0^\pi\cos\frac{\theta}{2}\,d\theta \\
&= 4\left[ 2\sin\frac{\theta}{2}\right] _0^\pi \\
&= 4\cdot 2(1-0) = 8
\end{aligned}\]
である.
別解
この曲線は極方程式
\[ r = 1+\cos\theta \quad (-\pi \leqq \theta \leqq \pi )\]
で表されるから, 求める長さは,
\[\begin{aligned}
L &= \int_{-\pi}^\pi\sqrt{r^2+\left(\frac{dr}{d\theta}\right) ^2}\,d\theta \\
&= \int_{-\pi}^\pi\sqrt{(1+\cos\theta )^2+(-\sin\theta )^2}\,d\theta \\
&= \int_{-\pi}^\pi\sqrt{1+2\cos\theta +\cos ^2\theta +\sin ^2\theta}\,d\theta \\
&= \int_{-\pi}^\pi\sqrt{2(1+\cos\theta )}\,d\theta \\
&= \int_{-\pi}^\pi\sqrt{4\cos ^2\frac{\theta}{2}}\,d\theta \\
&= 2\int_{-\pi}^\pi\cos\frac{\theta}{2}\,d\theta \\
&= 4\int_0^\pi\cos\frac{\theta}{2}\,d\theta \\
&= 4\left[ 2\sin\frac{\theta}{2}\right] _0^\pi \\
&= 4\cdot 2(1-0) = 8
\end{aligned}\]
である.
問題《アストロイドの長さ》
アストロイド
\[ x = \cos ^3\theta, \quad y = \sin ^3\theta \quad (0 \leqq \theta \leqq 2\pi )\]
の長さ $L$ を求めよ.
解答例
\[\cos ^3(2\pi -\theta ) = \cos ^3\theta, \quad \sin ^3(2\pi -\theta ) = -\sin ^3\theta\]
から曲線は $x$ 軸に関して対称,
\[\cos ^3(\pi -\theta ) = -\cos ^3\theta, \quad \sin ^3(\pi -\theta ) = \sin ^3\theta\]
から曲線は $y$ 軸に関して対称である.
よって,
\[ L = 4\int_0^{\frac{\pi}{2}}\sqrt{\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2}\,d\theta\]
である.
$x = \cos ^3\theta,$ $y = \sin ^3\theta$ を $\theta$ で微分すると
\[\frac{dx}{d\theta} = -3\cos ^2\theta\sin\theta, \quad \frac{dy}{d\theta} = 3\sin ^2\theta\cos\theta\]
となるから
\[\begin{aligned}
\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2 &= (-3\cos ^2\theta\sin\theta )^2+(3\sin ^2\theta\cos\theta )^2 \\
&= 9\cos ^4\theta\sin ^2\theta +9\sin ^4\theta\cos ^2\theta \\
&= 9\sin ^2\theta\cos ^2\theta (\cos ^2\theta +\sin ^2\theta ) \\
&= \frac{9}{4}(2\sin\theta\cos\theta )^2 \\
&= \frac{9}{4}\sin ^22\theta
\end{aligned}\]
であり, $0 \leqq \theta \leqq \dfrac{\pi}{2}$ において $\sin 2\theta \geqq 0$ である.
ゆえに, 求める長さは,
\[\begin{aligned}
L &= 4\int_0^{\frac{\pi}{2}}\sqrt{\frac{9}{4}\sin ^22\theta}\,d\theta \\
&= 4\cdot\frac{3}{2}\int_0^{\frac{\pi}{2}}\sin 2\theta\,d\theta \\
&= 6\left[ -\frac{\cos 2\theta}{2}\right] _0^{\frac{\pi}{2}} \\
&= -3(-1-1) = 6
\end{aligned}\]
である.
問題《円の伸開線の長さ》
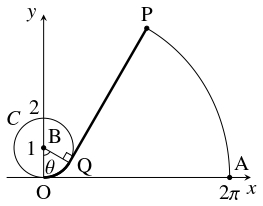
一端が原点 $\mathrm O(0,\ 0)$ に固定された伸び縮みのしない長さ $2\pi$ の細いひもがある.
他端 $\mathrm P$ が点 $\mathrm A(2\pi,0)$ 上にある状態から,
ひもを円周 $C:x^2+(y-1)^2 = 1$ 上に反時計回りにたるみなく巻きつける.
- (1)
- 円周 $C$ の中心を $\mathrm B$ とおき, $C$ 上の点 $\mathrm Q$ までひもを巻きつけたとき, $\theta = \angle\mathrm{OBQ}$ とおく. $\theta$ を用いて $\overrightarrow{\mathrm{OP}}$ を表せ.
- (2)
- 点 $\mathrm P$ が描く曲線の長さ $L$ を求めよ.
解答例
- (1)
- $\angle\mathrm{OBQ} = \theta$ のとき $\mathrm Q(\sin\theta,1-\cos\theta )$ であるから,
\[\begin{aligned}
\overrightarrow{\mathrm{BQ}} &= \overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OB}} \\
&= (\sin\theta,1-\cos\theta )-(0,1) \\
&= (\sin\theta,-\cos\theta )
\end{aligned}\]
で, この単位法線ベクトルは
\[\pm (\cos\theta,\sin\theta )\]
である.
$\overrightarrow{\mathrm{QP}}$ は $\vec n = (\cos\theta,\sin\theta )$ を $\mathrm{PQ} = \mathrm{OA}-\stackrel{\frown}{\mathrm{OQ}} = 2\pi -\theta$ 倍に伸ばしたベクトルであるから,
\[\begin{aligned}
&\overrightarrow{\mathrm{OP}} = \overrightarrow{\mathrm{OQ}}+\overrightarrow{\mathrm{QP}} \\
&= \overrightarrow{\mathrm{OQ}}+(2\pi -\theta )\vec n \\
&= (\sin\theta,1-\cos\theta )+(2\pi -\theta )(\cos\theta,\sin\theta ) \\
&= (\sin\theta +(2\pi -\theta )\cos\theta,1-\cos\theta +(2\pi -\theta )\sin\theta )
\end{aligned}\]
である.
- (2)
- \[\begin{aligned} x &= \sin\theta +(2\pi -\theta )\cos\theta, \\ y &= 1-\cos\theta +(2\pi -\theta )\sin\theta \end{aligned}\] とおくと, \[\begin{aligned} \frac{dx}{d\theta} &= \cos\theta -\cos\theta +(2\pi -\theta )(-\sin\theta ) \\ &= -(2\pi -\theta )\sin\theta, \\ \frac{dy}{d\theta} &= \sin\theta -\sin\theta +(2\pi -\theta )\cos\theta \\ &= (2\pi -\theta )\cos\theta \end{aligned}\] となる. よって, 求める曲線の長さは, \[\begin{aligned} L &= \int _0^{2\pi}\sqrt{\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2}\,d\theta \\ &= \int _0^{2\pi}(2\pi -\theta )\,d\theta \\ &= \left[ 2\pi\theta -\frac{\theta ^2}{2}\right] _0^{2\pi} \\ &= 2\pi ^2 \end{aligned}\] である.
参考
伸び縮みのしないひもをある図形にたるみなく巻きつけていくとき, またはそれをたるみなくほどいていくとき, ひもの先端が描く軌跡はその図形の「伸開線」または「インボリュート」(involute) と呼ばれる.
問題《らせんの長さ》
- (A)
- (1)
- 実数全体を定義域とする関数 $f(x) = \log (x+\sqrt{1+x^2})$ について, 導関数 $f'(x)$ を求めよ.
- (2)
- 極方程式 $r = \theta$ で定義される曲線の, $0 \leqq \theta \leqq 2\pi$ の部分の長さ $L$ を求めよ.
(参考: $2002$ 京都大)- (B)
- 極方程式 $r = e^\theta$ で定義される曲線の, $0 \leqq \theta \leqq 2\pi$ の部分の長さ $L$ を求めよ.
解答例
- (A)
- (1)
- $\{ \log u(x)\}' = \dfrac{u'(x)}{u(x)}$ から, \[ f'(x) = \frac{1+\dfrac{2x}{2\sqrt{1+x^2}}}{x+\sqrt{1+x^2}} = \frac{\dfrac{\sqrt{1+x^2}+x}{\sqrt{1+x^2}}}{x+\sqrt{1+x^2}} = \frac{1}{\sqrt{1+x^2}}\] である.
- (2)
- 曲線 $r = \theta$ $(0 \leqq \theta \leqq 2\pi )$ について, $x = r\cos\theta,$ $y = r\sin\theta$ とおく. このとき, \[\begin{aligned} &\frac{dx}{d\theta} = \cos\theta -\theta\sin\theta, \\ &\frac{dy}{d\theta} = \sin\theta +\theta\cos\theta, \\ &\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2 = 1+\theta ^2 \end{aligned}\] から \[\begin{aligned} L &= \int_0^{2\pi}\sqrt{1+\theta ^2}\,d\theta \\ &= [\theta\sqrt{1+\theta ^2}]_0^{2\pi}-\int_0^{2\pi}\frac{\theta ^2}{\sqrt{1+\theta ^2}}\,d\theta \\ &= 2\pi\sqrt{1+4\pi ^2}-\int_0^{2\pi}\frac{1+\theta ^2-1}{\sqrt{1+\theta ^2}}\,d\theta \\ &= 2\pi\sqrt{1+4\pi ^2}-L+\int_0^{2\pi}\frac{d\theta}{\sqrt{1+\theta ^2}}, \\ 2L &= 2\pi\sqrt{1+4\pi ^2}+[\log (\theta +\sqrt{1+\theta ^2})]_0^{2\pi} \\ &= 2\pi\sqrt{1+4\pi ^2}+\log (2\pi +\sqrt{1+4\pi ^2}) \end{aligned}\] であるので, 求める長さは \[ L = \pi\sqrt{1+4\pi ^2}+\frac{1}{2}\log (2\pi +\sqrt{1+4\pi ^2})\] である.
- (B)
- 曲線 $r = e^\theta$ $(0 \leqq \theta \leqq 2\pi )$ について, $x = r\cos\theta,$ $y = r\sin\theta$ とおく. このとき, \[\begin{aligned} &\frac{dx}{d\theta} = e^\theta (\cos\theta -\sin\theta ), \\ &\frac{dy}{d\theta} = e^\theta (\sin\theta +\cos\theta ), \\ &\left(\frac{dx}{d\theta}\right) ^2+\left(\frac{dy}{d\theta}\right) ^2 \\ &= e^{2\theta}(\cos\theta -\sin\theta )^2+e^{2\theta}(\sin\theta +\cos\theta )^2 \\ &= 2e^{2\theta} \end{aligned}\] となるので, 求める長さは \[ L = \int_0^{2\pi}\sqrt 2e^\theta\,d\theta = \sqrt 2[e^\theta ]_0^{2\pi} = \sqrt 2(e^{2\pi}-1)\] である.
別解
- (A)
- (2)
- 求める曲線の長さは \[ L = \int_0^{2\pi}\sqrt{\left(\frac{dr}{d\theta}\right) ^2+r^2}\,d\theta = \int_0^{2\pi}\sqrt{1+\theta ^2}\,d\theta\] で, 以下同様である.
- (B)
- 求める曲線の長さは, \[\begin{aligned} L &= \int_0^{2\pi}\sqrt{\left(\frac{dr}{d\theta}\right) ^2+r^2}\,d\theta = \int_0^{2\pi}\sqrt{e^{2\theta}+e^{2\theta}}\,d\theta \\ &= \sqrt 2\int_0^{2\pi}e^\theta\,d\theta = \sqrt 2[e^\theta ]_0^{2\pi} = \sqrt 2(e^{2\pi}-1) \end{aligned}\] である.
曲線の長さ (関数のグラフ)
問題《懸垂線の長さ》
$f(x) = \dfrac{e^x+e^{-x}}{2}$ とおき, 曲線 $y = f(x)$ の点 $\mathrm P(t,f(t))$ $(t \geqq 0)$ における接線に点 $\mathrm H(t,0)$ から下ろした垂線の足を $\mathrm Q$ とおく.
次のことを示せ.
- (1)
- 曲線 $y = f(x)$ の点 $\mathrm A(0,f(0))$ から $\mathrm P$ までの弧長 $\overset{\frown}{\mathrm{AP}}$ は $f'(t)$ に等しい.
- (2)
- $\overset{\frown}{\mathrm{AP}} = \mathrm{PQ}$ が成り立つ.
(参考: 室蘭工業大)
解答例
- (1)
- $f'(x) = \dfrac{e^x-e^{-x}}{2},$ $f''(x) = \dfrac{e^x+e^{-x}}{2} = f(x) \geqq 0$ から \[\begin{aligned} 1+f'(x)^2 &= 1\!+\!\left(\frac{e^x\!-\!e^{-x}}{2}\right) ^2 \!= 1\!+\!\frac{e^{2x}\!-\!2\!+\!e^{-2x}}{4} \\ &= \frac{e^{2x}+2+e^{-2x}}{4} = \left(\frac{e^x+e^{-x}}{2}\right) ^2 \\ &= f(x)^2 = f''(x)^2 \end{aligned}\] であるので, \[\begin{aligned} \overset{\frown}{\mathrm{AP}} &= \int_0^t\sqrt{1+f'(x)^2}\,dx = \int_0^tf''(x)\,dx \\ &= \left[ f'(x)\right] _0^t = f'(t) \end{aligned}\] が成り立つ.
- (2)
- 直線 $\mathrm{QH}$ は点 $(t,0)$ を通り, 接線 $\mathrm{PQ}$ に垂直であるから, その方程式は
である. よって, 点 $\mathrm P(t,f(t))$ と直線 $\mathrm{QH}$ の距離について \[\begin{aligned} \mathrm{PQ} &= \frac{|t+f'(t)f(t)-t|}{\sqrt{1+f'(t)^2}} = \frac{f'(t)f(t)}{f(t)} \\ &= f'(t) = \overset{\frown}{\mathrm{AP}} \quad (\because (1)) \end{aligned}\] が成り立つ.
$y = -\dfrac{1}{f'(t)}(x-t)$ つまり $x+f'(t)y-t = 0$ 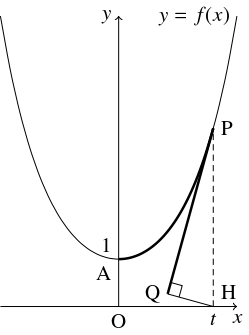
参考
両端を固定して鎖を垂らしたときにできる曲線は, 「懸垂線」または「カテナリー」(catenary) と呼ばれ, $y = a\cosh\dfrac{x}{a}$ $(a > 0)$ で表される.
ここで, $\cosh x = \dfrac{e^x+e^{-x}}{2}$ は「双曲線関数」(hypabolic function) である.
その名の通り, $\sinh x = \dfrac{e^x-e^{-x}}{2}$ との間には, $(\cosh x)^2-(\sinh x)^2 = 1$ という関係がある.
問題《放物線の長さ》
- (1)
- 不定積分 $\displaystyle\int\frac{dx}{\sqrt{x^2+a^2}}$ を求めよ.
(ヒント: $t = x+\sqrt{x^2+a^2}$ と置換する.) - (2)
- 不定積分 $\displaystyle\int\sqrt{x^2+a^2}\,dx$ を求めよ.
(ヒント: $\sqrt{x^2+a^2} = (x)'\sqrt{x^2+a^2}$ と考える.) - (3)
- 放物線 $y = x^2$ $(0 \leqq x \leqq 1)$ の長さ $L$ を求めよ.
解答例
- (1)
- $t = x+\sqrt{x^2+a^2}$ とおくと, \[\frac{dt}{dx} = 1+\frac{2x}{2\sqrt{x^2+a^2}} = \frac{t}{\sqrt{x^2+a^2}}\] よって \[\frac{1}{\sqrt{x^2+a^2}}\cdot\frac{dx}{dt} = \frac{1}{t}\] となるから, 求める不定積分は \[\begin{aligned} &\int\frac{dx}{\sqrt{x^2+a^2}} = \int\frac{dt}{t} \\ &= \log t+C = \log (x+\sqrt{x^2+a^2})+C \end{aligned}\] ($C$: 積分定数) である.
- (2)
- \[\begin{aligned} &\int\sqrt{x^2+a^2}\,dx = \int (x)'\sqrt{x^2+a^2}\,dx \\ &= x\sqrt{x^2+a^2}-\int x\cdot\frac{2x}{2\sqrt{x^2+a^2}}\,dx \\ &= x\sqrt{x^2+a^2}-\int\frac{(x^2+a^2)-a^2}{\sqrt{x^2+a^2}}\,dx \\ &= x\sqrt{x^2+a^2}-\int\sqrt{x^2+a^2}\,dx+a^2\int\frac{dx}{\sqrt{x^2+a^2}} \end{aligned}\] と (1) の結果により, \[\begin{aligned} &\int\sqrt{x^2+a^2}\,dx \\ &= \frac{1}{2}\left( x\sqrt{x^2+a^2}+a^2\int\frac{dx}{\sqrt{x^2+a^2}}\right) \\ &= \frac{1}{2}\left\{ x\sqrt{x^2+a^2}+a^2\log (x+\sqrt{x^2+a^2})\right\} +C \end{aligned}\] ($C$: 積分定数) である.
- (3)
- (2) の結果から, \[\begin{aligned} L &= \int_0^1\sqrt{1+\left(\frac{dy}{dx}\right) ^2}\,dx \\ &= \int_0^1\sqrt{1+(2x)^2}\,dx = 2\int_0^1\sqrt{x^2+\frac{1}{4}}\,dx \\ &= 2\cdot\frac{1}{2}\left[ x\sqrt{x^2+\frac{1}{4}}+\frac{1}{4}\log\left( x+\sqrt{x^2+\frac{1}{4}}\right)\right] _0^1 \\ &= \frac{\sqrt 5}{2}+\frac{1}{4}\log\left( 1+\frac{\sqrt 5}{2}\right) -\frac{1}{4}\log\frac{1}{2} \\ &= \frac{\sqrt 5}{2}+\frac{1}{4}\log\frac{1+\dfrac{\sqrt 5}{2}}{\dfrac{1}{2}} = \frac{\sqrt 5}{2}+\frac{1}{4}\log (2+\sqrt 5) \end{aligned}\] である.
別解 0
- (2)
- $t = x+\sqrt{x^2+a^2}$ とおく. このとき, $t-x = \sqrt{x^2+a^2}$ から $(t-x)^2 = x^2+a^2,$ $t^2-2xt = a^2,$ よって \[ x = \frac{1}{2}\left( t-\frac{a^2}{t}\right)\] となる. また, \[\frac{dx}{dt} = \frac{1}{2}\left( 1+\frac{a^2}{t^2}\right)\] であり, \[\begin{aligned} x^2+a^2 &= \frac{1}{4}\left( t-\dfrac{a^2}{t}\right) ^2+a^2 \\ &= \frac{1}{4}\left( t^2-2a^2+\frac{a^4}{t^2}+4a^2\right) \\ &= \frac{1}{4}\left( t^2+2a^2+\frac{a^4}{t^2}\right) = \frac{1}{4}\left( t+\frac{a^2}{t}\right) ^2, \\ t+\frac{a^2}{t} &= 2\sqrt{x^2+a^2}, \\ t-\frac{a^2}{t} &= 2x \end{aligned}\] であるから, 求める不定積分は \[\begin{aligned} &\int\sqrt{x^2+a^2}\,dx \\ &= \int\sqrt{\frac{1}{4}\left( t+\frac{a^2}{t}\right) ^2}\cdot\frac{1}{2}\left( 1+\frac{a^2}{t^2}\right)\,dt \\ &= \int\frac{1}{2}\left( t+\frac{a^2}{t}\right)\cdot\frac{1}{2}\left( 1+\frac{a^2}{t^2}\right)\,dt \\ &= \frac{1}{4}\int\left( t+\frac{2a^2}{t}+\frac{a^4}{t^3}\right)\,dt \\ &= \frac{1}{4}\left(\frac{t^2}{2}+2a^2\log t-\frac{a^4}{2t^2}\right) +C \\ &= \frac{1}{8}\left( t^2-\frac{a^4}{t^2}\right) +\frac{a^2}{2}\log t+C \\ &= \frac{1}{8}\left( t+\frac{a^2}{t}\right)\left( t-\frac{a^2}{t}\right) +\frac{a^2}{2}\log t+C \\ &= \frac{1}{8}\cdot 2\sqrt{x^2+a^2}\cdot 2x+\frac{a^2}{2}\log (x+\sqrt{x^2+a^2})+C \\ &= \frac{1}{2}\left\{ x\sqrt{x^2+a^2}+a^2\log (x+\sqrt{x^2+a^2})\right\} +C \end{aligned}\] ($C$: 積分定数) である.
別解 1
- (1)
- $x = \dfrac{1}{2}\left( t-\dfrac{a^2}{t}\right)$ $(t > 0)$ とおく. このとき, \[\frac{dx}{dt} = \frac{1}{2}\left( 1+\frac{a^2}{t^2}\right)\] であり, \[\begin{aligned} &x^2+a^2 = \frac{1}{4}\left( t-\dfrac{a^2}{t}\right) ^2+a^2 \\ &= \frac{1}{4}\left( t^2-2a^2+\frac{a^4}{t^2}+4a^2\right) = \frac{1}{4}\left( t^2+2a^2+\frac{a^4}{t^2}\right) \\ &= \frac{1}{4}\left( t+\frac{a^2}{t}\right) ^2 = \frac{t^2}{4}\left( 1+\frac{a^2}{t^2}\right) ^2 \end{aligned}\] である. また, $2xt = t^2-a^2$ つまり $t^2-2xt-a^2 = 0$ から \[ t = x+\sqrt{x^2+a^2}\] であるので, 求める不定積分は \[\begin{aligned} \int\frac{dx}{\sqrt{x^2+a^2}} &= \int\frac{\dfrac{1}{2}\left( 1+\dfrac{a^2}{t^2}\right)}{\sqrt{\dfrac{t^2}{4}\left( 1+\dfrac{a^2}{t^2}\right) ^2}}\,dt \\ &= \int\frac{dt}{t} = \log t+C \\ &= \log (x+\sqrt{x^2+a^2})+C \end{aligned}\] ($C$: 積分定数) である.
別解 2
- (1)
- $u = \log (x+\sqrt{x^2+a^2})$ とおくと \[\begin{aligned} \frac{du}{dx} &= \frac{1+\dfrac{2x}{2\sqrt{x^2+a^2}}}{x+\sqrt{x^2+a^2}} = \frac{\sqrt{x^2+a^2}+x}{(x+\sqrt{x^2+a^2})\sqrt{x^2+a^2}} \\ &= \frac{1}{\sqrt{x^2+a^2}} \end{aligned}\] から \[\frac{1}{\sqrt{x^2+a^2}}\cdot\frac{dx}{du} = 1\] となるので, 求める不定積分は \[\begin{aligned} \int\frac{dx}{\sqrt{x^2+a^2}} &= \int du = u+C \\ &= \log (x+\sqrt{x^2+a^2})+C \end{aligned}\] ($C$: 積分定数) である.
別解 3
- (1)
- $x = \dfrac{e^u-a^2e^{-u}}{2}$ とおく. このとき, \[\frac{dx}{du} = \frac{e^u+a^2e^{-u}}{2}\] であり, \[\begin{aligned} &x^2+a^2 = \left(\frac{e^u-a^2e^{-u}}{2}\right) ^2+a^2 \\ &= \frac{e^{2u}-2a^2+a^4e^{-2u}+4a^2}{4} \\ &= \frac{e^{2u}+2a^2+a^4e^{-2u}}{4} = \frac{(e^u+a^2e^{-u})^2}{4} \end{aligned}\] である. また, $2xe^u = e^{2u}-a^2$ つまり $e^{2u}-2xe^u-a^2 = 0$ から \[ e^u = x+\sqrt{x^2+a^2}, \quad u = \log (x+\sqrt{x^2+a^2})\] であるので, 求める不定積分は \[\begin{aligned} \int\frac{dx}{\sqrt{x^2+a^2}} &= \int\frac{\dfrac{e^u+a^2e^{-u}}{2}}{\sqrt{\dfrac{(e^u+a^2e^{-u})^2}{4}}}\,du \\ &= \int du = u+C \\ &= \log (x+\sqrt{x^2+a^2})+C \end{aligned}\] ($C$: 積分定数) である.
参考
- (1), (2) と同様に, \[\begin{aligned} &\int\frac{dx}{\sqrt{x^2-a^2}} = \log |x+\sqrt{x^2-a^2}|+C, \\ &\int\sqrt{x^2-a^2}\,dx \\ &= \frac{1}{2}\left\{ x\sqrt{x^2-a^2}-a^2\log |x+\sqrt{x^2-a^2}|\right\} +C \end{aligned}\] が成り立つ.
- 放物線の弧長のように, 楕円や双曲線の弧長を「初等関数」(多項式関数を係数とする方程式の解, 指数関数, 対数関数, 三角関数, 逆三角関数と, それらの合成関数) で求めることはできない. $0 < c < 1$ のとき, 楕円 $y = c\sqrt{1-x^2}$ $(0 \leqq x \leqq t)$ の長さは, $k = \sqrt{1-c^2}$ とおくと \[\begin{aligned} &\int_0^t\sqrt{1+\left(\frac{dy}{dx}\right) ^2}\,dx = \int_0^t\sqrt{1+\left(\frac{-2cx}{2\sqrt{1-x^2}}\right) ^2}\,dx \\ &= \int_0^t\sqrt{\frac{1-x^2+c^2x^2}{1-x^2}}\,dx = \int_0^t\sqrt{\frac{1-k^2x^2}{1-x^2}}\,dx \end{aligned}\] という定積分で表せる. この形の定積分は「第二種楕円積分」(Elliptic integral of the second kind) と呼ばれ,「初等関数」では表せないことが知られている.
※$2022/06/24$「初等関数」の定義を修正
