多面体
正多面体
定義《正多面体》
すべての面が合同な正多角形であり, すべての頂点において接する面の数が等しい多面体を正多面体 (regular polyhedron) と呼ぶ.
そのうち凹みがないものを凸正多面体と呼ぶ.
注意
凸正多面体を単に正多面体と呼ぶことも多い.
定理《正多面体の種類》
正多面体は, 正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体の $5$ つに限る.
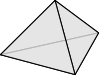
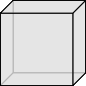
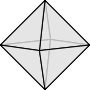
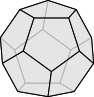





証明
こちらを参照.
高校数学の問題
図形と計量
問題《正多面体の外接球の半径》
$1$ 辺の長さが $1$ の正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体において, 最長対角線の長さ, 外接球の半径をそれぞれ求めよ.
ただし, $1$ 辺の長さが $1$ の正五角形の対角線の長さが「黄金数」
\[\varphi = \frac{1+\sqrt 5}{2}\]
であること (こちらとこちらを参照) は, 証明なしに使ってよい.
解答例
こちらを参照.
問題《正多面体の内接球の半径》
$1$ 辺の長さが $1$ の正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体において, 内接球の半径をそれぞれ求めよ.
ただし, 前問の結果は証明なしに使ってよい.
解答例
こちらを参照.
問題《正多面体の表面積》
$1$ 辺の長さが $1$ の正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体において, 表面積をそれぞれ求めよ.
ただし,
\[\sin 36^\circ = \frac{\sqrt{10-2\sqrt 5}}{4}, \quad \sin 72^\circ = \frac{\sqrt{10+2\sqrt 5}}{4}\]
であることは, 証明なしに使ってよい.
解答例
こちらを参照.
問題《正多面体の体積》
$1$ 辺の長さが $1$ の正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体において, 体積をそれぞれ求めよ.
$1$ 辺の長さが $1$ の正五角形の面積が $\dfrac{\sqrt{25+10\sqrt 5}}{4}$ であること,
および正四面体, 正八面体, 正十二面体, 正二十面体の内接球の半径がそれぞれ $\dfrac{\sqrt 6}{12},$ $\dfrac{\sqrt 6}{6},$ $\dfrac{1}{2}\sqrt{\dfrac{25+11\sqrt 5}{10}},$ $\dfrac{3\sqrt 3+\sqrt{15}}{12}$ であること (こちらを参照) は,
証明なしに使ってよい.
解答例
こちらを参照.
図形の性質
問題《正多面体の種類》
- (1)
- 各面が正 $p$ 角形であり, 各頂点に $q$ 本の辺が集まるような正多面体 (凸多面体) について, $(p-2)(q-2) < 4$ が成り立つことを示せ.
- (2)
- 正多面体 (凸多面体) は, 正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体の $5$ つに限ることを示せ.
解答例
こちらを参照.
ベクトル
問題《対辺が互いに垂直な等面四面体》
四面体 $\mathrm{OABC}$ が, $2$ つの条件
- (i)
- $\mathrm{OA} \perp \mathrm{BC},$ $\mathrm{OB} \perp \mathrm{CA},$ $\mathrm{OC} \perp \mathrm{AB}$
- (ii)
- $4$ つの面の面積がすべて等しい
(参考: $2003$ 京都大)
解答例
こちらを参照.