平面上の点
平面上の点
定理《$2$ 点間の距離の公式》
座標平面上の $2$ 点 $(x_1,y_1),$ $(x_2,y_2)$ の間の距離 $d$ は,
\[ d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\]
である.
問題《距離の公式による中線定理の証明》
$\triangle\mathrm{ABC}$ において, 辺 $\mathrm{BC}$ の中線を $\mathrm M$ とおく.
\[\mathrm{AB}^2+\mathrm{AC}^2 = 2(\mathrm{AM}^2+\mathrm{BM}^2) = 2(\mathrm{AM}^2+\mathrm{CM}^2)\]
が成り立つことを, $2$ 点間の距離の公式を使って示せ.
解答例
点 $\mathrm M$ を原点, 半直線 $\mathrm{MC}$ を $x$ 軸の $0$ 以上の部分として, $x$ 軸, $y$ 軸を定める.
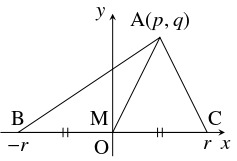$\mathrm A(p,q),$ $\mathrm C(r,0)$ とおくと, $\mathrm B(-r,0)$ となるから,
\[\begin{aligned}
\mathrm{AB}^2+\mathrm{AC}^2 &= \{ (p+r)^2+q^2\} +\{ (p-r)^2+q^2\} \\
&= 2\{ (p^2+q^2)+r^2\} \\
&= 2(\mathrm{AM}^2+\mathrm{BM}^2) = 2(\mathrm{AM}^2+\mathrm{CM}^2)
\end{aligned}\]
が成り立つ.
参考
問題《シュタインハウスの問題》
$xy$ 平面において $x$ 座標, $y$ 座標が整数である点を「格子点」と呼ぶ.
点 $\mathrm C\left(\sqrt 2,\dfrac{1}{3}\right)$ からそれぞれの「格子点」までの距離はすべて異なることを示せ.
$\sqrt 2$ が無理数であることは証明なしに使ってよい.
(参考: $1977$ 香川大)
解答例
$\mathrm P(x,y),$ $\mathrm P'(x',y')$ を「格子点」とし, $\mathrm{CP} = \mathrm{CP}'$ として, $\mathrm P = \mathrm P'$ を示す.
このとき, $\mathrm{CP}^2 = \mathrm{CP}'{}^2$ から,
\[ (x-\sqrt 2)^2+\left( y-\frac{1}{3}\right) ^2 = (x'-\sqrt 2)^2+\left( y'-\frac{1}{3}\right) ^2\]
が成り立つ.
両辺を展開して整理すると,
\[ 2(x-x')\sqrt 2 = x^2-x'{}^2+y^2-y'{}^2-\frac{2}{3}(y-y')\]
となる.
$\sqrt 2$ が無理数で $x,$ $x'$ が整数であるから, 左辺は $0$ か無理数である.
一方, $x,$ $y,$ $x',$ $y'$ は整数であるから, 右辺は有理数である.
よって, $x-x' = 0$ つまり $x = x'$ である.
このとき,
\[ 0 = y^2-y'{}^2-\frac{2}{3}(y-y') = \left( y+y'-\frac{2}{3}\right) (y-y')\]
となる.
$y+y'$ が整数であることから $y+y'-\dfrac{2}{3} \neq 0$ であり, $y-y' = 0$ から $y = y'$ が得られる.
よって, $\mathrm P = \mathrm P'$ である.
ゆえに, 点 $\mathrm C$ からそれぞれの「格子点」までの距離はすべて異なる.
ゆえに, 点 $\mathrm C$ からそれぞれの「格子点」までの距離はすべて異なる.
参考
- すべての正の整数 $n$ に対して, ちょうど $n$ 個の「格子点」を含むような円は存在するかという「シュタインハウスの問題」は, $1957$ 年にシュタインハウス (H. Steinhaus) によって提起され, 上記の命題を示すことでシェルピンスキー (W. Sierpinski) によって肯定的に解決された. つまり, 点 $\mathrm C$ を中心とする円の半径を大きくしていくと, 円に含まれる「格子点」は $1$ 個ずつ増えていく.
- これとは別に, ちょうど $n$ 個の「格子点」を通る円周は存在するかという問題も, $1958$ 年にシンゼル (A. Schinzel) によって肯定的に解決されている.