$2$ 次方程式
$2$ 次方程式
定理《$2$ 次方程式の解の公式》
実数係数 $2$ 次方程式 $ax^2+bx+c = 0$ $(a \neq 0)$ の解は
\[ x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
である.
証明
\[\begin{aligned}
&ax^2+bx+c = 0 \\
&\iff a\left( x+\frac{b}{2a}\right) ^2 = \frac{b^2-4ac}{4a} \\
&\iff \left( x+\frac{b}{2a}\right) ^2 = \frac{b^2-4ac}{4a^2} \\
&\iff x+\frac{b}{2a} = \pm\frac{\sqrt{b^2-4ac}}{2a} \\
&\iff x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{aligned}\]
から, 求める結果が得られる.
問題《チルンハウス変換による $2$ 次方程式の解法》
$2$ 次方程式 $ax^2+bx+c = 0\ \cdots [1]$ ($a,$ $b,$ $c$: 実数) について, $b^2-4ac \geqq 0$ であるとする.
$x = y-\dfrac{b}{2a}\ \cdots [2]$ とする.
- (1)
- $[1]$ に $[2]$ を代入することにより, $y$ の $2$ 次方程式を導け.
- (2)
- $2$ 次方程式の解の公式を示せ.
解答例
- (1)
- $[2]$ のもとで, \[\begin{aligned} &[1] \iff x^2+\frac{b}{a}x+\frac{c}{a} = 0 \\ &\iff \left( y-\frac{b}{2a}\right) ^2+\frac{b}{a}\left( y-\frac{b}{2a}\right) +\frac{c}{a} = 0 \\ &\iff \left( y^2-\frac{b}{a}y+\frac{b^2}{4a^2}\right)\!+\!\left(\frac{b}{a}y-\frac{b^2}{2a^2}\right)\!+\frac{c}{a} = 0 \\ &\iff y^2-\frac{b^2-4ac}{4a^2} = 0 \quad \cdots [1]' \end{aligned}\] が成り立つ.
- (2)
- \[\begin{aligned} &[1]' \iff y^2 = \frac{b^2-4ac}{4a^2} \\ &\iff y = \pm\frac{\sqrt{b^2-4ac}}{2a} \\ &\iff x+\frac{b}{2a} = \pm\frac{\sqrt{b^2-4ac}}{2a} \\ &\iff x = \frac{-b\pm\sqrt{b^2-4ac}}{2a} \end{aligned}\] から, $2$ 次方程式の解の公式が示された.
参考
$x$ の $n$ 次方程式 $a_nx^n+a_{n-1}x^{n-1}+\cdots +a_0 = 0$ に $x = y-\dfrac{a_{n-1}}{na_n}$ を代入すると, $f(x) = 0$ と同値な, $n-1$ 次の項が $0$ である $y$ の $n$ 次方程式が得られる.
この変数の置き換え $x = y-\dfrac{a_{n-1}}{na_n}$ は, 「チルンハウス変換」(Tschirnhaus transformation) と呼ばれ, $3$ 次方程式, $4$ 次方程式の解法で重要な役割を果たす.
問題《黄金長方形》
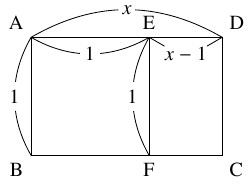
$1 = \mathrm{AB} < \mathrm{AD}$ なる長方形 $\mathrm{ABCD}$ から正方形 $\mathrm{ABFE}$ を切り取ってできる長方形 $\mathrm{DEFC}$ がもとの長方形 $\mathrm{ABCD}$ と相似になるとき,
辺 $\mathrm{AD}$ の長さ $x$ を求めよ.
ただし, $\mathrm E,$ $\mathrm F$ はそれぞれ辺 $\mathrm{AD},$ $\mathrm{BC}$ 上の点である.
解答例
仮定から $\mathrm{AB}:\mathrm{AD} = \mathrm{DE}:\mathrm{DC}$ つまり $1:x = (x-1):1$ であるので, $x(x-1) = 1^2$ から
\[ x^2-x-1 = 0\]
が成り立つ.
 よって, 解の公式により
\[ x = \dfrac{1+\sqrt 5}{2}\]
である ($x > 0$ に注意).
よって, 解の公式により
\[ x = \dfrac{1+\sqrt 5}{2}\]
である ($x > 0$ に注意).

参考
短辺と長辺の比が, 長辺から短辺を引いた差と短辺の比に等しいような長方形を「黄金長方形」(golden rectangle) と呼び,
その辺の長さの比 $1:\dfrac{1+\sqrt 5}{2}$ (約 $3:5$) を「黄金比」(golden ratio) と呼ぶ.
「黄金比」は最も美しい比であると言われ, 多くの美術作品の中にこの比を見ることができる.
問題《複 $2$ 次方程式》
$x^4-5x^2+5 = 0$ の解を求めよ.
解答例
与式を変形すると,
\[\begin{aligned}
x^4-2\cdot\frac{5}{2}x^2+\left(\frac{5}{2}\right) ^2 &= -5+\left(\frac{5}{2}\right) ^2 \\
\left( x^2-\frac{5}{2}\right) ^2 &= \frac{5}{4} \\
x^2-\frac{5}{2} &= \pm\frac{\sqrt 5}{2} \\
x^2 &= \frac{5\pm\sqrt 5}{2}
\end{aligned}\]
となるから, 求める解は
\[ x = \pm\sqrt{\frac{5\pm\sqrt 5}{2}} = \pm\frac{\sqrt{10\pm 2\sqrt 5}}{2}\]
である.
参考
$1$ 辺の長さが $1$ である正二十面体の最長対角線の長さは $\dfrac{\sqrt{10+2\sqrt 5}}{2}$ である (こちらを参照).
