関数の最大・最小 (理系)
関数の最大・最小
問題《点と曲線を結ぶ最短の線分と接線の関係》
実数値関数 $f(x)$ が $x = t$ を含むある開区間で微分可能であり,
曲線 $C:y = f(x)$ の上の点 $\mathrm T$ が $C$ 上にない定点 $\mathrm A$ から最短の距離にあるとする.
線分 $\mathrm{AT}$ と $C$ の点 $\mathrm T$ における接線は互いに垂直であることを示せ.
解答例
$\mathrm A(a,b),$ $\mathrm T(t,f(t))$ とおき, $C:y = f(x)$ 上の点 $\mathrm P(x,f(x))$ をとる.
\[\mathrm{AP}^2 = (x-a)^2+\{ f(x)-b\} ^2\]
の右辺を $g(x)$ とおく.
$\mathrm{AP}$ は $x = t$ のとき最小となるから, $g(x)$ は $x = t$ において極値をとる.
\[ g'(x) = 2(x-a)+2\{ f(x)-b\} f'(x)\]
であるので, $g'(t) = 0$ から
\[ (t-a)+\{ f(t)-b\} f'(t) = 0\]
が得られる.
$\mathrm A \neq \mathrm T$ から $t \neq a$ であるので,
\[\frac{f(t)-b}{t-a}\cdot f'(t) = -1\]
が成り立つ.
これは, 線分 $\mathrm{AT}$ と $y = f(x)$ の点 $\mathrm T$ における接線が互いに垂直であることを意味する.
問題《座標軸に接する線分の通過範囲》
- (1)
- $x$ を $0 < x < 1$ なる実数とする. このとき, $x$ を用いて $\theta$ の関数 \[ y = \sin\theta -x\tan\theta \quad \left( 0 < \theta < \dfrac{\pi}{2}\right)\] の最大値を表せ.
- (2)
- $x$ 軸, $y$ 軸に接する長さ $1$ の線分の通過範囲を求めよ.
解答例
- (1)
- \[\frac{dy}{d\theta} = \cos\theta -\frac{x}{\cos ^2\theta} = \frac{\cos ^3\theta -x}{\cos ^2\theta}\]
であるから, $\dfrac{dy}{d\theta} = 0$ つまり $\cos ^3\theta = x$ を満たす $\theta$ $\left( 0 < \theta < \dfrac{\pi}{2}\right)$ の値を $\alpha$ とおく.
このとき,
\[\frac{dy}{d\theta} \geqq 0 \iff \theta \leqq \alpha, \quad \frac{dy}{d\theta} \leqq 0 \iff \theta \geqq \alpha\]
であるから, $y$ は $\theta = \alpha$ の場合に限って, 極大かつ最大の値をとる.
$\cos ^3\alpha = x$ から \[\cos\alpha = x^{\frac{1}{3}}, \quad \sin\alpha = (1-x^{\frac{2}{3}})^{\frac{1}{2}}\] であるので, $y$ の最大値は \[\begin{aligned} \sin\alpha -x\tan\alpha &= (1-x^{\frac{2}{3}})^{\frac{1}{2}}-x\cdot\frac{(1-x^{\frac{2}{3}})^{\frac{1}{2}}}{x^{\frac{1}{3}}} \\ &= (1-x^{\frac{2}{3}})(1-x^{\frac{2}{3}})^{\frac{1}{2}} \\ &= (1-x^{\frac{2}{3}})^{\frac{3}{2}} \end{aligned}\] である.
$\theta$ $0$ $\cdots$ $\alpha$ $\cdots$ $\dfrac{\pi}{2}$ $\dfrac{dy}{d\theta}$ $+$ $0$ $-$ $y$ $\nearrow$ 極大 $\searrow$ - (2)
- 点 $(x,y)$ $(0 < x < 1,$ $0 < y < 1)$ が $x$ 軸, $y$ 軸に接する長さ $1$ の線分の通過範囲にあることは,
\[ y = \sin\theta -x\tan\theta\]
を満たす $\theta$ $\left( 0 < \theta < \dfrac{\pi}{2}\right)$ の存在と同値で, これは (1) の結果から
と同値である.
$y \leqq (1-x^{\frac{2}{3}})^{\frac{3}{2}}$ つまり $x^{\frac{2}{3}}+y^{\frac{2}{3}} \leqq 1$ 求める範囲は, $x$ 軸の $0 \leqq x \leqq 1$ の部分, $y$ 軸の $0 \leqq y \leqq 1$ の部分を含み, $x$ 軸, $y$ 軸に関して対称であるから, 不等式 \[ x^{\frac{2}{3}}+y^{\frac{2}{3}} \leqq 1\] を満たす点 $(x,y)$ 全体である.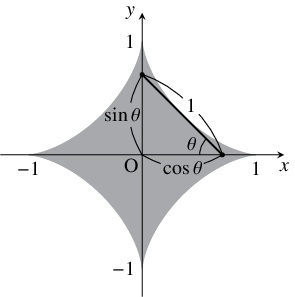
参考
- $x^{\frac{2}{3}}+y^{\frac{2}{3}} \leqq a^{\frac{2}{3}}$ で表される領域または曲線 $x^{\frac{2}{3}}+y^{\frac{2}{3}} = a^{\frac{2}{3}}$ $(a > 0)$ を星芒形またはアストロイド (astroid) と呼ぶ (小惑星を意味するアステロイドではなく, アストロイドと呼ぶ方が好ましい).
- $t$ がさまざまな値をとるとき, $x,$ $y$ の方程式 $f(x,y,t) = 0$ で表される曲線すべてに接する定曲線を, それらの曲線の「包絡線」(envelope) と呼ぶ. 本問において, 曲線 $x^{\frac{2}{3}}+y^{\frac{2}{3}} = a^{\frac{2}{3}}$ は $x$ 軸と $y$ 軸に接する長さ $a$ の線分の「包絡線」である.
- 曲線 $x^{\frac{2}{3}}+y^{\frac{2}{3}} = a^{\frac{2}{3}}$ は, 半径 $a$ の円の上をその周に沿って半径 $\dfrac{a}{4}$ の円がすべることなく転がるとき, 動円の周上の $1$ 点の軌跡としても定まる (こちらを参照).
問題《廊下を通過できる棒の長さの最大値》
幅 $x,$ $y$ の通路が直角につながった廊下を, 水平に保ったまま通過できる棒の長さの最大値を求めよ.
ただし, 通路は十分に長いとし, 棒の太さは無視して考えよ.
(参考: 東京工業大)
解答例
角を通過するとき, 長さが最大の棒は, 曲がり角, 幅 $x$ の通路の壁, 幅 $y$ の通路の壁の $3$ 点で廊下に接する.
このような棒のうち角を通過できるのは長さが最小のものであるから, その最小値を求めればよい.
棒が $3$ 点で廊下に接するとして, 棒と幅 $y$ の通路のなす鋭角を $\theta$ とおき, 棒の長さを $f(\theta )$ とおく.
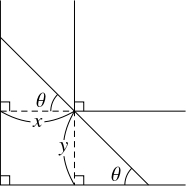 棒を曲がり角で $2$ つに分けると, 棒の長さは
\[ f(\theta ) = \frac{x}{\cos\theta}+\frac{y}{\sin\theta}\]
と表される.
\[ f'(\theta ) = \frac{x\sin\theta}{\cos ^2\theta}-\frac{y\cos\theta}{\sin ^2\theta} = \frac{x\sin ^3\theta -y\cos ^3\theta}{\sin ^2\theta\cos ^2\theta}\]
であるから,
\[\cos\alpha = \frac{x^{\frac{1}{3}}}{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}, \quad \sin\alpha = \frac{y^{\frac{1}{3}}}{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}\]
なる鋭角 $\alpha$ について
\[ f(\theta ) \geqq 0 \iff \theta \geqq \alpha, \quad f(\theta ) \leqq 0 \iff \theta \leqq \alpha\]
が成り立つ.
棒を曲がり角で $2$ つに分けると, 棒の長さは
\[ f(\theta ) = \frac{x}{\cos\theta}+\frac{y}{\sin\theta}\]
と表される.
\[ f'(\theta ) = \frac{x\sin\theta}{\cos ^2\theta}-\frac{y\cos\theta}{\sin ^2\theta} = \frac{x\sin ^3\theta -y\cos ^3\theta}{\sin ^2\theta\cos ^2\theta}\]
であるから,
\[\cos\alpha = \frac{x^{\frac{1}{3}}}{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}, \quad \sin\alpha = \frac{y^{\frac{1}{3}}}{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}\]
なる鋭角 $\alpha$ について
\[ f(\theta ) \geqq 0 \iff \theta \geqq \alpha, \quad f(\theta ) \leqq 0 \iff \theta \leqq \alpha\]
が成り立つ.
よって,
$f(\theta )$ は $\theta = \alpha$ のとき極小かつ最小の値
\[\begin{aligned}
f(\alpha ) &= \frac{x}{\cos\alpha}+\frac{y}{\sin\alpha} = x\cdot\frac{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}{x^{\frac{1}{3}}}+y\cdot\frac{\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}}}{y^{\frac{1}{3}}} \\
&= (x^{\frac{2}{3}}+y^{\frac{2}{3}})\sqrt{x^{\frac{2}{3}}+y^{\frac{2}{3}}} = (x^{\frac{2}{3}}+y^{\frac{2}{3}})^{\frac{3}{2}}
\end{aligned}\]
をとる.
ゆえに, 求める棒の長さの最大値は $(x^{\frac{2}{3}}+y^{\frac{2}{3}})^{\frac{3}{2}}$ である.

| $\theta$ | $0$ | $\cdots$ | $\alpha$ | $\cdots$ | $\dfrac{\pi}{2}$ |
| $f'(\theta )$ | $-$ | $0$ | $+$ | ||
| $f(\theta )$ | $\searrow$ | 極小 | $\nearrow$ |
参考
棒の長さが $a$ で一定であるとすると, 通路の幅 $x,$ $y$ は
を満たす.
この方程式が表す曲線は, 前問で扱ったアストロイドである.
| $(x^{\frac{2}{3}}+y^{\frac{2}{3}})^{\frac{3}{2}} = a$ つまり $x^{\frac{2}{3}}+y^{\frac{2}{3}} = a^{\frac{2}{3}}$ |
問題《正方形の頂点の最小シュタイナー木問題》
$xy$ 平面上に $4$ 点 $\mathrm A(1,1),$ $\mathrm B(−1,1),$ $\mathrm C(−1,−1),$ $\mathrm D(1,−1)$ をとる.
また, $y$ 軸に関して対称になるように, $x$ 軸上に点 $\mathrm P,$ $\mathrm Q$ をとる.
このとき, $L = \mathrm{PQ}+\mathrm{PA}+\mathrm{QB}+\mathrm{QC}+\mathrm{PD}$ の最小値と, 最小値を与える点 $\mathrm P$ の座標を求めよ.
ただし, 点 $\mathrm P$ の $x$ 座標は $0$ 以上 $1$ 以下であるとする.
(参考: $2015$ 早稲田大)
解答例
対称性により, $L$ の最小値は関数 $f(x) = \mathrm{PO}+\mathrm{PA}+\mathrm{PD} = \mathrm{PO}+2\mathrm{PA}$ の最小値の $2$ 倍である.
$x \geqq 0$ のとき,
\[\begin{aligned}
f(x) &= x+2\sqrt{(1-x)^2+(1-0)^2} = x+2\sqrt{x^2-2x+2}, \\
f'(x) &= 1+\frac{2x-2}{\sqrt{x^2-2x+2}} = \frac{2(x-1)+\sqrt{x^2-2x+2}}{\sqrt{x^2-2x+2}}
\end{aligned}\]
から,
\[\begin{aligned}
f'(x) = 0 &\iff 2(1-x) = \sqrt{x^2-2x+2} \\
&\ \ \Longrightarrow\; 4(1-x)^2 = x^2-2x+2 \\
&\iff 3x^2-6x+2 = 0 \\
&\ \ \Longrightarrow\; x = 1-\frac{1}{\sqrt 3}
\end{aligned}\]
が成り立つ.
よって, $f(x)$ の増減表は次の通りであるから,
$f(x)$ は $x = 1-\dfrac{1}{\sqrt 3}$ のとき極小かつ最小の値 $1+\sqrt 3$ をとる.
最小値は, 点 $\mathrm P$ から辺 $\mathrm{AD}$ に下ろした垂線の足 $\mathrm H$ について,
$\mathrm{AH}:\mathrm{HP} = 1:\dfrac{1}{\sqrt 3} = \sqrt 3:1$ から $\mathrm{PA} = \dfrac{2}{\sqrt 3}$ であることを使って
\[\left( 1-\frac{1}{\sqrt 3}\right) +2\cdot\frac{2}{\sqrt 3} = 1+\frac{3}{\sqrt 3} = 1+\sqrt 3\]
と求めた.
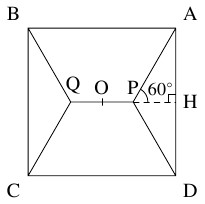 ゆえに, $L$ は $\mathrm P\left( 1-\dfrac{1}{\sqrt 3},0\right)$ のとき最小値 $2(1+\sqrt 3)$ をとる.
ゆえに, $L$ は $\mathrm P\left( 1-\dfrac{1}{\sqrt 3},0\right)$ のとき最小値 $2(1+\sqrt 3)$ をとる.
| $x$ | $0$ | $\cdots$ | $1-\dfrac{1}{\sqrt 3}$ | $\cdots$ | $1$ |
| $f'(x)$ | $-$ | $0$ | $+$ | ||
| $f(x)$ | $\searrow$ | $1+\sqrt 3$ | $\nearrow$ |

参考
- 正方形の頂点を結ぶ最短経路を求める問題は「三角不等式」$\mathrm P\mathrm P'+\mathrm P'\mathrm P'' \geqq \mathrm P\mathrm P''$ を使った議論により本問のような場合に帰着されて (詳細は省略), その解は上の図の通りである.
- なお, 正五角形の頂点を結ぶ最短経路は次の図の通りであること ($3$ つの三叉路を結んだ経路で, $2$ 辺のなす角はすべて $120^\circ$),
$n \geqq 6$ のとき正 $n$ 角形 $\mathrm P_1\mathrm P_2\cdots\mathrm P_n$ の頂点を結ぶ最短経路は折れ線 $\mathrm P_1\mathrm P_2\cdots\mathrm P_n$ であることが知られている.
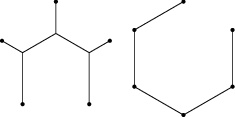
- 分岐点を新たに設けてもよいという条件の下で, 与えられたいくつかの点をもれなく結ぶ最短経路は「最小シュタイナー木」と呼ばれ, その求め方としていくつかの初等幾何学的なアルゴリズムが知られている.
問題《円に内接する三角形の面積の最大値》
単位円に内接する三角形 $T$ の面積を $S$ とおく.
- (1)
- $T$ の内角を $x,$ $y,$ $z$ とおく. \[ S = 2\sin x\sin y\sin z\] であることを示せ.
- (2)
- $S$ の最大値を求めよ.
(参考: $1986$ お茶の水女子大)
解答例
- (1)
- $\mathrm{BC} = a,$ $\mathrm{CA} = b,$ $\angle\mathrm A = x,$ $\angle\mathrm B = y,$ $\angle\mathrm C = z$ なる $T = \triangle\mathrm{ABC}$ を考える. 正弦定理により \[ a = 2\sin x, \quad b = 2\sin y\] であるから, \[\begin{aligned} S &= \frac{1}{2}ab\sin z \\ &= \frac{1}{2}\cdot 2\sin x\cdot 2\sin y\cdot\sin z \\ &= 2\sin x\sin y\sin z \end{aligned}\] が成り立つ.
- (2)
- (1) と $z = \pi -x-y$ から,
\[\begin{aligned}
S = &2\sin x\sin y\sin (x+y) \\
&\quad (0 < x < \pi,\ 0 < y < \pi,\ 0 < x+y < \pi)
\end{aligned}\]
が成り立つ.
まず, $y$ を定数とみなして,
\[ f(x) = 2\sin y\sin x\sin (x+y)\]
の最大値を求める.
\[\begin{aligned}
f'(x) &= 2\sin y\{\cos x\sin (x+y)+\sin x\cos (x+y)\} \\
&= 2\sin y\sin (2x+y)
\end{aligned}\]
であり, $0 < y < \pi$ から $\sin y > 0$ であるので,
\[\begin{aligned}
f'(x) \geqq 0 &\iff \sin (2x+y) \geqq 0 \\
&\iff 2x+y \leqq \pi \iff x \leqq \frac{\pi -y}{2}, \\
f'(x) \leqq 0 &\iff x \geqq \frac{\pi -y}{2}
\end{aligned}\]
が成り立つ ($0 < 2x+y < 2\pi$ に注意).
よって, $f(x)$ は $x = \dfrac{\pi -y}{2}$ の場合に限って, 極大かつ最大の値 \[\begin{aligned} f\left(\frac{\pi -y}{2}\right) &= 2\sin y\sin\frac{\pi +y}{2}\sin\frac{\pi -y}{2} \\ &= 2\sin y\cos ^2\frac{y}{2} = \sin y(1+\cos y) \end{aligned}\] をとる (余角公式, 半角の公式による). そこで, $x = \dfrac{\pi -y}{2}$ のもとで, この式を $g(y)$ とおき, その最大値を求める. \[\begin{aligned} g'(y) &= \cos y(1+\cos y)-\sin ^2y \\ &= 2\cos ^2y+\cos y-1 \\ &= (\cos y+1)(2\cos y-1) \end{aligned}\] であり, $0 < y < \pi$ から $\cos y+1 > 0$ であるので, \[\begin{aligned} g'(y) \geqq 0 &\iff 2\cos y-1 \geqq 0 \\ &\iff \cos y \geqq \frac{1}{2} \iff y \leqq \frac{\pi}{3}, \\ g'(y) \leqq 0 &\iff y \geqq \frac{\pi}{3}, \\ \end{aligned}\] が成り立つ.
$x$ $0$ $\cdots$ $\dfrac{\pi -y}{2}$ $\cdots$ $\pi$ $f'(x)$ $+$ $0$ $-$ $f(x)$ $\nearrow$ 極大 $\searrow$ よって, $g(y)$ は $y = \dfrac{\pi}{3}$ の場合に限って, 極大かつ最大の値 \[\begin{aligned} g\left(\frac{\pi}{3}\right) &= \sin\frac{\pi}{3}\left( 1+\cos\frac{\pi}{3}\right) \\ &= \frac{\sqrt 3}{2}\left( 1+\frac{1}{2}\right) = \frac{3\sqrt 3}{4} \end{aligned}\] をとる. このとき, \[ x = \frac{\pi-y}{2} = \frac{\pi}{3}, \quad z = \pi -x-y = \frac{\pi}{3}\] である. ゆえに, $x = y = z = \dfrac{\pi}{3}$ のとき, $S$ は最大値 $\dfrac{3\sqrt 3}{4}$ をとる.$y$ $0$ $\cdots$ $\dfrac{\pi}{3}$ $\cdots$ $\pi$ $g'(y)$ $+$ $0$ $-$ $g(y)$ $\nearrow$ 極大 $\searrow$
別解
- (2)
- (1) と $z = \pi -x-y$ から, \[\begin{aligned} S &= 2\sin y\sin (x+y)\sin x \\ &= 2\sin y\cdot\frac{\cos (x+y-x)-\cos (x+y+x)}{2} \\ &= \sin y\{\cos y-\cos (2x+y)\} \\ &\qquad (0 < x < \pi,\ 0 < y < \pi,\ 0 < x+y < \pi ) \end{aligned}\] が成り立つ. また, $0 < 2x+y < 2\pi$ であるから, $S$ は $x$ の関数として $\cos (2x+y) = -1$ つまり $2x+y = \pi$ のとき最大値 $\sin y(\cos y+1)$ をとる. 以下, 上記の解答例と同様.
参考
- 多変数関数 $f(x_1,\cdots,x_n)$ について, ある変数 $x_k$ 以外の変数を定数とみなして, $f(x_1,\cdots,x_n)$ を $x_k$ で微分することを「偏微分」(partial derivative) という. 「偏微分」により, $1$ 変数関数の微分法を拡張して, さまざまな関数が調べられる.
- $3$ 変数の相加・相乗平均の不等式 (例えばこちらを参照) を使い, $\sin x$ $(0 < x < \pi )$ に「イェンゼンの不等式」(こちらを参照) を適用すると, \[\begin{aligned} S &= 2\sin x\sin y\sin z \\ &\leqq 2\left(\frac{\sin x+\sin y+\sin z}{3}\right) ^3 \\ &\leqq 2\sin ^3\frac{x+y+z}{3} \\ &= 2\sin ^3\frac{\pi}{3} = 2\left(\frac{\sqrt 3}{2}\right) ^3 \\ &= \frac{3\sqrt 3}{4} \end{aligned}\] が得られる. 等号は $\sin x = \sin y = \sin z,$ $x = y = z$ のとき, つまり $x = y = z = \dfrac{\pi}{3}$ のとき成り立つ.
問題《与えられた辺長をもつ四角形の面積の最大値》
$a,$ $b,$ $c,$ $d$ を $4$ 辺の長さとする四角形のうち, 円に内接するものが存在するとする.
このとき, このような四角形の面積は, 四角形が円に内接するとき最大となることを示せ.
解答例
四角形 $\mathrm{ABCD}$ において, $a = \mathrm{AB},$ $b = \mathrm{BC},$ $c = \mathrm{CD},$ $d = \mathrm{DA},$ $\theta = \angle\mathrm{ABC},$ $\varphi = \angle\mathrm{CDA}$ とおき, 面積を $S$ とおく.
このとき,
\[ S = \frac{1}{2}ab\sin\theta +\frac{1}{2}cd\sin\varphi\]
が成り立つ.
$S$ を $\theta$ で微分すると,
\[\frac{dS}{d\theta} = \frac{1}{2}ab\cos\theta +\frac{1}{2}cd\cos\varphi\frac{d\varphi}{d\theta} \quad \cdots [1]\]
となる.
ここで, 余弦定理により
\[\mathrm{AC}^2 = a^2+b^2-2ab\cos\theta = c^2+d^2-2cd\cos\varphi\]
となるから, 両辺を $\theta$ で微分すると
\[ 2ab\sin\theta = 2cd\sin\varphi\frac{d\varphi}{d\theta} \quad \cdots [2]\]
となる.
$[2]$ を使って $[1]$ の $\dfrac{d\varphi}{d\theta}$ を消去して整理すると,
\[\frac{dS}{d\theta} = \frac{ab}{2\sin\varphi}\sin (\theta +\varphi )\]
が得られる.
$0 < \varphi < \pi,$ $0 < \theta +\varphi < 2\pi$ から,
\[\begin{aligned}
\frac{dS}{d\theta} \geqq 0 &\iff \theta +\varphi \leqq \pi, \\
\frac{dS}{d\theta} \leqq 0 &\iff \theta +\varphi \geqq \pi
\end{aligned}\]
が成り立つ.
よって, $S$ は $\theta +\varphi = \pi$ のとき, 極大かつ最大の値をとる.
ゆえに, 四角形が円に内接するとき, 四角形の面積は最大になる.
問題《体積が一定である円柱の表面積の最小値》
$V$ を正の数とする.
- (A)
- 体積が $V$ である直円柱の表面積 $S$ が最小になるとき, 底面の半径 $x$ と高さ $h$ の比, $V$ の値を求めよ.
- (B)
- 容積が $V$ である, ふたのない, 薄い直円柱の形をした容器の側面積と底面積の和 $S$ が最小になるとき, 底面の半径 $x$ と高さ $h$ の比, $V$ の値を求めよ. ただし, 側面積と底面積は, いずれも容器の外側のみを測るものとする.
解答例
- (A)
- $V = \pi x^2h$ であるから,
\[ h = \frac{V}{\pi x^2}\]
が成り立つ.
よって,
\[ S = 2\pi x^2+2\pi xh = 2\pi x^2+2\pi x\cdot\frac{V}{\pi x^2} = 2\pi x^2+\frac{2V}{x}\]
であるから
\[\frac{dS}{dx} = 4\pi x-\frac{2V}{x^2} = \frac{4\pi}{x^2}\left( x^3-\frac{V}{2\pi}\right)\]
であり,
\[\begin{aligned}
\frac{dS}{dx} \geqq 0 &\iff \sqrt[3]{\frac{V}{2\pi}} \leqq x, \\
\frac{dS}{dx} \leqq 0 &\iff 0 < x \leqq \sqrt[3]{\frac{V}{2\pi}}
\end{aligned}\]
が成り立つ ($x > 0$ に注意).
よって, $x = \sqrt[3]{\dfrac{V}{2\pi}}$ のとき, $S$ は極小かつ最小の値をとる. このとき, \[ h = V\div\pi\left(\sqrt[3]{\frac{V}{2\pi}}\right) ^2 = \sqrt[3]{\frac{4V}{\pi}} = 2\sqrt[3]{\frac{V}{2\pi}}\] から $x:h = 1:2$ であり, \[ S = 2\pi x^2\!+\!2\pi x\!\cdot\!2x = 6\pi x^2 = 6\pi\left(\sqrt[3]{\frac{V}{2\pi}}\right) ^2 = 3\sqrt[3]{2\pi V^2}\] である.
$x$ $0$ $\cdots$ $\sqrt[3]{\dfrac{V}{2\pi}}$ $\cdots$ $\dfrac{dS}{dx}$ $-$ $0$ $+$ $S$ $\searrow$ 極小 $\nearrow$ - (B)
- $V = \pi x^2h$ であるから,
\[ h = \frac{V}{\pi x^2}\]
が成り立つ.
よって,
\[ S = \pi x^2+2\pi xh = \pi x^2+2\pi x\cdot\frac{V}{\pi x^2} = \pi x^2+\frac{2V}{x}\]
であるから
\[\frac{dS}{dx} = 2\pi x-\frac{2V}{x^2} = \frac{2\pi}{x^2}\left( x^3-\frac{V}{\pi}\right)\]
であり,
\[\begin{aligned}
\frac{dS}{dx} \geqq 0 &\iff \sqrt[3]{\frac{V}{\pi}} \leqq x, \\
\frac{dS}{dx} \leqq 0 &\iff 0 < x \leqq \sqrt[3]{\frac{V}{\pi}}
\end{aligned}\]
が成り立つ ($x > 0$ に注意).
よって, $x = \sqrt[3]{\dfrac{V}{\pi}}$ のとき, $S$ は極小かつ最小の値をとる. このとき, \[ h = V\div\pi\left(\sqrt[3]{\frac{V}{\pi}}\right) ^2 = \sqrt[3]{\frac{V}{\pi}}\] から $x:h = 1:1$ であり, \[ S = \pi x^2+2\pi x\cdot x = 3\pi x^2 = 3\pi\left(\sqrt[3]{\frac{V}{\pi}}\right) ^2 = 3\sqrt[3]{\pi V^2}\] である.
$x$ $0$ $\cdots$ $\sqrt[3]{\dfrac{V}{\pi}}$ $\cdots$ $\dfrac{dS}{dx}$ $-$ $0$ $+$ $S$ $\searrow$ 極小 $\nearrow$
問題《体積が一定である円錐の表面積の最小値》
$V$ を正の数とする.
容積が $V$ である, ふたのない, 薄い直円錐の形をした容器の側面積 $S$ が最小になるとき,
底面の半径 $x$ と母線の長さ $y$ と高さ $h$ の比, $S$ の値を求めよ.
ただし, 側面積は, 容器の外側のみを測るものとする.
解答例
$V = \dfrac{1}{3}\pi x^2h$ であるから,
\[ h = \frac{3V}{\pi x^2}\]
が成り立つ.
よって,
\[ S = \frac{1}{2}\cdot 2\pi x\cdot y = \pi xy\]
から
\[\begin{aligned}
\frac{S^2}{\pi ^2} &= x^2y^2 = x^2(x^2+h^2) \\
&= x^2\left( x^2+\frac{9V^2}{\pi ^2x^4}\right) = x^4+\frac{9V^2}{\pi ^2x^2}
\end{aligned}\]
であるので, この右辺を $f(x)$ とおく.
\[ f'(x) = 4x^3-\frac{18V^2}{\pi ^2x^3} = \frac{4}{x^3}\left( x^6-\frac{9V^2}{2\pi ^2}\right)\]
であるから,
\[\begin{aligned}
f'(x) \geqq 0 &\iff \sqrt[6]{\frac{9V^2}{2\pi ^2}} \leqq x, \\
f'(x) \leqq 0 &\iff 0 < x \leqq \sqrt[6]{\frac{9V^2}{2\pi ^2}}
\end{aligned}\]
が成り立つ ($x > 0$ に注意).
よって, $x = \sqrt[6]{\dfrac{9V^2}{2\pi ^2}}$ のとき, $f(x)$ は極小かつ最小の値をとる.
このとき,
\[ h = 3V\div\pi\left(\sqrt[6]{\frac{9V^2}{2\pi ^2}}\right) ^2 = \sqrt 2\sqrt[6]{\frac{9V^2}{2\pi ^2}}\]
から $x:y:h = 1:\sqrt 3:\sqrt{2}$ であり,
\[ S = \pi x\cdot\sqrt 3x = \sqrt 3\pi x^2 = \sqrt 3\pi\left(\sqrt[6]{\frac{9V^2}{2\pi ^2}}\right) ^2 = 3\sqrt[6]{\frac{3\pi ^2V^4}{4}}\]
である.
| $x$ | $0$ | $\cdots$ | $\sqrt[6]{\dfrac{9V^2}{2\pi ^2}}$ | $\cdots$ |
| $f'(x)$ | $-$ | $0$ | $+$ | |
| $f(x)$ | $\searrow$ | 極小 | $\nearrow$ |
