関数の最大・最小 (文系・理系共通)
関数の最大・最小
定理《多項式関数の最大・最小》
閉区間 $a \leqq x \leqq b$ において, 多項式関数 $f(x)$ は必ず最大値, 最小値をもつ.
$a \leqq x \leqq b$ における $f(x)$ の最大値, 最小値は, $f(x)$ の極値, $f(a),$ $f(b)$ のいずれかである.
開区間における関数の最大値, 最小値を求める場合にも, 増減を調べることが重要である (最大値, 最小値をもたないこともある).
問題《チェビシェフ多項式に関する最大値》
- (1)
- 関数 $\left| x^3-\dfrac{3}{4}x\right|$ の $-1 \leqq x \leqq 1$ における最大値 $M_0$ を求めよ.
- (2)
- $a,$ $b,$ $c$ を実数とする. 関数 $|x^3+ax^2+bx+c|$ の $-1 \leqq x \leqq 1$ における最大値 $M$ は $M_0$ 以上であることを示せ.
解答例
- (1)
- $f_0(x) = x^3-\dfrac{3}{4}x$ $(-1 \leqq x \leqq 1)$ とおく.
このとき,
\[ f_0{}'(x) = 3x^2-\frac{3}{4} = 3\left( x+\frac{1}{2}\right)\left( x-\frac{1}{2}\right)\]
から
\[\begin{aligned}
&f_0{}'(x) \geqq 0 \iff x \leqq -\frac{1}{2},\ \frac{1}{2} \leqq x, \\
&f_0{}'(x) \leqq 0 \iff -\frac{1}{2} \leqq x \leqq \frac{1}{2}
\end{aligned}\]
となるので, $f_0(x)$ は $x = -\dfrac{1}{2}$ で極大値 $\dfrac{1}{4},$ $x = \dfrac{1}{2}$ で極小値 $-\dfrac{1}{4}$ をとる.
また, $f_0(-1) = -\dfrac{1}{4},$ $f(1) = \dfrac{1}{4}$ であるから, $f_0(x)$ は $x = 1,$ $-\dfrac{1}{2}$ で最大値 $\dfrac{1}{4},$ $x = -1,$ $\dfrac{1}{2}$ で最小値 $-\dfrac{1}{4}$ をとる. ゆえに, $|f_0(x)|$ の $-1 \leqq x \leqq 1$ における最大値は $M_0 = \dfrac{1}{4}$ である.
$x$ $-1$ $\cdots$ $-\dfrac{1}{2}$ $\cdots$ $\dfrac{1}{2}$ $\cdots$ $1$ $f_0{}'(x)$ $+$ $0$ $-$ $0$ $+$ $f_0(x)$ $\nearrow$ 極大 $\searrow$ 極小 $\nearrow$ 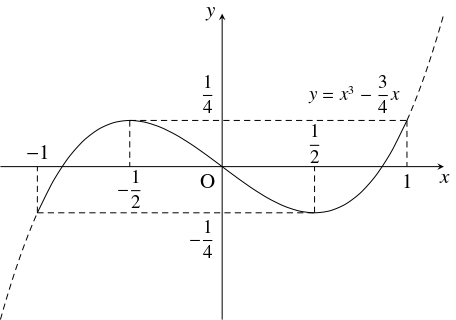
- (2)
- ある関数 $f(x) = x^3+ax^2+bx+c$ $(-1 \leqq x \leqq 1)$ について, $|f(x)|$ の最大値 $M$ が $M_0$ 未満であるとして矛盾を導く.
このとき, $|f(x)| \leqq M < M_0 = \dfrac{1}{4}$ から,
\[ f(\pm 1) < \frac{1}{4}, \quad -\frac{1}{4} < f\left(\pm\dfrac{1}{2}\right)\]
であるので,
\[\begin{aligned}
&\ a+b+c < -\frac{3}{4}, \quad \cdots [1] \\
&-a+b-c < -\frac{3}{4}, \quad \cdots [2] \\
&-\frac{3}{2} < a+2b+4c, \quad \cdots [3]\\
&-\frac{3}{2} < a+2b-4c \quad \cdots [4]
\end{aligned}\]
が成り立つ.
$[1]+[2]$ から $b < -\dfrac{3}{4},$ $[3]+[4]$ から $-\dfrac{3}{4} < b$ となるが, これは矛盾である.
ゆえに, 関数 $f(x) = x^3+ax^2+bx+c$ $(-1 \leqq x \leqq 1)$ について, $|f(x)|$ の最大値 $M$ は $M_0$ 以上である.
参考
一般に, $n$ 次の多項式関数について, 次の「チェビシェフの定理」(theorem of Chebyshev) が知られている:
$n$ 次の項の係数が $1$ である $n$ 次の多項式 $f(x)$ について, $-1 \leqq x \leqq 1$ における $|f(x)|$ の最大値 $M$ は $M \geqq \dfrac{1}{2^{n-1}}$ を満たす.
等号成立は, $f(x) = \dfrac{1}{2^{n-1}}T_n(x)$ の場合に限る.
ここで, $T_n(x)$ は, $n$ 次の「第一種チェビシェフの多項式」, つまり $T_n(\cos\theta ) = \cos n\theta$ を満たす多項式である.
問題《直方体の箱の容積の最大値》
$1$ 辺の長さが $1$ の正方形の紙の四隅から $1$ 辺の長さが $x$ の正方形を取り除き, その残りを折り曲げて, ふたのない高さ $x$ の直方体の箱を作る.
このとき, 箱の容積 $V$ の最大値を求めよ.
(参考: $2023$ 大学入学共通テスト追試)
解答例
底面の $1$ 辺の長さは $1-2x$ である.
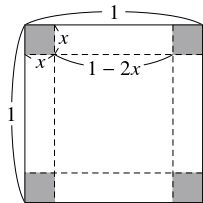 よって,
\[ V = x(1-2x)^2 = 4x^3-4x^2+x\]
であるから,
\[\frac{dV}{dx} = 12x^2-8x+1 = (2x-1)(6x-1)\]
であり,
\[\begin{aligned}
\frac{dV}{dx} \geqq 0 &\iff 0 < x \leqq \frac{1}{6}, \\
\frac{dV}{dx} \leqq 0 &\iff \frac{1}{6} \leqq x < \frac{1}{2}
\end{aligned}\]
が成り立つ ($0 < x < \dfrac{1}{2}$ に注意).
よって,
\[ V = x(1-2x)^2 = 4x^3-4x^2+x\]
であるから,
\[\frac{dV}{dx} = 12x^2-8x+1 = (2x-1)(6x-1)\]
であり,
\[\begin{aligned}
\frac{dV}{dx} \geqq 0 &\iff 0 < x \leqq \frac{1}{6}, \\
\frac{dV}{dx} \leqq 0 &\iff \frac{1}{6} \leqq x < \frac{1}{2}
\end{aligned}\]
が成り立つ ($0 < x < \dfrac{1}{2}$ に注意).
よって, $V$ は $x = \dfrac{1}{6}$ のとき極大かつ最大の値
\[\frac{1}{6}\left( 1-2\cdot\frac{1}{6}\right) ^2 = \frac{2}{27}\]
をとる.
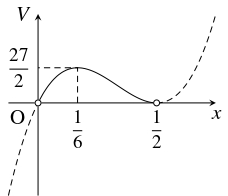

| $x$ | $0$ | $\cdots$ | $\dfrac{1}{6}$ | $\cdots$ | $\dfrac{1}{2}$ |
| $\dfrac{dV}{dx}$ | $+$ | $0$ | $-$ | ||
| $V$ | $\nearrow$ | 極大 | $\searrow$ |

参考
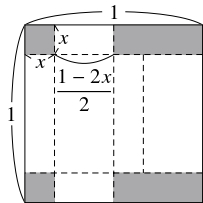
- 正方形の四隅から正方形 $2$ 個と長方形 $2$ 個を取り除き, その残りを折り曲げて, ふたのついた高さ $x$ $\left( 0 < x < \dfrac{1}{2}\right)$ の直方体の箱を作るとき,
底面の長方形の短い方の辺の長さはふたのない場合の半分になるから,
箱の容積の最大値はふたのない場合の半分の $\dfrac{1}{27}\ \left( x = \dfrac{1}{6}\right)$ である.
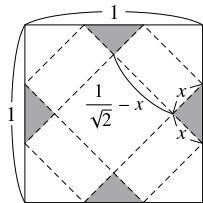
- 正方形の $4$ 辺に接する部分から $4$ 個の直角二等辺三角形を取り除き, その残りを折り曲げて, ふたのついた高さ $x$ $\left( 0 < x < \dfrac{1}{\sqrt 2}\right)$ の直方体の箱を作るとき, 箱の容積 $V$ は
\[ V = x\left(\frac{1}{\sqrt 2}-x\right)^2 = x^3-\sqrt 2x^2+\frac{1}{2}x,\]
$V$ の導関数は
\[\frac{dV}{dx} = 3x^2-2\sqrt 2x+\frac{1}{2} = 3\left( x-\frac{1}{3\sqrt 2}\right)\left( x-\frac{1}{\sqrt 2}\right)\]
であるから, $V$ の最大値は $\dfrac{1}{3\sqrt 2}\left(\dfrac{1}{\sqrt 2}-\dfrac{1}{3\sqrt 2}\right) ^2 = \dfrac{\sqrt 2}{27}$ $\left( x = \dfrac{1}{3\sqrt 2}\right)$ である.
問題《球に内接する三角柱の体積の最大値》
点 $\mathrm O$ を中心とする半径 $1$ の球に内接する正三角柱 $\mathrm{ABC}$-$\mathrm{DEF}$ において, 底面の $1$ 辺の長さを $a,$ 体積を $V$ とおき, $2\theta = \angle\mathrm{AOD}$ とおく.
- (1)
- $\theta$ を用いて $a$ を表せ.
- (2)
- $\theta$ を用いて $V$ を表せ.
- (3)
- $V$ の最大値を求めよ.
(参考: $2014$ 大阪市立大)
解答例
- (1)
- 辺 $\mathrm{AD}$ の中点を $\mathrm M,$ $\triangle\mathrm{ABC}$ の重心を $\mathrm G$ とおく. 直角三角形 $\mathrm{OAM}$ に着目すると \[\cos\theta = \cos\angle\mathrm{AOM} = \frac{\mathrm{OM}}{\mathrm{OA}} = \frac{\mathrm{AG}}{1} = \dfrac{2}{3}\cdot\frac{\sqrt 3}{2}a = \frac{a}{\sqrt 3}\] となるから, $a$ は \[ a = \sqrt 3\cos\theta\] と表せる.
- (2)
- この正三角柱の高さは $2\sin\theta$ であるから, 体積は \[\begin{aligned} V &= \frac{1}{2}a^2\sin 60^\circ\cdot 2\sin\theta \\ &= \frac{\sqrt 3}{2}\cdot (\sqrt 3\cos\theta )^2\cdot\sin\theta \\ &= \frac{3\sqrt 3}{2}\sin\theta\cos ^2\theta \end{aligned}\] と表せる.
- (3)
- $x = \sin\theta$ とおく.
\[\frac{2}{3\sqrt 3}V = \sin\theta (1-\sin ^2\theta ) = \sin\theta -\sin ^3\theta = x-x^3\]
であるから, この右辺を $f(x)$ とおく.
\[ f'(x) = 1-3x^2\]
であるから,
\[\begin{aligned}
f'(x) \geqq 0 &\iff 0 < x \leqq \frac{1}{\sqrt 3}, \\
f'(x) \leqq 0 &\iff \frac{1}{\sqrt 3} \leqq x < 1
\end{aligned}\]
が成り立つ ($0 < x < 1$ に注意).
よって, $f(x)$ は $x = \dfrac{1}{\sqrt 3}$ のとき極大かつ最大の値をとる. ゆえに, $V$ の最大値は \[\frac{3\sqrt 3}{2}\cdot\frac{1}{\sqrt 3}\left( 1-\frac{1}{3}\right) = 1\] である.
$x$ $0$ $\cdots$ $\dfrac{1}{\sqrt 3}$ $\cdots$ $1$ $f'(x)$ $+$ $0$ $-$ $f(x)$ $\nearrow$ 極大 $\searrow$
参考
円に内接する面積が最大の三角形は正三角形であるから, 半径 $1$ の球に内接する体積が最大の三角柱は正三角柱で, その体積は $1$ である.
問題《球に内接する円柱の体積の最大値》
半径 $1$ の球に内接する直円柱の体積 $V$ の最大値を求めよ.
解答例
半径 $1$ の球に内接する直円柱の底面の半径を $r,$ 高さを $x$ とおく.
 このとき, 円柱の底面の直径を通る断面を考えると, 三平方の定理により
\[ (2r)^2+x^2 = 2^2\]
となるから,
\[ r = \frac{1}{2}\sqrt{4-x^2}\]
である.
よって,
\[ V = \pi\left(\frac{1}{2}\sqrt{4-x^2}\right) ^2x = \frac{\pi}{4}(4x-x^3)\]
であるから,
\[\frac{dV}{dx} = \frac{\pi}{4}(4-3x^2) = -\frac{\pi}{4}(\sqrt 3x+2)(\sqrt 3x-2)\]
であり,
\[\begin{aligned}
\frac{dV}{dx} \geqq 0 &\iff 0 < x \leqq \frac{2}{\sqrt 3}, \\
\frac{dV}{dx} \leqq 0 &\iff \frac{2}{\sqrt 3} \leqq x < 2
\end{aligned}\]
が成り立つ ($0 < x < 2$ に注意).
このとき, 円柱の底面の直径を通る断面を考えると, 三平方の定理により
\[ (2r)^2+x^2 = 2^2\]
となるから,
\[ r = \frac{1}{2}\sqrt{4-x^2}\]
である.
よって,
\[ V = \pi\left(\frac{1}{2}\sqrt{4-x^2}\right) ^2x = \frac{\pi}{4}(4x-x^3)\]
であるから,
\[\frac{dV}{dx} = \frac{\pi}{4}(4-3x^2) = -\frac{\pi}{4}(\sqrt 3x+2)(\sqrt 3x-2)\]
であり,
\[\begin{aligned}
\frac{dV}{dx} \geqq 0 &\iff 0 < x \leqq \frac{2}{\sqrt 3}, \\
\frac{dV}{dx} \leqq 0 &\iff \frac{2}{\sqrt 3} \leqq x < 2
\end{aligned}\]
が成り立つ ($0 < x < 2$ に注意).
よって, $V$ は $x = \dfrac{2}{\sqrt 3}$ のとき極大かつ最大の値
\[\frac{\pi}{4}\left( 4-\frac{4}{3}\right)\cdot\frac{2\sqrt 3}{3} = \frac{4\sqrt 3}{9}\pi\]
をとる.

| $x$ | $0$ | $\cdots$ | $\dfrac{2}{\sqrt 3}$ | $\cdots$ | $2$ |
| $\dfrac{dV}{dx}$ | $+$ | $0$ | $-$ | ||
| $V$ | $\nearrow$ | 極大 | $\searrow$ |
問題《球に内接する円錐の体積の最大値》
半径 $1$ の球に内接する直円錐の体積 $V$ の最大値を求めよ.
解答例
半径 $1$ の球に内接する直円錐の底面の半径を $r,$ 高さを $x$ とおく.
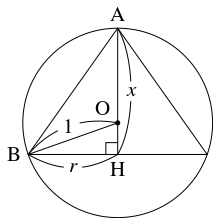 この円錐の頂点 $\mathrm A$ から底面に下ろした垂線 $\mathrm{AH}$ は球の中心 $\mathrm O$ を通り,
$\mathrm{AB}$ を円錐の母線とすると $\triangle\mathrm{OBH}$ は $\angle\mathrm H = 90^\circ$ なる直角三角形になるから,
\[\begin{aligned}
r^2 &= \mathrm{BH}^2 = \mathrm{OB}^2-\mathrm{OH}^2 \\
&= 1^2-(x-1)^2 = 2x-x^2
\end{aligned}\]
が成り立つ.
よって,
\[ V = \frac{1}{3}\cdot\pi r^2\cdot x = \frac{\pi}{3}(2x^2-x^3)\]
であるから,
\[\frac{dV}{dx} = \frac{\pi}{3}(4x-3x^2) = -\frac{\pi}{3}x(3x-4)\]
であり,
\[\begin{aligned}
\frac{dV}{dx} \geqq 0 &\iff 0 < x \leqq \frac{4}{3}, \\
\frac{dV}{dx} \leqq 0 &\iff \frac{4}{3} \leqq x < 2
\end{aligned}\]
が成り立つ ($0 < x < 2$ に注意).
この円錐の頂点 $\mathrm A$ から底面に下ろした垂線 $\mathrm{AH}$ は球の中心 $\mathrm O$ を通り,
$\mathrm{AB}$ を円錐の母線とすると $\triangle\mathrm{OBH}$ は $\angle\mathrm H = 90^\circ$ なる直角三角形になるから,
\[\begin{aligned}
r^2 &= \mathrm{BH}^2 = \mathrm{OB}^2-\mathrm{OH}^2 \\
&= 1^2-(x-1)^2 = 2x-x^2
\end{aligned}\]
が成り立つ.
よって,
\[ V = \frac{1}{3}\cdot\pi r^2\cdot x = \frac{\pi}{3}(2x^2-x^3)\]
であるから,
\[\frac{dV}{dx} = \frac{\pi}{3}(4x-3x^2) = -\frac{\pi}{3}x(3x-4)\]
であり,
\[\begin{aligned}
\frac{dV}{dx} \geqq 0 &\iff 0 < x \leqq \frac{4}{3}, \\
\frac{dV}{dx} \leqq 0 &\iff \frac{4}{3} \leqq x < 2
\end{aligned}\]
が成り立つ ($0 < x < 2$ に注意).
よって, $V$ は $x = \dfrac{4}{3},$ $r = \sqrt{\dfrac{4}{3}\left( 2-\dfrac{4}{3}\right)} = \dfrac{2\sqrt 2}{3}$ のとき極大かつ最大の値
\[\frac{\pi}{3}\left(\frac{4}{3}\right) ^2\left( 2-\frac{4}{3}\right) = \frac{32}{81}\pi\]
をとる.

| $x$ | $0$ | $\cdots$ | $\dfrac{4}{3}$ | $\cdots$ | $2$ |
| $\dfrac{dV}{dx}$ | $+$ | $0$ | $-$ | ||
| $V$ | $\nearrow$ | 極大 | $\searrow$ |
問題《表面積が一定である円柱の体積の最大値》
$S$ を正の数とする.
- (A)
- 表面積が $S$ である直円柱の体積 $V$ が最大になるとき, 底面の半径 $x$ と高さ $h$ の比, $V$ の値を求めよ.
- (B)
- 側面積と底面積の和が $S$ である, ふたのない, 薄い直円柱の形をした容器の容積 $V$ が最大になるとき, 底面の半径 $x$ と高さ $h$ の比, $V$ の値を求めよ. ただし, 側面積と底面積は, いずれも容器の外側のみを測るものとする.
解答例
- (A)
- $S = 2\pi x^2+2\pi xh$ であるから,
\[ h = \frac{S}{2\pi x}-x\]
が成り立つ.
よって,
\[ V = \pi x^2h = \pi x^2\left(\frac{S}{2\pi x}-x\right) = \frac{S}{2}x-\pi x^3\]
であるから
\[\frac{dV}{dx} = \frac{S}{2}-3\pi x^2\]
であり,
\[\begin{aligned}
\frac{dV}{dx} \geqq 0 &\iff 0 < x \leqq \sqrt{\frac{S}{6\pi}}, \\
\frac{dV}{dx} \leqq 0 &\iff \sqrt{\frac{S}{6\pi}} \leqq x < \sqrt{\frac{S}{2\pi}}
\end{aligned}\]
が成り立つ ($0 < x < \sqrt{\dfrac{S}{2\pi}}$ に注意).
よって, $x = \sqrt{\dfrac{S}{6\pi}}$ のとき, $V$ は極大かつ最大の値をとる. このとき, \[ h = S\div 2\pi\sqrt{\frac{S}{6\pi}}-\sqrt{\frac{S}{6\pi}} = 3\sqrt{\frac{S}{6\pi}}-\sqrt{\frac{S}{6\pi}} = 2\sqrt{\frac{S}{6\pi}}\] から $x:h = 1:2$ であり, \[ V = \pi x^2\cdot 2x = 2\pi x^3 = 2\pi\left(\sqrt{\frac{S}{6\pi}}\right) ^3 = \frac{S}{3}\sqrt{\frac{S}{6\pi}}\] である.
$x$ $0$ $\cdots$ $\sqrt{\dfrac{S}{6\pi}}$ $\cdots$ $\sqrt{\dfrac{S}{2\pi}}$ $\dfrac{dV}{dx}$ $+$ $0$ $-$ $V$ $\nearrow$ 極大 $\searrow$ - (B)
- $S = \pi x^2+2\pi xh$ であるから,
\[ h = \frac{S}{2\pi x}-\frac{x}{2}\]
が成り立つ.
よって,
\[ V = \pi x^2h = \pi x^2\left(\frac{S}{2\pi x}-\frac{x}{2}\right) = \frac{S}{2}x-\frac{\pi}{2}x^3\]
であるから
\[\frac{dV}{dx} = \frac{S}{2}-\frac{3\pi}{2}x^2\]
であり, $0 < x < \sqrt{\dfrac{S}{\pi}}$ に注意すると,
\[\begin{aligned}
\frac{dV}{dx} \geqq 0 &\iff 0 < x \leqq \sqrt{\frac{S}{3\pi}}, \\
\frac{dV}{dx} \leqq 0 &\iff \sqrt{\frac{S}{3\pi}} \leqq x < \sqrt{\frac{S}{\pi}}
\end{aligned}\]
が成り立つ.
よって, $x = \sqrt{\dfrac{S}{3\pi}}$ のとき, $V$ は極大かつ最大の値をとる. このとき, \[ h = S\!\div\!2\pi\sqrt{\frac{S}{3\pi}}\!-\!\frac{1}{2}\sqrt{\frac{S}{3\pi}} = \frac{3}{2}\sqrt{\frac{S}{3\pi}}\!-\!\frac{1}{2}\sqrt{\frac{S}{3\pi}} = \sqrt{\frac{S}{3\pi}}\] から $x:h = 1:1$ であり, \[ V = \pi x^2\cdot x = \pi x^3 = \pi\left(\sqrt{\frac{S}{3\pi}}\right) ^3 = \frac{S}{3}\sqrt{\frac{S}{3\pi}}\] である.
$x$ $0$ $\cdots$ $\sqrt{\dfrac{S}{3\pi}}$ $\cdots$ $\sqrt{\dfrac{S}{\pi}}$ $\dfrac{dV}{dx}$ $+$ $0$ $-$ $V$ $\nearrow$ 極大 $\searrow$
問題《円錐形の容器の容積の最大値》
半径 $1$ の扇形の直線部分を貼り合わせて, ふたのない, 薄い円錐形の容器を作る.
容器の容積 $V$ が最大になるようにするとき, 扇形の中心角の大きさ $\theta,$ $V$ の値を求めよ.
解答例
円錐の底面の半径を $x$ とおく.
このとき, 容器の高さ $h$ は三平方の定理により
\[ h = \sqrt{1-x^2}\]
であるから, 容器の容積は
\[ V = \frac{1}{3}\pi x^2h = \frac{1}{3}\pi x^2\sqrt{1-x^2}\]
である.
$f(x) = (x^2\sqrt{1-x^2})^2$ とおく.
\[ f(x) = x^4(1-x^2) = x^4-x^6\]
であるから
\[ f'(x) = 4x^3-6x^5 = -6x^3\left( x^2-\frac{2}{3}\right)\]
であり,
\[\begin{aligned}
f'(x) \geqq 0 &\iff 0 < x \leqq \sqrt{\frac{2}{3}}, \\
f'(x) \leqq 0 &\iff \sqrt{\frac{2}{3}} \leqq x < 1
\end{aligned}\]
が成り立つ ($0 < x < 1$ に注意).
よって, $x = \sqrt{\dfrac{2}{3}}$ のとき, $f(x)$ は極大かつ最大の値をとる.
このとき, $V$ は最大であり,
\[\begin{aligned}
\theta &= 2\pi x = 2\pi\sqrt{\dfrac{2}{3}}, \\
V &= \frac{1}{3}\pi\left(\sqrt{\frac{2}{3}}\right) ^2\sqrt{1-\left(\sqrt{\frac{2}{3}}\right) ^2} = \frac{2\pi}{9\sqrt 3}
\end{aligned}\]
である.
| $x$ | $0$ | $\cdots$ | $\sqrt{\dfrac{2}{3}}$ | $\cdots$ | $1$ | |
| $f'(x)$ | $+$ | $0$ | $-$ | |||
| $f(x)$ | $\nearrow$ | 極大 | $\searrow$ |
問題《三角形の等周問題》
周の長さが $1$ の三角形のうち面積が最大のものは正三角形であることを示せ.
解答例
$x$ を $0 < x < 1$ なる実数とする.
周の長さが $1,$ 底辺の長さが $x$ の三角形のうち面積が最大になるのは, 高さが最大になる, 二等辺三角形である.
このような三角形について, 等辺の長さは $\dfrac{1-x}{2}$ であるから, 面積を $S(x)$ とおくと,
\[ S(x) = \frac{1}{2}x\sqrt{\left(\frac{1-x}{2}\right)^2-\left(\frac{x}{2}\right) ^2} = \frac{1}{4}x\sqrt{1-2x}\]
となり,
\[ 16S(x)^2 = x^2(1-2x)\]
となる.
右辺を $x$ の関数として, $f(x)$ とおく.
このとき, $f(x) = x^2-2x^3$ から
\[ f'(x) = 2x-6x^2 = 2x(1-3x),\]
であるので,
\[\begin{aligned}
f'(x) \geqq 0 &\iff 0 < x \leqq \frac{1}{3}, \\
f'(x) \leqq 0 &\iff \frac{1}{3} \leqq x < 1
\end{aligned}\]
が成り立つ.
よって, $f(x)$ は $x = \dfrac{1}{3}$ のとき極大かつ最大の値をとる.
したがって, $S(x)$ は $x = \dfrac{1}{3}$ のとき最大値をとる.
ゆえに, 周の長さが $1$ の三角形のうち面積が最大のものは正三角形である.
別解
こちらを参照.
参考
- 周の長さが一定の図形のうち面積が最大の図形を求める問題を「等周問題」(isoperimetric problem) と呼ぶ.
- 四角形の「等周問題」は, 次のように三角形の場合よりも簡単に解ける: 四角形 $\mathrm{ABCD}$ の周の長さを変えずに頂点を動かすとき, 辺 $\mathrm{CD}$ と $\mathrm{DA}$ を固定した状態で面積が最大になるのは $\triangle\mathrm{ABC}$ の辺 $\mathrm{AC}$ に対する高さが最大になる $\mathrm{AB} = \mathrm{BC}$ の場合であり, 同様に辺 $\mathrm{AB}$ と $\mathrm{BC}$ を固定した状態で面積が最大になるのは $\mathrm{CD} = \mathrm{DA}$ の場合である. さらに, 辺 $\mathrm{BC}$ と $\mathrm{CD}$ を固定した状態で面積が最大になるのは $\mathrm{DA} = \mathrm{AB}$ の場合, 辺 $\mathrm{DA}$ と $\mathrm{AB}$ を固定した状態で面積が最大になるのは $\mathrm{BC} = \mathrm{CD}$ の場合である. よって, 四角形 $\mathrm{ABCD}$ の面積が最大になるのは $\mathrm{AB} = \mathrm{BC} = \mathrm{CD} = \mathrm{DA}$ の場合である. つまり, 周の長さが一定の四角形のうち面積が最大のものは正方形である.
