複素数平面上の変換
複素数平面上の変換
問題《反転と円円対応》
$\alpha$ を $0$ でない複素数とする.
- (1)
- $2$ 点 $\mathrm O(0),$ $\mathrm A(\alpha )$ を結ぶ線分の垂直二等分線は $\dfrac{z}{\alpha}+\dfrac{\bar z}{\bar \alpha} = 1$ で表されることを示せ.
- (2)
- 複素数平面上の原点 $\mathrm O$ と異なる点 $\mathrm P(z)$ と半直線 $\mathrm{OP}$ 上の点 $\mathrm Q(w)$ が $\mathrm{OP}\cdot\mathrm{OQ} = 1$ を満たすとする.
- ①
- $w$ を用いて $z$ を表せ.
- ②
- 点 $\mathrm P$ が円周 $|z-\alpha | = r$ 上を動くとする. 点 $\mathrm Q$ は, $|\alpha | = r$ のとき原点を通らない直線を描き, $|\alpha| \neq r$ のとき原点を通らない円周を描くことを示せ.
(参考: $2016$ 北海道大)
解答例
- (1)
- 複素数平面上の点 $\mathrm P(z)$ に対して
であるから, 線分 $\mathrm{OA}$ の垂直二等分線は方程式 $\dfrac{z}{\alpha}+\dfrac{\bar z}{\bar \alpha} = 1$ で表される.
点 $\mathrm P$ が線分 $\mathrm{OA}$ の垂直二等分線上にある $\iff$ $\mathrm{OP} = \mathrm{AP}$ $\iff$ $|z| = |z-\alpha |$ $\iff$ $|z|^2 = | z-\alpha |^2$ $\iff$ $z\bar z = (z-\alpha )\overline{(z-\alpha )}$ $\iff$ $z\bar z = (z-\alpha )(\bar z-\bar\alpha )$ $\iff$ $z\bar z = z\bar z-\bar\alpha z-\alpha\bar z+\alpha\bar\alpha$ $\iff$ $\bar\alpha z+\alpha\bar z = \alpha\bar\alpha$ $\iff$ $\dfrac{z}{\alpha}+\dfrac{\bar z}{\bar\alpha} = 1$ - (2)
- ①
- 点 $\mathrm Q$ は半直線 $\mathrm{OP}$ 上にあるから, $0$ 以上のある実数 $k$ に対して $z = kw$ となる. $\mathrm{OP}\cdot\mathrm{OQ} = 1$ から \[ 1 = |z||w| = |kw||w| = k|w|^2\] であるので, $k = \dfrac{1}{|w|^2}$ が成り立つ. よって, \[ z = \frac{1}{|w|^2}w = \frac{w}{w\bar w} = \frac{1}{\bar w} \quad \cdots [\text A]\] が成り立つ.
- ②
- $|z-\alpha | = r$ に $[\text A]$ を代入すると
\[\left|\frac{1}{\bar w}-\alpha\right| = r\]
となるから,
\[\begin{aligned}
r^2 &= \left|\frac{1}{\bar w}-\alpha\right| ^2 = \left(\frac{1}{\bar w}-\alpha\right)\overline{\left(\frac{1}{\bar w}-\alpha\right)} \\
&= \left(\frac{1}{\bar w}-\alpha\right)\left(\frac{1}{w}-\bar\alpha\right) \\
&= \frac{1}{\bar ww}-\frac{\bar\alpha}{\bar w}-\frac{\alpha}{w}+|\alpha |^2
\end{aligned}\]
となる.
両辺に $w\bar w$ を掛けて整理すると,
\[ (|\alpha |^2-r^2)w\bar w-\bar\alpha w-\alpha\bar w+1 = 0 \quad \cdots [\text B]\]
となる.
- (i)
- $|\alpha | = r$ の場合. \[ [\text B] \iff \bar\alpha w+\alpha\bar w = 1\] となるから, (1) の結果により, 点 $\mathrm Q$ の軌跡は $2$ 点 $0,$ $\bar\alpha ^{-1}$ を結ぶ線分の垂直二等分線である. よって, 点 $\mathrm Q$ は原点を通らない直線を描く.
- (ii)
- $|\alpha | \neq r$ の場合. $d = |\alpha |^2-r^2$ とおくと \[\begin{aligned} [\text B] &\iff w\bar w-\frac{\bar\alpha}{d}w-\frac{\alpha}{d}\bar w+\frac{\alpha\bar\alpha}{d^2} = \frac{|\alpha |^2}{d^2}-\frac{1}{d} \\ &\iff \left( w-\frac{\alpha}{d}\right)\left(\bar w-\frac{\bar\alpha}{d}\right) = \frac{r^2}{d^2} \\ &\iff \left( w-\frac{\alpha}{d}\right)\overline{\left( w-\frac{\alpha}{d}\right)} = \frac{r^2}{d^2} \\ &\iff \left| w-\frac{\alpha}{d}\right| ^2 = \frac{r^2}{d^2} \\ &\iff \left| w-\frac{\alpha}{d}\right| = \frac{r}{|d|} \end{aligned}\] となるから, 点 $\mathrm Q$ の軌跡は点 $\dfrac{\alpha}{|\alpha |^2-r^2}$ を中心とする半径 $\dfrac{r}{||\alpha |^2-r^2|}$ の円周である. よって, 点 $\mathrm Q$ は原点を通らない円周を描く.
参考
- 集合 $S$ の各要素に $S$ の $1$ つの要素を対応させる規則を $S$ 上の「変換」と呼ぶ. 例えば, 実数全体 $\mathbb R$ を定義域とする実数値関数は $\mathbb R$ 上の「変換」である. また, 複素数平面における平行移動, 回転移動, 対称移動はすべて複素数平面上の「変換」である. さらに, 複素数平面上の各点を定点からの距離がもとの定数倍になるような点にうつす対応も「相似変換」または「拡大・縮小変換」と呼ばれる「変換」である.
- 平面上の点 $\mathrm O$ を中心とする半径 $r$ の円周 $C$ について, $\mathrm O$ と異なる点 $\mathrm P$ を $\mathrm{OP}\cdot\mathrm{OQ} = r^2$ なる半直線 $\mathrm{OP}$ 上の点 $\mathrm Q$ に対応させる「変換」を円周 $C$ に関する「反転」と呼び, 点 $\mathrm O$ を「反転の中心」, $r$ を「反転の半径」と呼ぶ. また, 点 $\mathrm P$ が図形 $F$ 上を動くとき, 点 $\mathrm Q$ の軌跡を $F$ の「反形」と呼ぶ.
- 複素数平面 (原点を除く部分) において,「反転」$w = \dfrac{1}{\bar z}$ は, 実軸に関する対称移動と「変換」$w = \dfrac{1}{z}$ の「合成変換」である. 前者の「変換」が円周を円周にうつし, 後者の「変換」が円周を円周または直線にうつすことから,「反転」$w = \dfrac{1}{\bar z}$ は円周を円周または直線にうつす.
問題《$1$ 次分数変換と円円対応》
$\alpha \neq 0,$ $|\alpha | < 1,$ $|\lambda | = 1$ なる複素数 $\alpha,$ $\lambda$ に対して, $w = \lambda\dfrac{z-\alpha}{\bar\alpha z-1}$ は単位円 $|z| \leqq 1$ を単位円 $|w| \leqq 1$ にうつすことを示せ.
解答例
$w = \lambda\dfrac{z-\alpha}{\bar\alpha z-1}\ \cdots [1]$ とおく.
このとき, $(\bar\alpha z-1)w = \lambda (z-\alpha )$ から, $(\bar\alpha w-\lambda )z = w-\alpha\lambda$ となる.
ここで, 仮に $\bar\alpha w-\lambda = 0$ とすると, $w = \dfrac{\lambda}{\bar\alpha}$ から $0 = \dfrac{\lambda}{\bar\alpha}-\alpha\lambda = \dfrac{\lambda}{\bar\alpha}(1-|\alpha |^2)$ となり, $|\alpha |^2 = 1$ つまり $|\alpha | = 1$ となってしまう.
よって, $\bar\alpha w-\lambda \neq 0$ であり, $z = \dfrac{w-\alpha\lambda}{\bar\alpha w-\lambda}$ であるから, \[\begin{aligned} &|z| \leqq 1 \iff |z|^2 \leqq 1 \\ &\iff \left|\frac{w-\alpha\lambda}{\bar\alpha w-\lambda}\right| ^2 \leqq 1 \\ &\iff |w-\alpha\lambda |^2 \leqq |\bar\alpha w-\lambda |^2 \\ &\iff (w-\alpha\lambda )(\bar w-\bar\alpha\bar\lambda ) \leqq (\bar\alpha w-\lambda )(\alpha\bar w-\bar\lambda ) \\ &\iff |w|^2-\bar\alpha\bar\lambda w-\alpha\lambda\bar w+|\alpha |^2 \\ &\qquad\quad \leqq |\alpha |^2|w|^2-\bar\alpha\bar\lambda w-\alpha\lambda\bar w+1 \quad (\because |\lambda | = 1) \\ &\iff (1-|\alpha |^2)|w|^2 \leqq 1-|\alpha |^2 \\ &\iff |w|^2 \leqq 1 \quad (\because |\alpha | < 1) \\ &\iff |w| \leqq 1 \end{aligned}\] が成り立つ. ゆえに, $[1]$ は単位円 $|z| \leqq 1$ を単位円 $|w| \leqq 1$ にうつす.
ここで, 仮に $\bar\alpha w-\lambda = 0$ とすると, $w = \dfrac{\lambda}{\bar\alpha}$ から $0 = \dfrac{\lambda}{\bar\alpha}-\alpha\lambda = \dfrac{\lambda}{\bar\alpha}(1-|\alpha |^2)$ となり, $|\alpha |^2 = 1$ つまり $|\alpha | = 1$ となってしまう.
よって, $\bar\alpha w-\lambda \neq 0$ であり, $z = \dfrac{w-\alpha\lambda}{\bar\alpha w-\lambda}$ であるから, \[\begin{aligned} &|z| \leqq 1 \iff |z|^2 \leqq 1 \\ &\iff \left|\frac{w-\alpha\lambda}{\bar\alpha w-\lambda}\right| ^2 \leqq 1 \\ &\iff |w-\alpha\lambda |^2 \leqq |\bar\alpha w-\lambda |^2 \\ &\iff (w-\alpha\lambda )(\bar w-\bar\alpha\bar\lambda ) \leqq (\bar\alpha w-\lambda )(\alpha\bar w-\bar\lambda ) \\ &\iff |w|^2-\bar\alpha\bar\lambda w-\alpha\lambda\bar w+|\alpha |^2 \\ &\qquad\quad \leqq |\alpha |^2|w|^2-\bar\alpha\bar\lambda w-\alpha\lambda\bar w+1 \quad (\because |\lambda | = 1) \\ &\iff (1-|\alpha |^2)|w|^2 \leqq 1-|\alpha |^2 \\ &\iff |w|^2 \leqq 1 \quad (\because |\alpha | < 1) \\ &\iff |w| \leqq 1 \end{aligned}\] が成り立つ. ゆえに, $[1]$ は単位円 $|z| \leqq 1$ を単位円 $|w| \leqq 1$ にうつす.
参考
- $\alpha\delta -\beta\gamma \neq 0,$ $(\gamma,\delta ) \neq (0,0)$ なる複素数 $\alpha,$ $\beta,$ $\gamma,$ $\delta$ を用いて \[ w = \dfrac{\alpha z+\beta}{\gamma z+\delta} \quad \cdots [*]\] の形に表される変換は「$1$ 次分数変換」または「メビウス変換」と呼ばれる.
- (i)
- $\gamma \neq 0$ のとき, $[*]$ は, \[ w = \frac{\alpha}{\gamma}+\frac{\dfrac{\beta\gamma -\alpha\delta}{\gamma ^2}}{z+\dfrac{\delta}{\gamma}}\] と変形でき, 平行移動,「反転」, 回転移動と相似変換, 平行移動の合成と一致する.
- (ii)
- $\gamma = 0$ のとき, $[*]$ は, \[ w = \frac{\alpha}{\delta}\left( z+\frac{\beta}{\alpha}\right)\] と変形でき, 平行移動, 回転移動と相似変換の合成と一致する.
問題《ケイリー変換》
複素数平面上の点 $z$ が実軸の上方 (実軸上の点は含まない) を動くとき, 点 $w = \dfrac{z-i}{z+i}$ が動く範囲を求めよ.
解答例
実軸は $2$ 点 $i,$ $-i$ を結ぶ線分の垂直二等分線 $|z-i| = |z+i|$ と一致する.
よって, $w = \dfrac{z-i}{z+i}$ であるとき,
が成り立つから, 複素数平面上の点 $z$ が実軸の上方を動くとき, 点 $w$ が動く範囲は単位円の内部 (周上の点は含まない) である.
| 点 $z$ が実軸の上方 | $\iff$ $|z-i| < |z+i|$ |
| $\iff$ $\left|\dfrac{z-i}{z+i}\right| < 1$ | |
| $\iff$ $|w| < 1$ |
参考
「変換」$f(z) = \dfrac{z-i}{z+i}$ は「ケイリー変換」(Cayley transformation) と呼ばれ,「複素解析学」で重要な役割を果たす.
問題《複比の $1$ 次変換による不変性とその応用》
相異なる複素数 $z_1,$ $z_2,$ $z_3,$ $z_4$ に対して, 比
\[\frac{(z_3-z_1)(z_4-z_2)}{(z_3-z_2)(z_4-z_1)}\]
を $(z_1,z_2;z_3,z_4)$ で表す.
次のことを示せ.
- (1)
- $f(z) = k(z-\alpha )$ ($k$: $0$ でない実数, $\alpha$: 複素数) のとき, \[ (f(z_1),f(z_2);f(z_3),f(z_4)) = (z_1,z_2;z_3,z_4)\] が成り立つ.
- (2)
- 複素数平面において, 点 $z_1,$ $z_2,$ $z_3$ が単位円周上にあるとする. このとき, 点 $z_4$ が単位円周上にあることと $(z_1,z_2;z_3,z_4)$ が実数であることは同値である.
- (3)
- 複素数平面において, 点 $z_1,$ $z_2,$ $z_3$ が円周 $C$ 上にあるとする. このとき, 点 $z_4$ が円周 $C$ 上にあることと $(z_1,z_2;z_3,z_4)$ が実数であることは同値である.
(参考: $1999$ 京都大)
解答例
- (1)
- $f(z) = k(z-\alpha )$ のとき, \[\begin{aligned} &(f(z_1),f(z_2);f(z_3),f(z_4)) \\ &= \frac{\{ f(z_3)-f(z_1)\}\{ f(z_4)-f(z_2)\}}{\{ f(z_3)-f(z_2)\}\{ f(z_4)-f(z_1)\}} \\ &= \frac{\{ k(z_3-\alpha )-k(z_1-\alpha )\}\{ k(z_4-\alpha )-k(z_2-\alpha )\}}{\{ k(z_3-\alpha )-k(z_2-\alpha )\}\{ k(z_4-\alpha )-k(z_1-\alpha )\}} \\ &= \frac{k^2(z_3-z_1)(z_4-z_2)}{k^2(z_3-z_2)(z_4-z_1)} = \frac{(z_3-z_1)(z_4-z_2)}{(z_3-z_2)(z_4-z_1)} \\ &= (z_1,z_2;z_3,z_4) \end{aligned}\] が成り立つ.
- (2)
- 点 $z_1,$ $z_2,$ $z_3$ が単位円周上にあるとする.
このとき, 各番号 $k$ $(1 \leqq k \leqq 3)$ に対して, $z_k\overline{z_k} = |z_k|^2 = 1$ から,
\[\overline{z_k} = z_k{}^{-1} \quad \cdots [1]\]
が成り立つ.
- (i)
- 点 $z_4$ が単位円周上にあるとする. このとき, $k = 4$ に対しても $[1]$ が成り立つ. よって, \[\begin{aligned} \overline{(z_1,z_2;z_3,z_4)} &= \overline{\ \frac{(z_3-z_1)(z_4-z_2)}{(z_3-z_2)(z_4-z_1)}\ } \\ &= \frac{(\overline{z_3}-\overline{z_1})(\overline{z_4}-\overline{z_2})}{(\overline{z_3}-\overline{z_2})(\overline{z_4}-\overline{z_1})} \\ &= \frac{(z_3{}^{-1}-z_1{}^{-1})(z_4{}^{-1}-z_2{}^{-1})}{(z_3{}^{-1}-z_2{}^{-1})(z_4{}^{-1}-z_1{}^{-1})} \\ &= \frac{(z_1-z_3)(z_2-z_4)}{(z_2-z_3)(z_1-z_4)} \\ &= \frac{(z_3-z_1)(z_4-z_2)}{(z_3-z_2)(z_4-z_1)} \\ &= (z_1,z_2;z_3,z_4) \end{aligned}\] が成り立つから, $(z_1,z_2;z_3,z_4)$ は実数である.
- (ii)
- $(z_1,z_2;z_3,z_4)$ が実数であるとする. このとき, $(z_1,z_2;z_3,z_4) = \overline{(z_1,z_2;z_3,z_4)}$ から, \[\begin{aligned} \frac{(z_3-z_1)(z_4-z_2)}{(z_3-z_2)(z_4-z_1)} &= \overline{\ \frac{(z_3-z_1)(z_4-z_2)}{(z_3-z_2)(z_4-z_1)}\ } \\ &= \frac{(\overline{z_3}-\overline{z_1})(\overline{z_4}-\overline{z_2})}{(\overline{z_3}-\overline{z_2})(\overline{z_4}-\overline{z_1})} \\ &= \frac{(z_3{}^{-1}-z_1{}^{-1})(\overline{z_4}-z_2{}^{-1})}{(z_3{}^{-1}-z_2{}^{-1})(\overline{z_4}-z_1{}^{-1})} \\ &= \frac{(z_1-z_3)(z_2\overline{z_4}-1)}{(z_2-z_3)(z_1\overline{z_4}-1)} \end{aligned}\] よって \[\begin{aligned} \frac{z_4-z_2}{z_4-z_1} &= \frac{z_2\overline{z_4}-1}{z_1\overline{z_4}-1} \\ (z_4-z_2)(z_1\overline{z_4}-1) &= (z_4-z_1)(z_2\overline{z_4}-1) \end{aligned}\] が成り立つ. 展開して整理すると \[ (z_1-z_2)(|z_4|^2-1) = 0\] となるから, $|z_4|^2 = 1$ つまり $|z_4| = 1$ が成り立つ. これは点 $z_4$ が単位円周上にあることを意味する.
- (3)
- $C$ が点 $\alpha$ を中心とする半径 $r$ の円周であるとし,
\[ f(z) = \dfrac{1}{r}(z-\alpha )\]
とおく.
このとき, 点 $z$ が $C$ 上にあることと, 点 $f(z)$ が単位円周 $C_0$ 上にあることは同値である.
また, (1) により
\[ (f(z_1),f(z_2);f(z_3),f(z_4)) = (z_1,z_2;z_3,z_4)\]
であるから,
が成り立つ.
$z_4 \in C$ $\iff$ $f(z_4) \in C_0$ $\iff$ $(f(z_1),f(z_2);f(z_3),f(z_4))$ は実数 $(\because (2))$ $\iff$ $(z_1,z_2;z_3,z_4)$ は実数
参考
- 複素数平面上の相異なる $4$ 点 $z_1,$ $z_2,$ $z_3,$ $z_4$ に対して, 比 \[\frac{(z_3-z_1)(z_4-z_2)}{(z_3-z_2)(z_4-z_1)}\] を「複比」または「非調和比」(cross ratio) と呼び, $(z_1,z_2;z_3,z_4)$ で表す. 「複比」の概念は「射影幾何学」で重要な役割を果たす.
- 「複比」は, 平行移動, 回転移動や相似変換, 変換 $f(z) = \dfrac{1}{z}$ に関して不変である (各自確認されたい). 「$1$ 次分数変換」はそれらの合成であるから (こちらを参照),「複比」は「$1$ 次分数変換」に関して不変である. (2) は「複比」が変換 $f(z) = \dfrac{1}{z}$ に関して不変であることの帰結である.
問題《ジューコフスキー変換》
$a,$ $r$ を正の数とする.
点 $z$ が原点を中心とする半径 $r$ の円周上を動くとき, $w = z+\dfrac{a^2}{z}$ を満たす点 $w$ の軌跡を,
(i) $a = r$ のとき (ii) $a \neq r$ のとき
の $2$ つの場合に分けて求めよ.
解答例
$z = r(\cos\theta +i\sin\theta )$ $(r > 0,\ 0 \leqq \theta < 2\pi )$ とおく.
このとき,
\[\begin{aligned}
w &= z+\frac{a^2}{z} = r(\cos\theta +i\sin\theta )+\frac{a^2}{r}(\cos\theta -i\sin\theta ) \\
&= \left( r+\frac{a^2}{r}\right)\cos\theta +i\left( r-\frac{a^2}{r}\right)\sin\theta \\
&= \frac{r^2+a^2}{r}\cos\theta +i\frac{r^2-a^2}{r}\sin\theta \quad \cdots [1]
\end{aligned}\]
となる.
- (i)
- $a = r$ のとき. \[ [1] \iff w = 2a\cos\theta\] から $w$ は実数であり, $-1 \leqq \cos\theta \leqq 1$ から $-2a \leqq w \leqq 2a$ であるので, 点 $w$ は $2$ 点 $-2a,$ $2a$ を結ぶ線分を描く.
- (ii)
- $a \neq r$ のとき.
$w = x+yi$ ($x,$ $y$: 実数) とおく.
このとき, $[1]$ から
\[ x = \frac{r^2+a^2}{r}\cos\theta, \quad y = \frac{r^2-a^2}{r}\sin\theta\]
となる.
$\cos ^2\theta +\sin ^2\theta = 1$ を使って $\theta$ を消去すると,
\[ [1] \iff \frac{x^2}{\left(\dfrac{r^2+a^2}{r}\right) ^2}+\frac{y^2}{\left(\dfrac{r^2-a^2}{r}\right) ^2} = 1\]
となる.
よって, 点 $w$ は
を焦点とする長軸の長さ $\dfrac{2(r^2+a^2)}{r},$ 短軸の長さ $\dfrac{2|r^2-a^2|}{r}$ の楕円の周を描く.
$\left(\pm\sqrt{\left(\dfrac{r^2+a^2}{r}\right) ^2-\left(\dfrac{r^2-a^2}{r}\right) ^2},0\right)$ つまり $(\pm 2a,0)$
参考
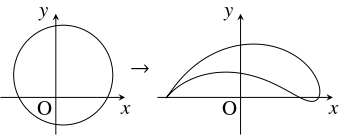
$w = z+\dfrac{a^2}{z}$ ($a$: 正の定数) の形の関係式によって $z$ を $w$ に対応させる複素数平面上の「変換」を「ジューコフスキー変換」(Joukowski transformation, Zhukovsky —) と呼ぶ.
この「変換」は流体力学において翼の揚力に関する理論に応用されており, 飛行機の翼の設計に役立てられている.
例えば, 中心が原点から少し離れた円周は「ジューコフスキー変換」$w = z+\dfrac{1}{z}$ によって, 図のような曲線に「変換」される.