ガウス記号
ガウス記号
定義《ガウス記号》
各実数 $a$ に対して, $a$ 以下の最大の整数を $[a]$ で表す.
この記号 $[\ ]$ をガウス記号と呼ぶ.
ただし, この記法と呼称が通用するのは, 日本やドイツなど一部の地域に限られる.
英語圏では, これを $\lfloor a\rfloor$ で表して, 関数 $\lfloor\ \rfloor$ を floor function と呼ぶ.
定理《ガウス記号の性質》
すべての実数 $a$ に対して,
\[\begin{aligned}
&[a] \leqq a < [a]+1, \\
&a-1 < [a] \leqq a
\end{aligned}\]
が成り立つ.
問題《実数の四捨五入》
実数 $a$ を四捨五入した値は
\[\left[ a+\frac{1}{2}\right]\]
と表されることを示せ.
解答例
実数 $a$ を四捨五入した値を $k$ とおく.
- (i)
- $[a] \leqq a < [a]+\dfrac{1}{2}$ のとき.
$k = [a]$ であるから,
が成り立つ.$a < k+\dfrac{1}{2}$ つまり $a-\dfrac{1}{2} < k$ - (ii)
- $[a]+\dfrac{1}{2} \leqq a < [a]+1$ のとき.
$k = [a]+1$ であるから,
が成り立つ.$k-\dfrac{1}{2} \leqq a$ つまり $k \leqq a+\dfrac{1}{2}$
問題《エルミートの恒等式》
$a$ を実数, $n$ を正の整数とする.
- (1)
- \[ n[a]+m \leqq na < n[a]+m+1\] を満たす $0$ 以上 $n$ 未満の整数 $m$ が存在することを示せ.
- (2)
- \[\sum_{k = 0}^{n-1}\left[ a+\frac{k}{n}\right] = [na]\]
が成り立つことを示せ.
(参考: $2019$ 京都府立大, $2018$ 富山大)
解答例
- (1)
- $0 \leqq a-[a] < 1$ から $0 \leqq n(a-[a]) < n$ であるので, \[ m \leqq n(a-[a]) < m+1\] を満たす $0$ 以上 $n$ 未満の整数 $m$ が存在する. この $m$ に対して \[ n[a]+m \leqq na < n[a]+m+1 \quad \cdots [1]\] が成り立つ.
- (2)
- $[1]$ から, \[ [na] = n[a]+m \quad \cdots [2]\] が成り立つ. 一方, $0$ 以上 $n-1$ 以下の各整数 $k$ に対して, $[1]$ の辺々を $n$ で割って $\dfrac{k}{n}$ を加えると \[ [a]+\frac{m+k}{n} \leqq a+\frac{k}{n} < [a]+\frac{m+k+1}{n}\] となるので, \[\left[ a+\frac{k}{n}\right] = \begin{cases} [a] & (0 \leqq k \leqq n-m-1) \\ [a]+1 & (n-m \leqq k \leqq n-1) \end{cases}\] が成り立つ. よって, これらの和をとると, \[\begin{aligned} \sum_{k = 0}^{n-1}\left[ a+\frac{k}{n}\right] &= (n-m)[a]+m([a]+1) \\ &= n[a]+m \quad \cdots [3] \end{aligned}\] が得られる. ゆえに, $[2],$ $[3]$ から, \[\sum_{k = 0}^{n-1}\left[ a+\frac{k}{n}\right] = [na]\] が成り立つ.
参考
(2) の等式は「エルミートの恒等式」(Hermite's identity) として知られている.
問題《レイリー=ビーティの定理》
各実数 $a$ に対して, $a$ 以下の最大の整数を $[a]$ で表す.
$x,$ $y$ を $\dfrac{1}{x}+\dfrac{1}{y} = 1$ なる正の数とする.
- (A)
- 正の整数 $m,$ $n,$ $k$ に対して $[mx] = [ny] = k$ が成り立つとする.
このとき, 次のことを示せ.
- (1)
- $\dfrac{k}{x} \leqq m < \dfrac{k+1}{x}$ が成り立つ.
- (2)
- $m+n = k$ が成り立つ.
- (3)
- $x,$ $y$ は有理数である.
- (B)
- $x,$ $y$ が無理数であるとし, 実数 $k$ が $[mx],$ $[ny]$ ($m,$ $n$: 正の整数) の形に表されないとする. このとき, $k$ は整数でないことを示せ.
(参考: (A) $1992$ 慶應義塾大, (B) $2016$ 京都府立大)
解答例
- (A)
- (1)
- $[a] \leqq a < [a]+1$ に $a = mx$ を代入すると, $[mx] = k$ から \[ k \leqq mx < k+1\] となるので, \[\frac{k}{x} \leqq m < \frac{k+1}{x} \quad \cdots [1]\] が得られる.
- (2)
- (1) と同様にして, \[\frac{k}{y} \leqq n < \frac{k+1}{y} \quad \cdots [2]\] が得られる. $[1],$ $[2]$ の辺々を加えると, \[ k\left(\frac{1}{x}+\frac{1}{y}\right) \leqq m+n < (k+1)\left(\frac{1}{x}+\frac{1}{y}\right) \quad \cdots [3]\] となる. よって, $\dfrac{1}{x}+\dfrac{1}{y} = 1$ から, \[ k \leqq m+n < k+1 \quad \cdots [4]\] が成り立つ. $m,$ $n,$ $k$ は整数であるから, $m+n = k$ が成り立つ.
- (3)
- (2) から $[4]$ において等号が成り立つので, $[3]$ において等号が成り立つ.
よって, $[1],$ $[2]$ において等号が成り立つから,
$\dfrac{k}{x} = m,$ $\dfrac{k}{y} = n$ つまり $x = \dfrac{k}{m},$ $y = \dfrac{k}{n}$である. ゆえに, $x,$ $y$ は有理数である.
- (B)
- $x,$ $y$ は無理数であるから
\[\begin{aligned}
[mx] = p &\iff p < mx < p+1, \\
[ny] = q &\iff q < ny < q+1
\end{aligned}\]
であることに注意すると, 仮定から
\[\begin{aligned}
mx < k, \quad &k+1 < (m+1)x, \\
ny < k, \quad &k+1 < (n+1)y
\end{aligned}\]
を満たす正の整数 $m,$ $n$ の存在がわかる.
(例えば, $x = \dfrac{1+\sqrt 5}{2},$ $y = \dfrac{3+\sqrt 5}{2}$ のとき, $k = 3.5,$ $k+1 = 4.5$ は, ともに $2x = 3.2\cdots$ と $3x = 4.8\cdots$ の間, $y = 2.6\cdots$ と $2y = 5.2\cdots$ の間にある.)これらの不等式から \[\begin{aligned} &m+n < \frac{k}{x}+\frac{k}{y} = k, \\ &k+1 = \frac{k+1}{x}+\frac{k+1}{y} < (m+1)+(n+1) \end{aligned}\] が得られる. よって, \[ m+n < k < m+n+1\] が成り立つから, $k$ は整数でない.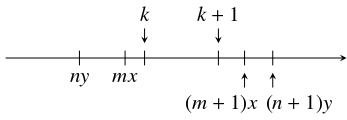
参考
- (A), (B) から,「レイリー=ビーティの定理」(Rayleigh–Beatty theorem) または「レイリーの定理」と呼ばれる, 次の定理が証明された: 与えられた正の数 $x,$ $y$ について, すべての正の整数が $[mx],$ $[ny]$ ($m,$ $n$: 正の整数) の形に重複なく表されるためには, $\dfrac{1}{x}+\dfrac{1}{y} = 1$ が成り立ち, $x,$ $y$ が無理数であることが必要十分である. 例えば,「黄金数」$\dfrac{1+\sqrt 5}{2}$ を $\varphi$ とおくとき, \[\frac{1}{\varphi}+\frac{1}{\varphi ^2} = \frac{2}{1+\sqrt 5}+\frac{2}{3+\sqrt 5} = \frac{\sqrt 5-1}{2}+\frac{3-\sqrt 5}{2} = 1\] であり, 正の整数全体の集合 $\mathbb Z_+$ は \[\begin{aligned} \{ [n\varphi ]|n \in \mathbb Z_+\} &= \{ 1,3,4,6,8,9,11,12,14,16,\cdots\}, \\ \{ [n\varphi ^2]|n \in \mathbb Z_+\} &= \{ 2,5,7,10,13,15,18,20,23,26,\cdots\} \end{aligned}\] という $2$ つの集合に「分割」される.
- $\dfrac{1}{x}+\dfrac{1}{y} = 1$ なる正の無理数 $x,$ $y$ に対して, 数列 $\{ [nx]\},$ $\{ [ny]\}$ を「ビーティ数列」(Beatty sequence) と呼ぶ. 「チャヌシッチ」または「ワイソフのゲーム」と呼ばれるゲーム (両方の山から同じ個数の石を取ることもできる $2$ 山崩し, 最後に石を取った方が勝ち) において, 後手必勝の局面は, 各山の石の個数の組合せが \[\{ [n\varphi ],[n\varphi ^2]\} \quad \left( n \in \mathbb Z_+,\ \varphi = \dfrac{1+\sqrt 5}{2}\right)\] の場合に限ることが知られている.
