空間図形の計量
空間図形の計量
問題《オイラーのレンガ》
横の長さが $44,$ 縦の長さが $117,$ 高さが $240$ の直方体において, 底面の対角線の長さ,「体対角線」(中心を通る対角線) の長さを求めよ.
解答例
底面の対角線の長さは
\[\sqrt{44^2+117^2} = \sqrt{15625} = 125\]
であるから,「体対角線」の長さは
\[\sqrt{125^2+240^2} = \sqrt{5^2(25^2+48^2)} = 5\sqrt{2929}\]
である.
参考
- 本問の直方体において, 残りの面の対角線の長さ \[\sqrt{117^2+240^2} = 267, \quad \sqrt{240^2+44^2} = 244\] も整数である. このように各辺と各面の対角線の長さが整数であるような直方体は「オイラーのレンガ」(Euler's brick) と呼ばれ, そのうち最小のものは本問の直方体であることが知られている. 無限に多くの「オイラーのレンガ」の辺の長さを与える公式が発見されているが, すべての「オイラーのレンガ」の辺の長さを表す公式はまだ発見されていない.
- 「オイラーのレンガ」のうち「体対角線」の長さも整数であるものは「完全直方体」(perfect cuboid) と呼ばれるが, その存在はまだ確認されていない.
問題《正多面体の外接球の半径》
$1$ 辺の長さが $1$ の正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体において, 最長対角線の長さ, 外接球の半径をそれぞれ求めよ.
ただし, $1$ 辺の長さが $1$ の正五角形の対角線の長さが「黄金数」
\[\varphi = \frac{1+\sqrt 5}{2}\]
であること (こちらとこちらを参照) は, 証明なしに使ってよい.
解答例
- 正四面体の対角線は存在しない. $1$ 辺の長さが $1$ の正四面体 $\mathrm{ABCD}$ の外接球の半径を $R$ とおく. また, 頂点 $\mathrm D$ から面 $\mathrm{ABC}$ に下ろした垂線の足を $\mathrm H$ とおく. 辺 $\mathrm{DH}$ を共有し, 斜辺の長さが等しい $3$ つの直角三角形 $\mathrm{ADH},$ $\mathrm{BDH},$ $\mathrm{CDH}$ は合同であるから, \[\mathrm{AH} = \mathrm{BH} = \mathrm{CH}\] である. よって, $\mathrm H$ は $\triangle\mathrm{ABC}$ の外心であるから, 正弦定理により \[\mathrm{AH} = \frac{1}{2\sin 60^\circ} = \frac{1}{\sqrt 3}\] である. 直角三角形 $\mathrm{ADH}$ に三平方の定理を適用すると, \[\mathrm{DH} = \sqrt{\mathrm{AD}^2-\mathrm{AH}^2} = \sqrt{1^2-\left(\frac{1}{\sqrt 3}\right) ^2} = \sqrt{\frac{2}{3}}\] が得られる. 垂線 $\mathrm{DH}$ は球の中心 $\mathrm O$ を通ることに注意して, 直角三角形 $\mathrm{AOH}$ に三平方の定理を適用すると, \[\left(\frac{1}{\sqrt 3}\right) ^2+\left(\sqrt{\frac{2}{3}}-R\right) ^2 = R^2, \quad 1-2\sqrt{\frac{2}{3}}R = 0\] よって \[ R = \frac{\sqrt 6}{4}\] が得られる.
- $1$ 辺の長さが $1$ の正六面体の最長対角線の長さ $d$ は \[ d = \sqrt{1^2+1^2+1^2} = \sqrt 3\] である. よって, 外接球の半径 $R$ は \[ R = \frac{d}{2} = \frac{\sqrt 3}{2}\] である.
- $1$ 辺の長さが $1$ の正八面体は $1$ 辺の長さが $2\cdot\dfrac{1}{\sqrt 2} = \sqrt 2$ の正六面体に内接するから, 最長対角線の長さ $d$ は \[ d = \sqrt 2\] である. よって, 外接球の半径 $R$ は \[ R = \frac{d}{2} = \frac{\sqrt 2}{2}\] である.
- $1$ 辺の長さが $1$ の正十二面体には $1$ 辺の長さが $\varphi = \dfrac{1+\sqrt 5}{2}$ の立方体 (頂点を $1$ つ飛ばしに結んで得られる) が内接するから, 最長対角線の長さ $d$ は \[ d = \sqrt{\varphi ^2+\varphi ^2+\varphi ^2} = \varphi\sqrt 3 = \frac{\sqrt 3+\sqrt{15}}{2}\] である. よって, 外接球の半径 $R$ は \[ R = \frac{d}{2} = \frac{\sqrt 3+\sqrt{15}}{4}\] である.
- $1$ 辺の長さが $1$ の正二十面体の最長対角線は隣り合う $2$ 辺の長さが $1,$ $\varphi = \dfrac{1+\sqrt 5}{2}$ の長方形の対角線と一致するから, 最長対角線の長さ $d$ は \[ d = \sqrt{1^2+\varphi ^2} = \sqrt{1+\frac{3+\sqrt 5}{2}} = \sqrt{\frac{5+\sqrt 5}{2}} = \frac{\sqrt{10+2\sqrt 5}}{2}\] である. よって, 外接球の半径 $R$ は \[ R = \frac{d}{2} = \frac{\sqrt{10+2\sqrt 5}}{4}\] である.
問題《正多面体の内接球の半径》
$1$ 辺の長さが $1$ の正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体において, 内接球の半径をそれぞれ求めよ.
ただし, 前問の結果は証明なしに使ってよい.
解答例
正多面体において, 中心 (外接球, 内接球の中心), 頂点 (外接球の接点), 面の中心 (内接球の接点) は直角三角形をなす.
- $1$ 辺の長さが $1$ の正四面体において, 外接球の半径 $R$ は \[ R = \frac{\sqrt 6}{4}\] で (前問参照), 頂点と面の中心の距離 $l$ は面の外接球の半径に等しく \[ l = \frac{1}{2\sin 60^\circ} = \frac{1}{\sqrt 3}\] であるから, 内接球の半径 $r$ は三平方の定理により \[\begin{aligned} r &= \sqrt{R^2-l^2} = \sqrt{\left(\frac{\sqrt 6}{4}\right) ^2-\left(\frac{1}{\sqrt 3}\right) ^2} \\ &= \sqrt{\frac{3}{8}-\frac{1}{3}} = \sqrt{\frac{1}{24}} = \frac{\sqrt 6}{12} \end{aligned}\] である.
- $1$ 辺の長さが $1$ の正六面体の内接球の半径 $r$ は \[ r = \frac{1}{2}\] である.
- $1$ 辺の長さが $1$ の正八面体において, 外接球の半径 $R$ は \[ R = \frac{\sqrt 2}{2}\] で (前問参照), 頂点と面の中心の距離 $l$ は面の外接球の半径に等しく \[ l = \frac{1}{2\sin 60^\circ} = \frac{1}{\sqrt 3}\] であるから, 内接球の半径 $r$ は三平方の定理により \[\begin{aligned} r &= \sqrt{R^2-l^2} = \sqrt{\left(\frac{\sqrt 2}{2}\right) ^2-\left(\frac{1}{\sqrt 3}\right) ^2} \\ &= \sqrt{\frac{1}{2}-\frac{1}{3}} = \sqrt{\frac{1}{6}} = \frac{\sqrt 6}{6} \end{aligned}\] である.
- $1$ 辺の長さが $1$ の正十二面体において, 外接球の半径 $R$ は \[ R = \frac{\sqrt 3+\sqrt{15}}{4}\] で (前問参照), 頂点と面の中心の距離 $l$ は面の外接球の半径に等しく \[ l = \frac{1}{2\sin 36^\circ} = \frac{2}{\sqrt{10-2\sqrt 5}}\] であるから, 内接球の半径 $r$ は三平方の定理により \[\begin{aligned} r &= \sqrt{R^2-l^2} = \sqrt{\left(\frac{\sqrt 3+\sqrt{15}}{4}\right) ^2-\left(\frac{2}{\sqrt{10-2\sqrt 5}}\right) ^2} \\ &= \sqrt{\frac{18+6\sqrt 5}{16}-\frac{4}{10-2\sqrt 5}} = \sqrt{\frac{9+3\sqrt 5}{8}-\frac{40+8\sqrt 5}{80}} \\ &= \sqrt{\frac{25+11\sqrt 5}{40}} = \frac{1}{2}\sqrt{\frac{25+11\sqrt 5}{10}} \end{aligned}\] である.
- $1$ 辺の長さが $1$ の正二十面体において, 外接球の半径 $R$ は \[ R = \frac{\sqrt{10+2\sqrt 5}}{4}\] で (前問参照), 頂点と面の中心の距離 $l$ は面の外接球の半径に等しく \[ l = \frac{1}{2\sin 60^\circ} = \frac{1}{\sqrt 3}\] であるから, 内接球の半径 $r$ は三平方の定理により \[\begin{aligned} r &= \sqrt{R^2-l^2} = \sqrt{\left(\frac{\sqrt{10+2\sqrt 5}}{4}\right) ^2-\left(\frac{1}{\sqrt 3}\right) ^2} \\ &= \sqrt{\frac{10+2\sqrt 5}{16}-\frac{1}{3}} = \sqrt{\frac{14+6\sqrt 5}{48}} = \sqrt{\frac{(3+\sqrt 5)^2}{48}} \\ &= \frac{3+\sqrt 5}{4\sqrt 3} = \frac{3\sqrt 3+\sqrt{15}}{12} \end{aligned}\] である.
別解
$1$ 辺の長さが $1$ の正四面体の体積は
\[\frac{\sqrt 2}{12}\cdot 1^3\]
である.
内接球の半径を $r$ とおき, 正四面体を内心を頂点とする $4$ つの正三角錐に分けると, この体積は
\[ 4\cdot\frac{1}{3}\left(\frac{1}{2}\cdot 1^2\cdot\frac{\sqrt 3}{2}\right) r = \frac{\sqrt 2}{12}\cdot 1^3\]
と表せるから,
\[ r = \frac{\sqrt 6}{12}\]
である.
問題《正多面体の表面積》
$1$ 辺の長さが $1$ の正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体において, 表面積をそれぞれ求めよ.
ただし,
\[\sin 36^\circ = \frac{\sqrt{10-2\sqrt 5}}{4}, \quad \sin 72^\circ = \frac{\sqrt{10+2\sqrt 5}}{4}\]
であることは, 証明なしに使ってよい.
解答例
$1$ 辺の長さが $1$ の正三角形, 正方形の面積は, それぞれ
\[\begin{aligned}
\frac{1}{2}\cdot 1^2\sin 60^\circ &= \frac{\sqrt 3}{4}, \\
1^2 &= 1
\end{aligned}\]
である.
また, $1$ 辺の長さが $1$ の正五角形は, 半径 $\dfrac{1}{2}\div\sin 36^\circ = \dfrac{1}{2\sin 36^\circ}$ の円に内接するから, その面積は
\[\begin{aligned}
&5\cdot\frac{1}{2}\cdot\left(\frac{1}{2\sin 36^\circ}\right) ^2\sin 72^\circ = \frac{5}{8}\cdot\frac{16}{10-2\sqrt 5}\cdot\frac{\sqrt{10+2\sqrt 5}}{4} \\
&= \frac{5}{4}\cdot\frac{\sqrt{10+2\sqrt 5}}{5-\sqrt 5} = \frac{5}{4}\cdot\frac{\sqrt{10+2\sqrt 5}(5+\sqrt 5)}{(5-\sqrt 5)(5+\sqrt 5)} \\
&= \frac{5}{4}\cdot\frac{\sqrt{(10+2\sqrt 5)(5+\sqrt 5)^2}}{20} = \frac{\sqrt{(10+2\sqrt 5)(30+10\sqrt 5)}}{16} \\
&= \frac{\sqrt{400+160\sqrt 5}}{16} = \frac{\sqrt{25+10\sqrt 5}}{4}
\end{aligned}\]
である.
- $1$ 辺の長さが $1$ の正四面体は $1$ 辺の長さが $1$ の正三角形 $4$ 枚からなるから,その表面積 $S$ は \[ S = 4\cdot\frac{\sqrt 3}{2} = 2\sqrt 3\] である.
- $1$ 辺の長さが $1$ の正六面体は $1$ 辺の長さが $1$ の正方形 $6$ 枚からなるから,その表面積 $S$ は \[ S = 6\cdot 1 = 6\] である.
- $1$ 辺の長さが $1$ の正八面体は $1$ 辺の長さが $1$ の正三角形 $8$ 枚からなるから,その表面積 $S$ は \[ S = 8\cdot\frac{\sqrt 3}{2} = 4\sqrt 3\] である.
- $1$ 辺の長さが $1$ の正十二面体は $1$ 辺の長さが $1$ の正五角形 $12$ 枚からなるから,その表面積 $S$ は \[ S = 12\cdot\frac{\sqrt{25+10\sqrt 5}}{4} = 3\sqrt{25+10\sqrt 5}\] である.
- $1$ 辺の長さが $1$ の正二十面体は $1$ 辺の長さが $1$ の正三角形 $20$ 枚からなるから,その表面積 $S$ は \[ S = 20\cdot\frac{\sqrt 3}{2} = 10\sqrt 3\] である.
問題《正多面体の体積》
$1$ 辺の長さが $1$ の正四面体, 正六面体, 正八面体, 正十二面体, 正二十面体において, 体積をそれぞれ求めよ.
$1$ 辺の長さが $1$ の正五角形の面積が $\dfrac{\sqrt{25+10\sqrt 5}}{4}$ であること,
および正四面体, 正八面体, 正十二面体, 正二十面体の内接球の半径がそれぞれ $\dfrac{\sqrt 6}{12},$ $\dfrac{\sqrt 6}{6},$ $\dfrac{1}{2}\sqrt{\dfrac{25+11\sqrt 5}{10}},$ $\dfrac{3\sqrt 3+\sqrt{15}}{12}$ であること (こちらを参照) は,
証明なしに使ってよい.
解答例
- $1$ 辺の長さが $1$ の正四面体は底面積が $\dfrac{\sqrt 3}{4},$ 高さが $\dfrac{\sqrt 6}{12}$ (内接球の半径) の正三角錐 $4$ 個に分けられるから, その体積 $V$ は \[ V = 4\cdot\left(\frac{1}{3}\cdot\frac{\sqrt 3}{4}\cdot\frac{\sqrt 6}{12}\right) = \frac{\sqrt 2}{12}\] である.
- $1$ 辺の長さが $1$ の正六面体の体積 $V$ は \[ V = 1^3 = 1\] である.
- $1$ 辺の長さが $1$ の正八面体は辺の長さが $\dfrac{\sqrt 2}{2}$ の $3$ 辺が直角に交わるような正三角錐 $8$ 個に分けられるから, その体積 $V$ は \[ V = 8\cdot\left\{\frac{1}{3}\cdot\frac{1}{2}\left(\frac{\sqrt 2}{2}\right) ^2\cdot\frac{\sqrt 2}{2}\right\} = \frac{\sqrt 2}{3}\] である.
- $1$ 辺の長さが $1$ の正十二面体は底面積が $\dfrac{\sqrt{25+10\sqrt 5}}{4},$ 高さが $\dfrac{1}{2}\sqrt{\dfrac{25+11\sqrt 5}{10}}$ (内接球の半径) の正五角錐 $12$ 個に分けられるから, その体積 $V$ は \[\begin{aligned} V &= 12\cdot\left(\frac{1}{3}\cdot\frac{\sqrt{25+10\sqrt 5}}{4}\cdot\frac{1}{2}\sqrt{\frac{25+11\sqrt 5}{10}}\right) \\ &= \frac{1}{2}\sqrt{\frac{(25+10\sqrt 5)(25+11\sqrt 5)}{10}} = \frac{1}{2}\sqrt{\frac{1175+525\sqrt 5}{10}} \\ &= \frac{1}{2}\sqrt{\frac{470+210\sqrt 5}{4}} = \frac{\sqrt{(15+7\sqrt 5)^2}}{4} = \frac{15+7\sqrt 5}{4} \end{aligned}\] である.
- $1$ 辺の長さが $1$ の正二十面体は底面積が $\dfrac{\sqrt 3}{4},$ 高さが $\dfrac{3\sqrt 3+\sqrt{15}}{12}$ (内接球の半径) の正三角錐 $20$ 個に分けられるから, その体積 $V$ は \[ V = 20\cdot\left(\frac{1}{3}\cdot\frac{\sqrt 3}{4}\cdot\frac{3\sqrt 3+\sqrt{15}}{12}\right) = \frac{15+5\sqrt 5}{12}\] である.
別解
- $1$ 辺の長さが $1$ の正四面体 $\mathrm{ABCD}$ において, 辺 $\mathrm{AB}$ の中点を $\mathrm M$ とおく. このとき, $\mathrm{CD} = 1,$ $\mathrm{CM} = \mathrm{DM} = \dfrac{\sqrt 3}{2}$ となるから, 余弦定理により \[\cos\angle\mathrm{CMD} = \frac{\left(\dfrac{\sqrt 3}{2}\right) ^2+\left(\dfrac{\sqrt 3}{2}\right) ^2-1^2}{2\cdot\dfrac{\sqrt 3}{2}\cdot\dfrac{\sqrt 3}{2}} = \frac{1}{3}\] となり, \[\sin\angle\mathrm{CMD} = \sqrt{1^2-\cos ^2\angle\mathrm{CMD}} = \sqrt{1^2-\left(\frac{1}{3}\right) ^2} = \frac{2\sqrt 2}{3}\] となる. よって, $1$ 辺の長さが $1$ の正四面体の体積 $V$ は \[ V = \frac{1}{3}\cdot\left(\frac{1}{2}\cdot 1^2\cdot\frac{\sqrt 3}{2}\right) \cdot\left(\frac{\sqrt 3}{2}\cdot\frac{2\sqrt 2}{3}\right) = \frac{\sqrt 2}{12}\] である.
- $1$ 辺の長さが $1$ の正八面体は底面の $1$ 辺の長さが $1,$ 高さが $\dfrac{\sqrt 2}{2}$ の正四角錐 $2$ 個に分けられるから, その体積 $V$ は
\[ V = 2\cdot\left(\dfrac{1}{3}\cdot 1^2\cdot\frac{\sqrt 2}{2}\right) = \frac{\sqrt 2}{3}\]
である.
問題《球に内接する正四面体の体積》
半径 $1$ の球に内接する正四面体 $\mathrm{ABCD}$ の体積 $V$ を求めよ.
解答例
正四面体 $\mathrm{ABCD}$ の $1$ 辺の長さを $a$ とおく.
また, 頂点 $\mathrm D$ から面 $\mathrm{ABC}$ に下ろした垂線の足を $\mathrm H$ とおく.
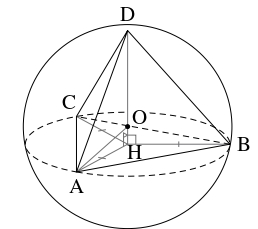 辺 $\mathrm{DH}$ を共有し, 斜辺の長さが等しい $3$ つの直角三角形 $\mathrm{ADH},$ $\mathrm{BDH},$ $\mathrm{CDH}$ は合同であるから,
\[\mathrm{AH} = \mathrm{BH} = \mathrm{CH}\]
である.
よって, $\mathrm H$ は $\triangle\mathrm{ABC}$ の外心であるから, 正弦定理により,
\[\mathrm{AH} = \frac{a}{2\sin 60^\circ} = \frac{a}{\sqrt 3}\]
である.
直角三角形 $\mathrm{ADH}$ に三平方の定理を適用すると,
\[\mathrm{DH} = \sqrt{\mathrm{AD}^2-\mathrm{AH}^2} = \sqrt{a^2-\left(\frac{a}{\sqrt 3}\right) ^2} = \frac{\sqrt 6}{3}a \quad \cdots [1]\]
が得られる.
垂線 $\mathrm{DH}$ は球の中心 $\mathrm O$ を通ることに注意して, 直角三角形 $\mathrm{AOH}$ に三平方の定理を適用すると,
\[\left(\frac{a}{\sqrt 3}\right) ^2+\left(\frac{\sqrt 6}{3}a-1\right) ^2 = 1^2, \quad a^2-\frac{2\sqrt 6}{3}a = 0\]
よって
\[ a = \frac{2\sqrt 6}{3} \quad \cdots [2]\]
が得られる.
したがって,
\[\begin{aligned}
\triangle\mathrm{ABC} &= \frac{1}{2}a^2\sin 60^\circ = \frac{1}{2}\left(\frac{2\sqrt 6}{3}\right)^2\frac{\sqrt 3}{2} = \frac{2\sqrt 3}{3}, \\
\mathrm{DH} &= \frac{\sqrt 6}{3}\cdot\frac{2\sqrt 6}{3} = \frac{4}{3}
\end{aligned}\]
であるから,
\[ V = \frac{1}{3}\triangle\mathrm{ABC}\cdot\mathrm{DH} = \frac{1}{3}\cdot\frac{2\sqrt 3}{3}\cdot\frac{4}{3} = \frac{8\sqrt 3}{27}\]
である.
辺 $\mathrm{DH}$ を共有し, 斜辺の長さが等しい $3$ つの直角三角形 $\mathrm{ADH},$ $\mathrm{BDH},$ $\mathrm{CDH}$ は合同であるから,
\[\mathrm{AH} = \mathrm{BH} = \mathrm{CH}\]
である.
よって, $\mathrm H$ は $\triangle\mathrm{ABC}$ の外心であるから, 正弦定理により,
\[\mathrm{AH} = \frac{a}{2\sin 60^\circ} = \frac{a}{\sqrt 3}\]
である.
直角三角形 $\mathrm{ADH}$ に三平方の定理を適用すると,
\[\mathrm{DH} = \sqrt{\mathrm{AD}^2-\mathrm{AH}^2} = \sqrt{a^2-\left(\frac{a}{\sqrt 3}\right) ^2} = \frac{\sqrt 6}{3}a \quad \cdots [1]\]
が得られる.
垂線 $\mathrm{DH}$ は球の中心 $\mathrm O$ を通ることに注意して, 直角三角形 $\mathrm{AOH}$ に三平方の定理を適用すると,
\[\left(\frac{a}{\sqrt 3}\right) ^2+\left(\frac{\sqrt 6}{3}a-1\right) ^2 = 1^2, \quad a^2-\frac{2\sqrt 6}{3}a = 0\]
よって
\[ a = \frac{2\sqrt 6}{3} \quad \cdots [2]\]
が得られる.
したがって,
\[\begin{aligned}
\triangle\mathrm{ABC} &= \frac{1}{2}a^2\sin 60^\circ = \frac{1}{2}\left(\frac{2\sqrt 6}{3}\right)^2\frac{\sqrt 3}{2} = \frac{2\sqrt 3}{3}, \\
\mathrm{DH} &= \frac{\sqrt 6}{3}\cdot\frac{2\sqrt 6}{3} = \frac{4}{3}
\end{aligned}\]
であるから,
\[ V = \frac{1}{3}\triangle\mathrm{ABC}\cdot\mathrm{DH} = \frac{1}{3}\cdot\frac{2\sqrt 3}{3}\cdot\frac{4}{3} = \frac{8\sqrt 3}{27}\]
である.

別解 1
正四面体 $\mathrm{ABCD}$ の $1$ 辺の長さを $a$ とおく.
また, 辺 $\mathrm{AB}$ の中点を $\mathrm M$ とおく.
このとき,
\[\mathrm{CM} = \mathrm{DM} = \frac{\sqrt 3}{2}a\]
となる.
$\theta = \angle\mathrm{CMD}$ とおき, $\triangle\mathrm{CDM}$ において余弦定理を適用すると,
\[\begin{aligned}
\cos\theta &= \frac{\left(\dfrac{\sqrt 3}{2}a\right) ^2+\left(\dfrac{\sqrt 3}{2}a\right) ^2-a^2}{2\cdot\dfrac{\sqrt 3}{2}a\cdot\dfrac{\sqrt 3}{2}a} \\
&= \frac{(\sqrt 3)^2+(\sqrt 3)^2-2^2}{2\cdot\sqrt 3\cdot\sqrt 3} = \frac{1}{3}, \\
\sin\theta &= \sqrt{1-\cos ^2\theta} = \sqrt{1-\left(\frac{1}{3}\right) ^2} = \frac{2\sqrt 2}{3}
\end{aligned}\]
が得られる.
よって, 頂点 $\mathrm D$ から面 $\mathrm{ABC}$ に下ろした垂線の足を $\mathrm H$ とおくと,
\[\mathrm{DH} = \mathrm{DM}\sin\theta = \frac{\sqrt 3}{2}a\cdot\frac{2\sqrt 2}{3} = \frac{\sqrt 6}{3}a \quad \cdots [1]\]
となる.
以下, 解答例と同様.
別解 2: $[1]$ 以降
球の中心を $\mathrm O$ とおく.
$4$ つの四面体 $\mathrm{OABC},$ $\mathrm{OBCD},$ $\mathrm{OCDA},$ $\mathrm{ODAB}$ は合同である.
よって, その体積を $W$ とおくと $V = 4W$ となるので,
\[\dfrac{1}{3}\triangle\mathrm{ABC}\cdot\mathrm{DH} = 4\cdot\frac{1}{3}\triangle\mathrm{ABC}\cdot\mathrm{OH}\]
から
\[\mathrm{DH} = 4\mathrm{OH}\]
が得られる.
垂線 $\mathrm{DH}$ が点 $\mathrm O$ を通ることに注意すると,
\[\begin{aligned}
\mathrm{DH} &= \frac{4}{3}\mathrm{OD} = \frac{4}{3}, \\
a &= \frac{3}{\sqrt 6}\mathrm{DH} = \frac{3}{\sqrt 6}\cdot\frac{4}{3} = \frac{2\sqrt 6}{3}
\end{aligned}\]
が得られる.
以下, 解答例と同様.
別解 3: $[2]$ 以降
$1$ 辺の長さが $a$ の正四面体 $\mathrm{ABCD}$ は $1$ 辺の長さが $\dfrac{a}{\sqrt 2}$ の立方体 $\mathrm{AKDL}\text{-}\mathrm{MBNC}$ に内接させることができる.
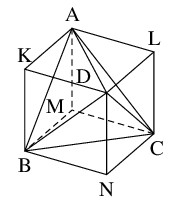 よって, 正四面体 $\mathrm{ABCD}$ はこの立方体から $4$ 個の合同な三角錐を取り除いたものであり, 各三角錐の体積は立方体の体積 $W$ の $\dfrac{1}{6}$ にあたるから, 求める体積は,
\[\begin{aligned}
V &= W-4\cdot\frac{W}{6} = \frac{1}{3}W = \frac{1}{3}\left(\frac{a}{\sqrt 2}\right) ^3 = \frac{\sqrt 2}{12}a^3 \\
&= \frac{\sqrt 2}{12}\left(\frac{2\sqrt 6}{3}\right) ^3 = \frac{8\sqrt 3}{27}
\end{aligned}\]
である.
よって, 正四面体 $\mathrm{ABCD}$ はこの立方体から $4$ 個の合同な三角錐を取り除いたものであり, 各三角錐の体積は立方体の体積 $W$ の $\dfrac{1}{6}$ にあたるから, 求める体積は,
\[\begin{aligned}
V &= W-4\cdot\frac{W}{6} = \frac{1}{3}W = \frac{1}{3}\left(\frac{a}{\sqrt 2}\right) ^3 = \frac{\sqrt 2}{12}a^3 \\
&= \frac{\sqrt 2}{12}\left(\frac{2\sqrt 6}{3}\right) ^3 = \frac{8\sqrt 3}{27}
\end{aligned}\]
である.

問題《等面四面体の存在と計量》
$\triangle\mathrm{ABC}$ を鋭角三角形とし, $a = \mathrm{BC},$ $b = \mathrm{CA},$ $c = \mathrm{AB}$ とおく.
- (1)
- 各面が $\triangle\mathrm{ABC}$ と合同な四面体 $T$ が存在することを示せ.
- (2)
- $T$ の体積 $V$ を求めよ.
- (3)
- $T$ の外接球の半径 $R$ を求めよ.
- (4)
- $T$ の表面積 $S$ を求めよ.
- (5)
- $T$ の内接球の半径 $r$ を求めよ.
(参考: $1999$ 京都大)
解答例
- (1)
- $a,$ $b,$ $c$ を面の対角線の長さとする直方体の存在, つまり
\[y^2+z^2 = a^2, \quad z^2+x^2 = b^2, \quad x^2+y^2 = c^2\]
なる正の数 $x,$ $y,$ $z$ の存在を示せばよい.
これら $3$ 式の辺々を加えて両辺を $2$ で割ると \[ x^2+y^2+z^2 = \frac{a^2+b^2+c^2}{2}\] となるから, これは \[\begin{aligned} x^2 &= \dfrac{b^2+c^2-a^2}{2}, \\ y^2 &= \dfrac{c^2+a^2-b^2}{2}, \\ z^2 &= \dfrac{a^2+b^2-c^2}{2} \end{aligned}\] と同値であり, 条件からこれら $3$ 式の右辺は正であることに注意すると, \[\begin{aligned} x &= \sqrt{\frac{b^2+c^2-a^2}{2}}, \\ y &= \sqrt{\frac{c^2+a^2-b^2}{2}}, \\ z &= \sqrt{\frac{a^2+b^2-c^2}{2}} \end{aligned}\] が条件を満たすことがわかる.
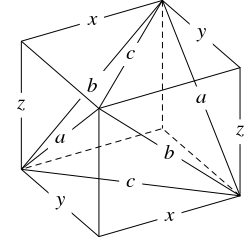
- (2)
- $T$ は (1) の直方体から $4$ つの角 (互いに合同な三角錐) を取り除いて得られるから, その体積は \[\begin{aligned} V &= xyz-4\cdot\frac{1}{3}\cdot\frac{1}{2}xy\cdot z = \frac{1}{3}xyz \\ &= \frac{\sqrt{2(b^2+c^2-a^2)(c^2+a^2-b^2)(a^2+b^2-c^2)}}{12} \end{aligned}\] である.
- (3)
- $T$ の外接球の直径は (1) の直方体の対角線の長さに等しいから, $T$ の外接球の半径は \[ R = \frac{1}{2}\sqrt{x^2+y^2+z^2} = \sqrt{\frac{a^2+b^2+c^2}{8}}\] である.
- (4)
- $T$ の表面積は,「ヘロンの公式」により, \[\begin{aligned} S &= 4\triangle\mathrm{ABC} \\ &= \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \end{aligned}\] である.
- (5)
- $V = \dfrac{1}{3}Sr$ であるから, $T$ の内接球の半径は \[\begin{aligned} r &= \frac{3V}{S} \\ &= \sqrt{\frac{(b^2+c^2-a^2)(c^2+a^2-b^2)(a^2+b^2-c^2)}{8(a+b+c)(b+c-a)(c+a-b)(a+b-c)}} \end{aligned}\] である.
参考
- 各面が合同な四面体を「等面四面体」(equifacial tetrahedron) と呼ぶ.
- $4$ つの面の面積が等しい四面体は「等面四面体」であることが知られている.
- 正四面体は, 向かい合う $2$ 辺がすべて互いに垂直な「等面四面体」として特徴付けられる (こちらを参照).
- 「等面四面体」の重心, 外心, 内心は一致する. また, 重心, 外心, 内心のうち $2$ つが一致する四面体は等面四面体であることが知られている.
- 「等面四面体」の内接球と各面との接点は, その面の外心であることが知られている.
