三角関数の倍角の公式
$2$ 倍角の公式
定理《三角関数の $2$ 倍角・半角の公式》
- (1)
- 角 $\theta$ に対して \[\begin{aligned} \cos 2\theta &= \cos ^2\theta -\sin ^2\theta \\ &= 2\cos ^2\theta -1 = 1-2\sin ^2\theta, \\ \sin 2\theta &= 2\sin\theta\cos\theta \\ \tan 2\theta &= \frac{2\tan\theta}{1-\tan ^2\theta} \quad \left(\theta,\ 2\theta \neq \dfrac{2k+1}{2}\pi,\ k\text{: 整数}\right) \end{aligned}\] が成り立つ.
- (2)
- 角 $\theta$ に対して \[\begin{aligned} \cos ^2\frac{\theta}{2} &= \frac{1+\cos\theta}{2}, \\ \sin ^2\frac{\theta}{2} &= \frac{1-\cos\theta}{2}, \\ \tan ^2\frac{\theta}{2} &= \frac{1-\cos\theta}{1+\cos\theta} \quad \left(\theta,\ \frac{\theta}{2} \neq \dfrac{2k+1}{2}\pi,\ k\text{: 整数}\right) \end{aligned}\] が成り立つ.
証明
- (1)
- 加法定理において $\alpha = \beta = \theta$ とすると, 直ちに得られる.
- (2)
- (1) において $\theta$ を $\dfrac{\theta}{2}$ に置き換えると, 直ちに得られる.
問題《モリーの法則》
正の整数 $n,$ 実数 $\theta$ に対して
\[\cos\theta\cos 2\theta\cdots\cos 2^{n-1}\theta = \frac{\sin 2^n\theta}{2^n\sin\theta}\]
が成り立つこと, 特に $\theta = \dfrac{\pi}{2^n+1}$ のとき
\[\cos\theta\cos 2\theta\cdots\cos 2^{n-1}\theta = \frac{1}{2^n}\]
が成り立つことを示せ.
(参考: $2015$ 横浜市立大)
解答例
倍角の公式により
\[\cos 2^{k-1}\theta = \frac{\sin 2^k\theta}{2\sin 2^{k-1}\theta} \quad (0 \leqq k \leqq n-1)\]
であるから, 辺々を掛け合わせると
\[\begin{aligned}
\cos\theta\cos 2\theta\cdots\cos 2^{n-1}\theta &= \frac{\sin 2\theta}{2\sin\theta}\cdot\frac{\sin 4\theta}{2\sin 2\theta}\cdot\cdots\cdot\frac{\sin 2^n\theta}{2\sin 2^{n-1}\theta} \\
&= \frac{\sin 2^n\theta}{2^n\sin\theta}
\end{aligned}\]
が得られる.
特に $\theta = \dfrac{\pi}{2^n+1}$ のとき, $2^n\theta = \pi -\theta$ であるから,
\[\cos\theta\cos 2\theta\cdots\cos 2^{n-1}\theta = \frac{\sin (\pi -\theta )}{2^n\sin\theta} = \frac{\sin\theta}{2^n\sin\theta} = \frac{1}{2^n}\]
が成り立つ.
参考
- $\cos 20^\circ\cos 40^\circ\cos 80^\circ = \dfrac{1}{8}$ は「モリーの法則」(Morrie's law) として知られている.
- 本問の等式から,「ヴィエトの公式」(Viète's formula) が得られる (こちらを参照).
問題《円に接する正多角形の周の長さの関係式》
- (1)
- 単位円に外接する正 $n$ 角形の周の長さを $L_n,$ 単位円に内接する正 $n$ 角形の周の長さを $l_n$ とおく. \[ L_{2n} = \frac{2L_nl_n}{L_n+l_n}, \quad l_{2n} = \sqrt{L_{2n}l_n}\] が成り立つことを示せ.
- (2)
- (1) の結果を利用して $L_{12},$ $l_{12}$ の値を求め, \[ 3(\sqrt 6-\sqrt 2) < \pi < 12(2-\sqrt 3)\] であることを示せ.
解答例
- (1)
- 定義により, \[ L_n = 2n\tan\frac{\pi}{n}, \quad l_n = 2n\sin\frac{\pi}{n}\] である. よって, 倍角の公式により \[\begin{aligned} \frac{2L_nl_n}{L_n+l_n} &= \frac{2\cdot 2n\tan\dfrac{\pi}{n}\cdot 2n\sin\dfrac{\pi}{n}}{2n\tan\dfrac{\pi}{n}+2n\sin\dfrac{\pi}{n}} \\ &= \frac{4n\sin\dfrac{\pi}{n}}{1+\cos\dfrac{\pi}{n}} \\ &= \frac{4n\cdot 2\sin\dfrac{\pi}{2n}\cos\dfrac{\pi}{2n}}{2\cos ^2\dfrac{\pi}{2n}} \\ &= 2\cdot 2n\tan\frac{\pi}{2n} \\ &= L_{2n} \end{aligned}\] が成り立つ. また, 倍角の公式により \[\begin{aligned} L_{2n}l_n &= 2\cdot 2n\tan\frac{\pi}{2n}\cdot 2n\sin\frac{\pi}{n} \\ &= 8n^2\tan\frac{\pi}{2n}\cdot 2\sin\frac{\pi}{2n}\cos\frac{\pi}{2n} \\ &= 16n^2\sin ^2\frac{\pi}{2n} \end{aligned}\] であるから, \[\sqrt{L_{2n}l_n} = 2\cdot 2n\sin\frac{\pi}{2n} = l_{2n}\] が成り立つ.
- (2)
- 単位円に外接する正六角形, 内接する正六角形の $1$ 辺の長さはそれぞれ $\dfrac{2}{\sqrt 3},$ $1$ であるから, \[ L_6 = 6\cdot\frac{2}{\sqrt 3} = 4\sqrt 3, \quad l_6 = 6\cdot 1 = 6\] である. よって, (1) の関係式により, \[\begin{aligned} L_{12} &= \frac{2\cdot 4\sqrt 3\cdot 6}{4\sqrt 3+6} = \frac{24}{2+\sqrt 3} = 24(2-\sqrt 3), \\ l_{12} &= \sqrt{24(2-\sqrt 3)\cdot 6} = 6\sqrt{8-2\sqrt{12}} = 6(\sqrt 6-\sqrt 2) \end{aligned}\] である. ゆえに, $l_{12} < 2\pi < L_{12}$ つまり $\dfrac{l_{12}}{2} < \pi < \dfrac{L_{12}}{2}$ から, \[ 3(\sqrt 6-\sqrt 2) < \pi < 12(2-\sqrt 3)\] である.
問題《正多角形の面積》
$1$ 辺の長さが $a$ の正 $n$ 角形について,
- (1)
- 外接円の半径 $R$ を $a$ と $\dfrac{\pi}{n}$ の三角比を用いて表せ.
- (2)
- 面積 $S$ を $a,$ $n$ と $\dfrac{\pi}{n}$ の三角比を用いて表せ.
解答例
- (1)
- 正 $n$ 角形の外接円において, 正 $n$ 角形の $1$ 辺に対する中心角は $\dfrac{2\pi}{n}$ であるから, 円周角の定理により, その弧に対する円周角は $\dfrac{\pi}{n}$ である. よって, 正 $n$ 角形の $1$ 辺の長さが $a$ であるとき, 正弦定理により, その外接円の半径 $R$ は \[ R = \frac{a}{2\sin\dfrac{\pi}{n}}\] と表される.
- (2)
- 倍角の公式により, $1$ 辺の長さが $a$ である正 $n$ 角形の面積 $S$ は \[\begin{aligned} S &= n\cdot\frac{1}{2}R^2\sin\frac{2\pi}{n} \\ &= n\cdot\frac{1}{2}\cdot\frac{a^2}{4\sin ^2\dfrac{\pi}{n}}\cdot 2\sin\frac{\pi}{n}\cos\frac{\pi}{n} \\ &= \frac{na^2\cos\dfrac{\pi}{n}}{4\sin\dfrac{\pi}{n}} = \frac{na^2}{4\tan\dfrac{\pi}{n}} \end{aligned}\] と表される.
参考
有限種類の合同な正多角形で平面を隙間も重なりもなく敷き詰めて, 各頂点で辺が同じ形状で交わるようにする方法は, 全部で $3+8 = 11$ 通りある.
その際に用いられる正多角形のうち, 辺の数が最も多い正多角形は正十二角形である (こちらを参照).
問題《斜方投射の最大水平到達距離》
時刻 $0$ に高さ $0$ の地点から, 水平面に対して $\theta$ $\left( 0 < \theta < \dfrac{\pi}{2}\right)$ の角をなす方向に初速 $v_0$ $(v_0 > 0)$ で物体を投げるとき, 時刻 $t$ における物体の水平移動距離 $x$ と高さ $y$ は, ある正の数 $g$ を用いて
\[\begin{aligned}
x &= v_0\cos\theta\cdot t \quad \cdots [1], \\
y &= v_0\sin\theta\cdot t-\frac{1}{2}gt^2 \quad \cdots [2]
\end{aligned}\]
と表されるという.
- (1)
- $y$ を $x$ の $2$ 次関数として表せ.
- (2)
- 物体が再び高さ $0$ の地点に到達するときの時刻と水平移動距離を求めよ.
- (3)
- (2) の距離が最大になるとき, $\theta$ の値を求めよ.
解答例
- (1)
- $[1]$ により $t = \dfrac{x}{v_0\cos\theta}$ であるから, これを $[2]$ に代入すると \[\begin{aligned} y &= v_0\sin\theta\cdot\frac{x}{v_0\cos\theta}-\frac{1}{2}g\cdot\dfrac{x^2}{v_0{}^2\cos ^2\theta} \\ &= x\tan\theta -\frac{g}{2v_0{}^2\cos ^2\theta}x^2 \end{aligned}\] が得られる.
- (2)
- \[\begin{aligned} y &= -\frac{g}{2v_0{}^2\cos ^2\theta}x\left( x-\frac{2v_0{}^2\cos ^2\theta}{g}\cdot\tan\theta\right) \\ &= -\frac{g}{2v_0{}^2\cos ^2\theta}x\left( x-\frac{2v_0{}^2\sin\theta\cos\theta}{g}\right) \\ &= -\frac{g}{2v_0{}^2\cos ^2\theta}x\left( x-\frac{v_0{}^2\sin 2\theta}{g}\right) \end{aligned}\] であるから, 物体が再び高さ $0$ の地点に到達するときの水平移動距離は $x = \dfrac{v_0{}^2\sin 2\theta}{g},$ 時刻は $t = \dfrac{2v_0\sin\theta}{g}$ である.
- (3)
- $v_0 > 0,$ $g > 0$ であり, $0 < \theta < \dfrac{\pi}{2}$ から $0 < 2\theta < \pi,$ よって $0 < \sin 2\theta \leqq 1$ であるので, $\dfrac{v_0{}^2\sin 2\theta}{g}$ は $\sin 2\theta = 1,$ $2\theta = \dfrac{\pi}{2},$ つまり $\theta = \dfrac{\pi}{4}$ のとき最大になる.
参考
古典力学において, 水平面に対して斜め方向に物体を投げたときの運動を「斜方投射」(projectile motion) と呼ぶ.
問題《ブレートシュナイダーの公式》
四角形 $\mathrm{ABCD}$ において, $a = \mathrm{AB},$ $b = \mathrm{BC},$ $c = \mathrm{CD},$ $d = \mathrm{DA},$ $s = \dfrac{a+b+c+d}{2},$ $B = \angle\mathrm{ABC},$ $D = \angle\mathrm{CDA}$ とおき, 面積を $S$ とおく.
- (1)
- $a,$ $b,$ $c,$ $d,$ $\sin B,$ $\sin D$ を用いて $S^2$ を表せ.
- (2)
- $a,$ $b,$ $c,$ $d,$ $\cos B,$ $\cos D$ を用いて $\dfrac{1}{16}(a^2+b^2-c^2-d^2)^2$ を表せ.
- (3)
- $S$ は \[ S = \sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos ^2\frac{B+D}{2}}\] と表されることを示せ.
- (4)
- $4$ 辺の長さ $a,$ $b,$ $c,$ $d$ を固定しながら四角形 $\mathrm{ABCD}$ を変形するとき, その面積 $S$ は四角形が円に内接するときに限り最大になることを示せ.
解答例
- (1)
- \[ S = \triangle\mathrm{ABC}+\triangle\mathrm{CDA} = \frac{1}{2}ab\sin B+\frac{1}{2}cd\sin D\] であるから, \[ S^2 = \frac{1}{4}a^2b^2\sin ^2B+\frac{1}{4}c^2d^2\sin ^2D+\frac{1}{2}abcd\sin B\sin D\] が成り立つ.
- (2)
- $\triangle\mathrm{ABC},$ $\triangle\mathrm{CDA}$ に余弦定理を適用すると \[\mathrm{AC}^2 = a^2+b^2-2ab\cos B = c^2+d^2-2cd\cos D\] となるから, \[ a^2+b^2-c^2-d^2 = 2(ab\cos B-cd\cos D),\] よって \[\begin{aligned} &\frac{1}{16}(a^2+b^2-c^2-d^2)^2 \\ &= \frac{1}{4}a^2b^2\cos ^2B+\frac{1}{4}c^2d^2\!\cos ^2D-\frac{1}{2}abcd\cos B\cos D \end{aligned}\] が得られる.
- (3)
- (1), (2) で得られた等式の辺々を加えると, \[\begin{aligned} &S^2+\frac{1}{16}(a^2+b^2-c^2-d^2)^2 \\ &= \frac{1}{4}a^2b^2(\cos ^2\!B+\sin ^2B)+\frac{1}{4}c^2d^2(\cos ^2D+\sin ^2D) \\ &\quad -\frac{1}{2}abcd(\cos B\cos D-\sin B\sin D) \\ &= \frac{1}{4}a^2b^2+\frac{1}{4}c^2d^2-\frac{1}{2}abcd\cos (B+D) \\ &= \frac{1}{4}a^2b^2+\frac{1}{4}c^2d^2+\frac{1}{2}abcd-abcd\cos ^2\frac{B+D}{2} \\ &= \frac{1}{4}(ab+cd)^2-abcd\cos ^2\frac{B+D}{2} \end{aligned}\] となるから, \[\begin{aligned} &S^2+abcd\cos ^2\frac{B+D}{2} \\ &= \frac{1}{16}\{ 4(ab+cd)^2-(a^2+b^2-c^2-d^2)^2\} \\ &= \frac{1}{16}\{ 2(ab+cd)-(a^2+b^2-c^2-d^2)\} \\ &\qquad \{ 2(ab+cd)+(a^2+b^2-c^2-d^2)\} \\ &= \frac{1}{16}\{ (c+d)^2-(a-b)^2\}\{ (a+b)^2-(c-d)^2\} \\ &= \frac{-a+b+c+d}{2}\cdot\frac{a-b+c+d}{2} \\ &\qquad \cdot\frac{a+b-c+d}{2}\cdot\frac{a+b+c-d}{2} \\ &= (s-a)(s-b)(s-c)(s-d) \end{aligned}\] が成り立つ. よって, \[ S^2 = (s-a)(s-b)(s-c)(s-d)-abcd\cos ^2\frac{B+D}{2}\] であるから, 両辺の平方根をとると \[ S = \sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos ^2\frac{B+D}{2}}\] が得られる.
- (4)
- (3) の結果により, $S$ は \[\cos ^2\frac{B+D}{2} = 0, \quad \frac{B+D}{2} = \frac{\pi}{2}, \quad B+D = \pi\] のとき, つまり四角形 $\mathrm{ABCD}$ が円に内接するときに限り最大値をとる.
参考
- (3) の結果は「ブレートシュナイダーの公式」(Bretschneider's formula) として知られている.
- この公式は「ブラーマグプタの公式」(Brahmagupta's formula) \[ S = \sqrt{(s-a)(s-b)(s-c)(s-d)}\] の一般化になっている (こちらを参照).
- $\mathrm{AB} = a,$ $\mathrm{BC} = b,$ $\mathrm{CD} = c,$ $\mathrm{DA} = d,$ $\mathrm{AC} = p,$ $\mathrm{BD} = q$ である四角形 $\mathrm{ABCD}$ の面積 $S$ は \[ S = \frac{1}{2}\sqrt{p^2q^2-\left(\frac{a^2-b^2+c^2-d^2}{2}\right) ^2}\] と表されることが知られている.
問題《ピタゴラスの $3$ つ組の公式の三角法的証明》
正の整数 $a,$ $b,$ $c$ $(a < c,$ $b < c)$ を $3$ 辺の長さとする直角三角形において, $\theta$ を $\tan\theta = \dfrac{b}{a}$ なる鋭角とし, $t = \tan\dfrac{\theta}{2}$ とおく.
- (1)
- $t$ を用いて $\cos\theta,$ $\sin\theta,$ $\dfrac{1-\cos\theta}{1+\cos\theta}$ を表せ.
- (2)
- $t$ は有理数であることを示せ.
- (3)
- $3$ 辺の長さの比は互いに素な正の整数 $m,$ $n$ $(m > n)$ を用いて \[ a:b:c = (m^2-n^2):2mn:(m^2+n^2)\] と表されることを示せ.
解答例
- (1)
- 倍角の公式により \[\tan\theta = \frac{2t}{1-t^2}\] であるから, \[\begin{aligned} &\cos ^2\theta = \frac{1}{1+\tan ^2\theta} = \frac{1}{1+\dfrac{4t^2}{(1-t^2)^2}} \\ &= \frac{(1-t^2)^2}{(1-t^2)^2+4t^2} = \frac{(1-t^2)^2}{(1+t^2)^2} = \left(\frac{1-t^2}{1+t^2}\right) ^2, \\ &\sin ^2\theta = 1-\cos ^2\theta = 1-\frac{(1-t^2)^2}{(1+t^2)^2} \\ &= \frac{(1+t^2)^2-(1-t^2)^2}{(1+t^2)^2} = \frac{4t^2}{(1+t^2)^2} = \left(\frac{2t}{1+t^2}\right) ^2 \end{aligned}\] が成り立つ. よって, $0 < \theta < \dfrac{\pi}{2}$ から $\cos\theta,$ $\sin\theta > 0,$ $0 < t < 1$ であるので, \[\begin{aligned} &\cos\theta = \frac{1-t^2}{1+t^2}, \quad \sin\theta = \frac{2t}{1+t^2} \quad \cdots [1], \\ &\frac{1-\cos\theta}{1+\cos\theta} = \frac{(1+t^2)-(1-t^2)}{(1+t^2)+(1-t^2)} = t^2 \quad \cdots [2] \end{aligned}\] が得られる.
- (2)
- 仮定から $\cos\theta$ は有理数であるので, $[2]$ から $t^2$ は有理数である. さらに, $\sin\theta$ も有理数であるので, $[1]$ から $t = \dfrac{1+t^2}{2}\sin\theta$ も有理数である.
- (3)
- $0 < t < 1$ に注意して, 互いに素な正の整数 $m,$ $n$ $(m > n)$ を用いて $t = \dfrac{n}{m}$ とおくと, $[1]$ から \[\begin{aligned} \frac{a}{c} &= \cos\theta = \frac{1-\dfrac{n^2}{m^2}}{1+\dfrac{n^2}{m^2}} = \frac{m^2-n^2}{m^2+n^2}, \\ \frac{b}{c} &= \sin\theta = \frac{2\cdot\dfrac{n}{m}}{1+\dfrac{n^2}{m^2}} = \frac{2mn}{m^2+n^2} \end{aligned}\] となり, \[ a:b:c = (m^2-n^2):2mn:(m^2+n^2)\] となる.
参考
$3$ 倍角の公式
定理《三角関数の $3$ 倍角の公式》
すべての角 $\theta$ に対して
\[\begin{aligned}
\cos 3\theta &= 4\cos ^3\theta -3\cos\theta, \\
\sin 3\theta &= 3\sin\theta -4\sin ^3\theta, \\
\tan 3\theta &= \frac{3\tan\theta -\tan ^3\theta}{1-3\tan ^2\theta}
\end{aligned}\]
が成り立つ.
証明
余弦, 正弦については, こちらを参照.
正接については, 加法定理, 倍角の公式により
\[\begin{aligned}
\tan3\theta &= \tan (2\theta +\theta ) = \frac{\tan 2\theta +\tan\theta}{1-\tan 2\theta\tan\theta} \\
&= \frac{\dfrac{2\tan\theta}{1-\tan ^2\theta}+\tan\theta}{1-\dfrac{2\tan\theta}{1-\tan ^2\theta}\tan\theta} = \frac{2\tan\theta +\tan\theta (1-\tan ^2\theta )}{(1-\tan ^2\theta )-2\tan ^2\theta} \\
&= \frac{3\tan\theta -\tan ^3\theta}{1-3\tan ^2\theta}
\end{aligned}\]
と示される.
別証明
正接については,
\[\begin{aligned}
\tan3\theta &= \frac{\sin 3\theta}{\cos 3\theta} = \frac{3\sin\theta -4\sin ^3\theta}{4\cos ^3\theta -3\cos\theta}\\
&= \frac{\sin\theta}{\cos\theta}\cdot\frac{3-4\sin ^2\theta}{4\cos ^2\theta -3} = \tan\theta\cdot\frac{4\cos^2\theta -1}{4\cos^2\theta -3} \\
&= \tan\theta\cdot\frac{\dfrac{4}{1+\tan ^2\theta}-1}{\dfrac{4}{1+\tan ^2\theta}-3} = \tan\theta\cdot\frac{4-(1+\tan ^2\theta )}{4-3(1+\tan ^2\theta )} \\
&= \tan\theta\cdot\frac{3-\tan ^2\theta}{1-3\tan ^2\theta} = \frac{3\tan\theta -\tan ^3\theta}{1-3\tan ^2\theta}
\end{aligned}\]
と示される.
問題《正五角形の対角線の長さ》
- (1)
- 実数 $\theta$ に対して $\cos 3\theta = 4\cos ^3\theta -3\cos\theta$ が成り立つことを示せ.
- (2)
- $a = \cos\dfrac{2\pi}{5}$ の値を求めよ.
- (3)
- $1$ 辺の長さが $1$ の正五角形の対角線の長さを求めよ.
解答例
- (1)
- 加法定理,$2$ 倍角の公式により, \[\begin{aligned} \cos 3\theta &= \cos (\theta +2\theta ) = \cos\theta\cos 2\theta -\sin\theta\sin 2\theta \\ &= \cos\theta (2\cos ^2\theta -1)-\sin\theta\cdot 2\sin\theta\cos\theta \\ &= 2\cos ^3\theta -\cos\theta -2\cos\theta (1-\cos ^2\theta ) \\ &= 4\cos ^3\theta -3\cos\theta \quad \cdots [1] \end{aligned}\] が成り立つ.
- (2)
- $\theta = \dfrac{2\pi}{5}$ とおくと, $3\theta +2\theta = 2\pi$ となり, $\cos 3\theta = \cos 2\theta$ となる. よって, 倍角の公式と $[1]$ から \[\begin{aligned} 4a^3-3a &= 2a^2-1 \\ 4a^3-2a^2-3a+1 &= 0 \\ (a-1)(4a^2+2a-1) &= 0 \end{aligned}\] であるので, $0 < a < 1$ であることに注意すると $a = \dfrac{-1+\sqrt 5}{4}$ が得られる.
- (3)
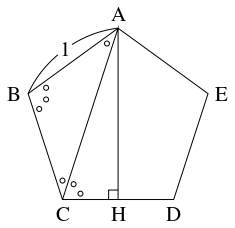
- $1$ 辺の長さが $1$ の正五角形 $\mathrm{ABCDE}$ の頂点 $\mathrm A$ から辺 $\mathrm{CD}$ に下ろした垂線の足を $\mathrm H$ とおく.
$\angle\mathrm{ABC} = \dfrac{(5-2)\pi}{5} = \dfrac{3\pi}{5}$ と $\mathrm{BA} = \mathrm{BC}$ から, $\angle\mathrm{BCA} = (\pi -\angle\mathrm{ABC})\div 2 = \dfrac{\pi}{5}$ である. よって, $\angle\mathrm{ACH} = \angle\mathrm{BCD}-\angle\mathrm{BCA} = \dfrac{2\pi}{5}$ から $\cos\dfrac{2\pi}{5} = \cos\angle\mathrm{ACH} = \dfrac{\mathrm{CH}}{\mathrm{AC}}$ であるので, \[\begin{aligned} \mathrm{AC} &= \mathrm{CH}\div\cos\dfrac{2\pi}{5} = \dfrac{1}{2}\cdot\dfrac{4}{\sqrt 5-1} \\ &= \dfrac{2(\sqrt 5+1)}{4} = \dfrac{1+\sqrt 5}{2} \end{aligned}\] である.
別解
- (1)
- $c = \cos\theta,$ $s = \sin\theta$ とおく. ド・モアブルの定理により \[\begin{aligned} &\cos 3\theta +i\sin 3\theta = (c+si)^3 \\ &= c^3+3c^2(si)+3c(-s^2)-s^3i \\ &= (c^3-3cs^2)+(3c^2s-s^3)i \\ &= \{ c^3-3c(1-c^2)\} +\{ 3(1-s^2)s-s^3\} i \\ &= (4c^3-3c)+(3s-4s^3)i \end{aligned}\] であるから, 両辺の実部を比較すると, 求める等式が得られる.
参考
- 正五角形の辺と対角線の長さの比 $1:\dfrac{1+\sqrt 5}{2}$ を「黄金比」(golden ratio) と呼び, $\dfrac{1+\sqrt 5}{2}$ を「黄金数」(golden number) と呼ぶ.
- \[\begin{aligned} \cos 2\theta &= 2\cos ^2\theta -1, & \sin 2\theta &= (2\cos\theta )\sin\theta, \\ \cos 3\theta &= 4\cos ^3\theta -3\cos\theta, & \sin 3\theta &= (4\cos ^2\theta -1)\sin\theta \end{aligned}\] のように, 各正の整数 $n$ に対し, $\cos n\theta$ はある $n$ 次多項式 $T_n(x)$ を用いて $\cos n\theta = T_n(\cos\theta )$ と表せ, $\sin n\theta$ はある $n-1$ 次多項式 $U_{n-1}(x)$ を用いて $\sin n\theta = U_{n-1}(\cos\theta )\sin\theta$ と表せることが知られている. $T_n(x),$ $U_{n-1}(x)$ は, それぞれ「第一種チェビシェフ多項式」,「第二種チェビシェフ多項式」と呼ばれ, あわせて「チェビシェフ多項式」(Chebyshev polynomial) と呼ばれる.
問題《正七角形調和》
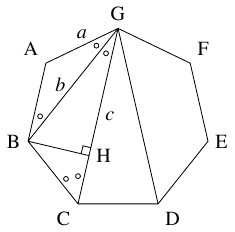
正七角形 $\mathrm{ABCDEFG}$ において $a = \mathrm{GA},$ $b = \mathrm{GB},$ $c = \mathrm{GC}$ とおき, $\theta = \dfrac{\pi}{7}$ とおく.
- (1)
- $\triangle\mathrm{GAB}$ と $\triangle\mathrm{GBC}$ に着目して, $b = 2a\cos\theta$ と $c = a(4\cos ^2\theta -1)$ を示せ.
- (2)
- $\sin 3\theta$ と $\sin 4\theta$ を $\cos\theta$ の多項式と $\sin\theta$ の積の形に表せ.
- (3)
- $\cos\theta$ を解にもつ $3$ 次方程式を $1$ つ求めよ.
- (4)
- $a^{-1} = b^{-1}+c^{-1}$ が成り立つことを示せ.
解答例
- (1)
- $\triangle\mathrm{GAB}$ は頂角が $\dfrac{5\pi}{7},$ 底角が $\theta = \dfrac{\pi}{7}$ の二等辺三角形であるから,
\[ b = \mathrm{GB} = 2\mathrm{GA}\cos\angle\mathrm{AGB} = 2a\cos\theta \quad \cdots [1]\]
が成り立つ.
等脚台形 $\mathrm{ABCG}$ に着目すると, $\angle\mathrm{BGC} = \angle\mathrm{ABG} = \theta,$ $\angle\mathrm{BCG} = \angle\mathrm{AGC} = \angle\mathrm{AGB}+\angle\mathrm{BGC} = 2\theta$ がわかる. 点 $\mathrm B$ から $\mathrm{GC}$ に下ろした垂線の足を $\mathrm H$ とおくと, \[\begin{aligned} c &= \mathrm{GC} = \mathrm{GH}+\mathrm{HC} \\ &= \mathrm{GB}\cos\angle\mathrm{BGC}+\mathrm{BC}\cos\angle\mathrm{BCG} \\ &= b\cos\theta +a\cos 2\theta \\ &= 2a\cos ^2\theta +a(2\cos ^2\theta -1) \\ &= a(4\cos ^2\theta -1) \quad \cdots [2] \end{aligned}\] となる.
- (2)
- 加法定理と $2$ 倍角の公式により, \[\begin{aligned} \sin 3\theta &= \sin (2\theta +\theta ) = \sin 2\theta\cos\theta +\cos 2\theta\sin\theta \\ &= (2\sin\theta\cos\theta )\cos\theta +(2\cos ^2\theta -1)\sin\theta \\ &= (4\cos ^2\theta -1)\sin\theta \quad \cdots [3], \\ \sin 4\theta &= \sin 2(2\theta ) = 2\sin 2\theta\cos 2\theta \\ &= 2(2\sin\theta\cos\theta )(2\cos ^2\theta -1) \\ &= (8\cos ^3\theta -4\cos\theta )\sin\theta \quad \cdots [4] \end{aligned}\] が成り立つ.
- (3)
- $\theta = \dfrac{\pi}{7}$ から $3\theta +4\theta = \pi$ であるので, \[\sin 4\theta = \sin 3\theta\] が成り立つ. ここに $[3]$ と $[4]$ を代入して整理すると \[ (8\cos ^3\theta -4\cos ^2\theta -4\cos\theta +1)\sin\theta = 0\] となり, $\sin\theta \neq 0$ から \[ 8\cos ^3\theta -4\cos ^2\theta -4\cos\theta +1 = 0 \quad \cdots [5]\] となる. $\cos\theta$ を解にもつ $3$ 次方程式 $8x^3-4x^2-4x+1 = 0$ が得られた.
- (4)
- $a^{-1} = b^{-1}+c^{-1}$ を示すには, $bc = ca+ab$ を示せばよい. $ab-bc+ca$ に $[1],$ $[2]$ を代入して整理すると, $[5]$ から \[\begin{aligned} ab-bc+ca &= -a^2(8\cos ^3\theta -4\cos ^2\theta -4\cos\theta +1) \\ &= 0 \end{aligned}\] となり, 求める結果が得られる.
別解
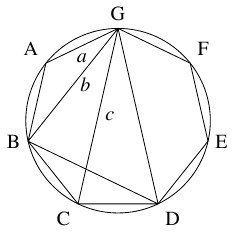
- (4)
- 四角形 $\mathrm{BCDG}$ は円に内接するから, トレミーの定理により,
\[\mathrm{BD}\cdot\mathrm{CG} = \mathrm{BC}\cdot\mathrm{DG}+\mathrm{CD}\cdot\mathrm{GB}\]
つまり
\[ bc = ac+ab\]
が成り立つ.
両辺を $abc$ で割ると, 求める結果が得られる.
参考
正七角形の $1$ 辺の長さ $a$ と対角線の長さ $b,$ $c$ に関する関係式 $a^{-1} = b^{-1}+c^{-1}$ は「正七角形調和」と呼ばれる.
問題《$\cos (\pi /9)$ を解にもつ $3$ 次方程式》
- (1)
- $\cos\dfrac{\pi}{9}$ を解にもつ整数係数方程式を $1$ つ求めよ.
- (2)
- $\cos\dfrac{\pi}{9}$ は無理数であることを示せ. ただし, 整数係数 $n$ 次方程式 $a_nx^n+\cdots +a_1x+a_0 = 0$ $(a_0a_n \neq 0)$ の有理数解 $\alpha$ が $\alpha = \dfrac{p}{q}$ ($p$: $a_0$ の約数, $q$: $a_n$ の約数) の形に表されるという「有理根定理」(こちらを参照) は, 証明なしに使ってよい.
(参考: $2017$ 金沢大)
解答例
- (1)
- $3$ 倍角の公式 $\cos 3\theta = 4\cos ^3\theta -3\cos\theta$ に $\theta = \dfrac{\pi}{9}$ を代入すると \[ 4\cos ^3\frac{\pi}{9}-3\cos\frac{\pi}{9} = \cos\frac{\pi}{3} = \frac{1}{2}\] つまり \[ 8\cos ^3\frac{\pi}{9}-6\cos\frac{\pi}{9}-1 = 0\] となるから, $\cos\dfrac{\pi}{9}$ を解にもつ整数係数方程式の $1$ つは \[ 8x^3-6x-1 = 0 \quad \cdots [1]\] である.
- (2)
- 「有理根定理」により, $[1]$ の有理数解の候補は, \[ x = \pm 1,\ \pm\frac{1}{2},\ \pm\frac{1}{4},\ \pm\frac{1}{8}\] に限る. $[1]$ の左辺にこれらの値を代入しても $0$ にならないから, $[1]$ は有理数解をもたない. 一方, $\cos\dfrac{\pi}{9}$ は $[1]$ の解であるから, $\cos\dfrac{\pi}{9}$ は無理数である.
参考
- 与えられた角に対して $3$ 分の $1$ の大きさの角を (目盛りのない) 定規とコンパスのみで作図できるかという問題を「角の三等分問題」(angle trisection problem) と呼ぶ. $19$ 世紀半ば, P・ヴァンツェルは, 一般的にはこのような作図が不可能であること (このような作図ができない角の存在) を証明した.
- 座標平面上の点 $(a,b)$ が定規とコンパスで作図可能であるためには, $a,$ $b$ が有理数から加減乗除または平方根をとる操作を繰り返して表せることが必要十分である. この定理は,「体」の概念 (こちらを参照) を使うと, 簡潔な主張の記述, 証明が可能になる.
- 本問の結果により $8x^3-6x-1 = 0$ の左辺は $1$ 次式で割り切れず, よって $2$ 次以下の多項式の積に因数分解できないから, $\cos\dfrac{\pi}{9}$ は有理数から加減乗除または平方根をとる操作を繰り返して表せない. このことから, $2$ 直線 $y = 0,$ $y = \sqrt 3x$ のなす鋭角 (大きさは $\dfrac{\pi}{3}$) の三等分線は定規とコンパスのみで作図できないことがわかる.
- $\sin\dfrac{\pi}{18}$ が $8x^3-6x+1 = 0$ の解であり, 無理数であることからも, 三等分線が定規とコンパスで作図できない角の存在が示される.
$n$ 倍角の公式
問題《チェビシェフ多項式の存在》
$n$ を正の整数とする.
すべての実数 $\theta$ に対して
\[\begin{cases}
\cos n\theta = T_n(\cos\theta ) & \cdots [\mathrm A], \\
\sin n\theta = \sin\theta\,U_{n-1}(\cos\theta ) & \cdots [\mathrm B]
\end{cases}\]
を満たす整数係数の $n$ 次多項式 $T_n(x),$ $n-1$ 次多項式 $U_{n-1}(x)$ が存在することを示せ.
(参考: $1996$ 京都大)
解答例
より強い命題 “ $[\mathrm A],$ $[\mathrm B]$ を満たし, 最高次の係数が正である整数係数の $n$ 次多項式 $T_n(x),$ $n-1$ 次多項式 $U_{n-1}(x)$ が存在する ” $\cdots [\mathrm P]$ を数学的帰納法で示す.
- (i)
- $n = 1$ のとき. $T_1(x) = x,$ $U_0(x) = 1$ は $[\mathrm P]$ の条件を満たす.
- (ii)
- $n = k$ ($k$: 正の整数) のとき $[\mathrm P]$ が成り立つとする. このとき, \[\begin{aligned} \cos (k+1)\theta &= \cos (k\theta +\theta ) \\ &= \cos k\theta\cos\theta -\sin k\theta\sin\theta \\ &= \cos\theta\,T_k(\cos\theta )-\sin ^2\theta\,U_{k-1}(\cos\theta ) \\ &= \cos\theta\,T_k(\cos\theta )+(\cos ^2\theta -1)U_{k-1}(\cos\theta ), \\ \sin (k+1)\theta &= \sin (k\theta +\theta ) \\ &= \sin k\theta\cos\theta +\cos k\theta\sin\theta \\ &= \sin\theta\cos\theta\,U_{k-1}(\cos\theta )+\sin\theta\,T_k(\cos\theta ) \\ &= \sin\theta\{\cos\theta\,U_{k-1}(\cos\theta )+T_k(\cos\theta )\} \end{aligned}\] から, \[\begin{aligned} T_{k+1}(x) &= xT_k(x)+(x^2-1)U_{k-1}(x), \\ U_k(x) &= xU_{k-1}(x)+T_k(x) \end{aligned}\] は $n = k+1$ の場合の $[\text A]$ と $[\text B]$ を満たす. また, $T_k(x)$ と $U_{k-1}(x)$ は整数係数であるから, $T_{k+1}(x)$ と $U_k(x)$ も整数係数である. さらに, $T_k(x)$ の $x^k$ の係数と $U_{k-1}(x)$ の $x^{k-1}$ の係数は正であるから, $T_{k+1}(x)$ の $x^{k+1}$ の係数と $U_k(x)$ の $x^k$ の係数は正であり, $T_{k+1}(x)$ は $k+1$ 次で $U_k(x)$ は $k$ 次である. よって, $T_{k+1}(x),$ $U_k(x)$ は $[\mathrm P]$ の条件を満たす.
別解 1
$c = \cos\theta,$ $s = \sin\theta$ とおく.
ド・モアブルの定理と二項定理により,
\[\begin{aligned}
&\cos n\theta +i\sin n\theta = (c+si)^n \\
&= \sum_{k = 0}^n{}_n\mathrm C_kc^{n-k}(si)^k \\
&= \sum_{0 \leqq k \leqq n,\,k:\text{偶数}}{}_n\mathrm C_kc^{n-k}(si)^k \\
&\qquad +\sum_{0 \leqq k \leqq n,\,k:\text{奇数}}{}_n\mathrm C_kc^{n-k}(si)^k \\
&= \sum_{0 \leqq k \leqq n,\,k:\text{偶数}}{}_n\mathrm C_kc^{n-k}(-s^2)^{\frac{k}{2}} \\
&\qquad +\sum_{0 \leqq k \leqq n,\,k:\text{奇数}}{}_n\mathrm C_kc^{n-k}(-s^2)^{\frac{k-1}{2}}(si) \\
&= \sum_{0 \leqq k \leqq n,\,k:\text{偶数}}{}_n\mathrm C_kc^{n-k}(c^2-1)^{\frac{k}{2}} \\
&\qquad +is\sum_{0 \leqq k \leqq n,\,k:\text{奇数}}{}_n\mathrm C_kc^{n-k}(c^2-1)^{\frac{k-1}{2}}
\end{aligned}\]
が成り立つ.
ここで, 右辺の和の記号は, それぞれ $0 \leqq k \leqq n$ なるすべての偶数, 奇数 $k$ にわたる和を表す.
両辺の実部, 虚部をそれぞれ比較すると,
\[\begin{aligned}
\cos n\theta &= \sum_{0 \leqq k \leqq n,\,k:\text{偶数}}{}_n\mathrm C_kc^{n-k}(c^2-1)^{\frac{k}{2}}, \\
\sin n\theta &= s\sum_{0 \leqq k \leqq n,\,k:\text{奇数}}{}_n\mathrm C_kc^{n-k}(c^2-1)^{\frac{k-1}{2}}
\end{aligned}\]
となる.
よって, 多項式
\[\begin{aligned}
T_n(x) &= \sum_{0 \leqq k \leqq n,\,k:\text{偶数}}{}_n\mathrm C_kx^{n-k}(x^2-1)^{\frac{k}{2}},\\
U_{n-1}(x) &= \sum_{0 \leqq k \leqq n,\,k:\text{奇数}}{}_n\mathrm C_kx^{n-k}(x^2-1)^{\frac{k-1}{2}}
\end{aligned}\]
は $\cos n\theta = T_n(\cos\theta ),$ $\sin n\theta = \sin\theta\,U_{n-1}(\cos\theta )$ を満たす.
$T_n(x),$ $U_{n-1}(x)$ の最高次の項はそれぞれ
\[\sum_{0 \leqq k \leqq n,\,k:\text{偶数}}{}_n\mathrm C_kx^n, \quad \sum_{0 \leqq k \leqq n,\,k:\text{奇数}}{}_n\mathrm C_kx^{n-1}\]
に等しいから, $T_n(x)$ は $n$ 次, $U_{n-1}(x)$ は $n-1$ 次の整数係数多項式である.
別解 2
余弦, 正弦の加法定理により
\[\begin{aligned}
\cos (n+2)\theta &= \cos (n+1)\theta\cos\theta -\sin (n+1)\theta\sin\theta, \\
\cos n\theta &= \cos (n+1)\theta\cos\theta +\sin (n+1)\theta\sin\theta, \\
\sin (n+2)\theta &= \sin (n+1)\theta\cos\theta +\cos (n+1)\theta\sin\theta, \\
\sin n\theta &= \sin (n+1)\theta\cos\theta -\cos (n+1)\theta\sin\theta
\end{aligned}\]
であるから,
\[\begin{aligned}
\cos (n+2)\theta &= 2\cos (n+1)\theta\cos\theta -\cos n\theta, \\
\sin (n+2)\theta &= 2\sin (n+1)\theta\cos\theta -\sin n\theta
\end{aligned}\]
が成り立つ.
そこで, 初期条件 $T_1(x) = x,$ $T_2(x) = 2x^2-1,$ $U_0(x) = 1,$ $U_1(x) = 2x$ と漸化式 $T_{n+2}(x) = 2xT_{n+1}(x)-T_n(x),$ $U_{n+1}(x) = 2xU_n(x)-U_{n-1}(x)$ によって $n$ 次多項式 $T_n(x),$ $n-1$ 次多項式 $U_{n-1}(x)$ を順次定めると,
$[\mathrm A],$ $[\mathrm B]$ を満たす整数係数多項式が得られる.
参考
- 各正の整数 $n$ に対し, $\cos n\theta$ はある $n$ 次多項式 $T_n(x)$ を用いて $\cos n\theta = T_n(\cos\theta )$ と表すことができる. $\cos n\theta$ とは違い, $\sin n\theta$ は $\cos\theta,$ $\sin\theta$ の一方のみの多項式として表せるとは限らないが, ある多項式 $U_{n-1}(x)$ を用いて $\sin n\theta = \sin\theta\,U_{n-1}(\cos\theta )$ と表すことができる. $T_n(x),$ $U_{n-1}(x)$ は, それぞれ「第一種チェビシェフ多項式」,「第二種チェビシェフ多項式」と呼ばれ, あわせて「チェビシェフ多項式」(Chebyshev polynomial) と呼ばれる. これを次数の低い順に書き出していくと, \[\begin{aligned} T_1(x) &= x, & U_1(x) &= 2x, \\ T_2(x) &= 2x^2-1, & U_2(x) &= 4x^2-1, \\ T_3(x) &= 4x^3-3x, & U_3(x) &= 8x^3-4x, \\ T_4(x) &= 8x^4-8x^2+1, & U_4(x) &= 16x^4-12x^2+1, \\ T_5(x) &= 16x^5-20x^3+5x, & U_5(x) &= 32x^5-32x^3+6x, \\ \vdots\quad& & \vdots\quad& \end{aligned}\] のようになる.
- $T_n(x),$ $U_n(x)$ の最高次の係数はそれぞれ $2^{n-1},$ $2^n$ である. また, $T_n(x),$ $U_n(x)$ の定数項は $n$ が偶数 $2k$ のとき $(-1)^k,$ $n$ が奇数のとき $0$ である.
(修正: $U_n(x)$ の添え字を一般的な記法に変更, $2022/05/03$)
問題《チェビシェフ多項式の性質》
$T_0(x) = 1,$ $T_1(x) = x$ と漸化式
\[ T_{n+2}(x) = 2xT_{n+1}(x)-T_n(x)\]
により多項式 $T_n(x)$ $(n \geqq 0)$ を定める.
- (1)
- すべての非負整数 $n,$ 実数 $\theta$ に対して \[ T_n(\cos\theta ) = \cos n\theta \quad \cdots [\text P]\] が成り立つことを数学的帰納法で示せ.
- (2)
- $m$ を正の整数とする. $T_m(x) = 0$ の実数解を余弦の値で表せ.
- (3)
- $T_n(x)$ を $x$ の関数とみなすとき, $n$ が偶数のとき $T_n(x)$ は偶関数であり, $n$ が奇数のとき $T_n(x)$ は奇関数であることを示せ.
- (4)
- $n \geqq 2$ で, $n$ の正の約数 $m$ について $\dfrac{n}{m}$ が奇数であるとする. このとき, $T_m(x)$ は $T_n(x)$ を割り切ることを示せ.
(参考: $2002$ 九州大)
解答例
- (1)
- (i)
- $n = 0,$ $1$ のとき. $T_0(\cos\theta ) = 1 = \cos (0\cdot\theta ),$ $T_1(\cos\theta ) = \cos (1\cdot\theta )$ から, $[\text P]$ が成り立つ.
- (ii)
- $n = k,$ $k+1$ ($k$: 非負整数) のとき $[\text P]$ が成り立つとする. このとき, 三角関数の積和の公式により \[\begin{aligned} T_{k+2}(\cos\theta ) &= 2\cos\theta T_{k+1}(\cos\theta )-T_k(\cos\theta ) \\ &= 2\cos (k+1)\theta\cos\theta -\cos k\theta \\ &= \cos (k+2)\theta +\cos k\theta -\cos k\theta \\ &= \cos (k+2)\theta \end{aligned}\] となり, $n = k+2$ のとき $[\text P]$ が成り立つ.
- (2)
- $x = \cos\theta$ $(0 \leqq \theta \leqq \pi )$ が $T_m(x) = 0$ の解であるとすると, (1) の結果により $\cos m\theta = 0$ となり, \[ m\theta = (2k-1)\frac{\pi}{2}\] つまり \[\theta = \frac{2k-1}{m}\cdot\frac{\pi}{2} \quad (k = 1,\ \cdots,\ m)\] となるので, $x$ は \[ x = \cos\left(\frac{2k-1}{m}\cdot\frac{\pi}{2}\right) \quad (k = 1,\ \cdots,\ m)\] と表される. $m$ 次方程式は $m$ 個以下しか解をもたないから, これが解のすべてである.
- (3)
- 等式
\[ T_n(-x) = (-1)^nT_n(x) \quad \cdots [\text Q]\]
を示せばよい.
- (i)
- $n = 0,$ $1$ のとき. $T_0(-x) = 1 = T_0(x),$ $T_1(-x) = -x = -T_1(x)$ から, $[\text Q]$ が成り立つ.
- (ii)
- $n = k,$ $k+1$ ($k$: 非負整数) のとき $[\text Q]$ が成り立つとする. このとき, \[\begin{aligned} T_{k+2}(-x) &= 2(-x)T_{k+1}(-x)-T_k(-x) \\ &= -2x\cdot (-1)^{k+1}T_{k+1}(x)-(-1)^kT_k(x) \\ &= (-1)^{k+2}\{ 2xT_{k+1}(x)-T_k(x)\} \\ &= (-1)^{k+2}T_{k+2}(x) \end{aligned}\] となり, $n = k+2$ のとき $[\text Q]$ が成り立つ.
- (4)
- $q = \dfrac{n}{m}$ とおき, $1 \leqq k \leqq m$ なる各整数 $k$ に対して $\theta _k = \dfrac{2k-1}{m}\cdot\dfrac{\pi}{2}$ とおく. (1) と, (3) で示した通り $T_q(x)$ が奇関数であることから, \[\begin{aligned} T_n(\cos\theta _k) &= \cos n\theta _k = \cos q(m\theta _k) = T_q(\cos m\theta _k) \\ &= T_q(T_m(\cos\theta _k)) = T_q(0) = 0 \end{aligned}\] である. よって, 因数定理により $x-\cos\theta _k$ $(1 \leqq k \leqq m)$ は $T_n(x)$ を割り切る. ゆえに, $T_m(x)$ は $T_n(x)$ を割り切る.
参考
「チェビシェフ多項式」は初期条件 $T_0(x) = 1,$ $T_1(x) = x,$ $U_0(x) = 1,$ $U_1(x) = 2x$ と漸化式 $T_{n+2}(x) = 2xT_{n+1}(x)-T_n(x),$ $U_{n+2}(x) = 2xU_{n+1}(x)-U_n(x)$ によって定まる.
本問の結果の他に, 次のような「チェビシェフ多項式」の性質がよく知られている.
- $T_n{}'(x) = nU_{n-1}(x)$ が成り立つ. 実際, $[\mathrm A]$ の両辺を $\theta$ で微分すると, 合成関数の微分法により, \[ -n\sin n\theta = -\sin\theta\,T_n{}'(\cos\theta )\] となる. $[\mathrm B]$ を代入すると, \[ \sin\theta\,T_n{}'(\cos\theta ) = n\sin\theta\,U_{n-1}(\cos\theta )\] を得る. よって, $\sin\theta \neq 0$ なるすべての実数 $\theta$ に対し, したがって $\cos\theta$ の相異なる $n$ 個の値に対して \[ T_n{}'(\cos\theta ) = nU_{n-1}(\cos\theta )\] が成り立つ. $T_n{}'(x)$ と $nU_{n-1}(x)$ は $n-1$ 次多項式であるから,「一致の定理」により, $T_n{}'(x) = nU_{n-1}(x)$ が成り立つ.
- $T_n(x) = 0$ は区間 $(-1,1)$ において $n$ 個の実数解 \[ x = \cos\frac{2k-1}{2n}\pi \quad (k = 1,\ \cdots,\ n)\] をもつ. また, $T_n(x)$ は, 区間 $[-1,1]$ 上の $n+1$ 個の点 \[ x = \cos\frac{k}{n}\pi \quad (k = 0,\ 1,\ \cdots,\ n)\] において極値をとる.
- 最高次の項が $x^n$ である $n$ 次関数 $f(x)$ の $-1 \leqq x \leqq 1$ における最大値 $M$ について $M \geqq \dfrac{1}{2^{n-1}}$ が成り立ち, 等号成立は $f(x) = \dfrac{1}{2^{n-1}}T_n(x)$ の場合に限る.
問題《ニーヴェンの定理》
次のことを示せ.
- (1)
- $n$ を正の整数とする. すべての実数 $\theta$ に対して $f_n(2\cos\theta ) = 2\cos n\theta$ を満たし, 最高次の係数が $1$ である整数係数の $n$ 次多項式 $f_n(x)$ が存在する.
- (2)
- 最高次の係数が $1$ の整数係数多項式 $\varphi (x)$ に対して, $\varphi (x) = 0$ が有理数解 $\alpha$ をもつならば, $\alpha$ は整数である.
- (3)
- 鋭角 $\theta$ に対して, $\cos\theta,$ $\dfrac{\theta}{\pi}$ が有理数になるのは, $\theta = \dfrac{\pi}{3}$ のときに限る.
- (4)
- 鋭角 $\theta$ に対して, $\sin\theta,$ $\dfrac{\theta}{\pi}$ が有理数になるのは, $\theta = \dfrac{\pi}{6}$ のときに限る.
- (5)
- 鋭角 $\theta$ に対して, $\tan\theta,$ $\dfrac{\theta}{\pi}$ が有理数になるのは, $\theta = \dfrac{\pi}{4}$ のときに限る. (ヒント: $\cos 2\theta = \dfrac{1-\tan ^2\theta}{1+\tan ^2\theta}$ を使う.)
解答例
- (1)
- $(n+2)\theta = (n+1)\theta +\theta,$ $n\theta = (n+1)\theta -\theta$ から, 加法定理により,
\[\begin{aligned}
\cos (n+2)\theta &= \cos (n+1)\theta\cos\theta -\sin (n+1)\theta\sin\theta, \\
\cos n\theta &= \cos (n+1)\theta\cos\theta +\sin (n+1)\theta\sin\theta
\end{aligned}\]
が成り立つ.
よって,
\[\cos (n+2)\theta = 2\cos (n+1)\theta\cos\theta -\cos n\theta \quad \cdots [1]\]
が成り立つ.
- (i)
- $n = 1,$ $2$ のとき. 多項式 $f_1(x) = x,$ $f_2(x) = x^2-2$ が条件を満たす.
- (ii)
- $n = k,$ $k+1$ ($k$: 正の整数) のとき $f_n(x)$ の存在を仮定する. このとき, $[1]$ から, 多項式 $f_{k+2}(x) = xf_{k+1}(x)-f_k(x)$ が \[\begin{aligned} f_{k+2}(2\cos\theta ) &= 2\cos\theta f_{k+1}(2\cos\theta )-f_k(2\cos\theta ) \\ &= 2\cos\theta\cdot 2\cos (k+1)\theta -2\cos k\theta \\ &= 2\cos (k+2)\theta \end{aligned}\] を満たす. $f_k(x),$ $f_{k+1}(x)$ はそれぞれ最高次の係数が $1$ の整数係数の $k$ 次多項式, $k+1$ 次多項式であるから, $f_{k+2}(x)$ は最高次の係数が $1$ の整数係数の $k+2$ 次多項式である.
- (2)
- 整数係数方程式
\[ x^n+a_{n-1}x^{n-1}+\cdots +a_0 = 0\]
が有理数解 $\alpha$ をもつとする.
$\alpha$ は互いに素な整数 $p,$ $q$ $(q > 0)$ を用いて $\alpha = \dfrac{p}{q}$ と表せる.
このとき,
\[\frac{p^n}{q^n}+a_{n-1}\frac{p^{n-1}}{q^{n-1}}+\cdots +a_0 = 0\]
となるから, 両辺に $q^n\,(> 0)$ を掛けると
\[\begin{aligned}
&p^n+a_{n-1}p^{n-1}q+\cdots +a_0q^n = 0 \\
&p^n = -q(a_{n-1}p^{n-1}+\cdots +a_0q^{n-1})
\end{aligned}\]
となる.
よって, $p^n$ は $q$ の倍数である.
仮に $q > 1$ であるとすると, $q$ の素因数 $l$ に対して, $p^n$ は $l$ の倍数, したがって $p$ は $l$ の倍数になり, $p,$ $q$ が互いに素であることに反する.
ゆえに, $q = 1$ であり, $\alpha$ は整数である. - (3)
- $\theta$ を $\cos\theta,$ $\dfrac{\theta}{\pi}$ が有理数であるような鋭角とする. このとき, ある正の整数 $m,$ $n$ について, $\dfrac{\theta}{\pi} = \dfrac{m}{n}$ となり, \[ f_n(2\cos\theta ) = 2\cos n\theta = 2\cos m\pi = \pm 2\] となる. $\varphi (x) = f_n(x)\mp 2$ とおく (複号同順). $\alpha = 2\cos\theta$ は $\varphi (x) = 0$ の有理数解であり, $\varphi (x)$ は最高次の係数が $1$ の整数係数多項式であるから, (2) を適用すると, $\alpha$ は整数であることがわかる. $\theta$ が鋭角であることから $0 < 2\cos\theta < 2$ であるので, $2\cos\theta = 1$ つまり $\theta = \dfrac{\pi}{3}$ である.
- (4)
- 鋭角 $\theta$ に対して $\theta ' = \dfrac{\pi}{2}-\theta$ とおく. このとき, $\theta'$ も鋭角であり, $\sin\theta = \cos\theta '$ であるから, $\sin\theta,$ $\dfrac{\theta}{\pi}$ が有理数であるのは, $\cos\theta ',$ $\dfrac{\theta'}{\pi}$ が有理数であるときに限り, それは (3) により $\theta' = \dfrac{\pi}{3}$ つまり $\theta = \dfrac{\pi}{6}$ のときに限る.
- (5)
- $\theta$ を $\tan\theta,$ $\dfrac{\theta}{\pi}$ が有理数であるような鋭角とする. \[\cos 2\theta = 2\cos ^2\theta -1 = \frac{2}{1+\tan ^2\theta}-1 = \frac{1-\tan ^2\theta}{1+\tan ^2\theta}\] であるから, $\cos 2\theta$ は有理数である. $0 < 2\theta < \pi,$ $\cos (\pi -2\theta ) = -\cos 2\theta$ に注意すると, (3) により $2\theta = \dfrac{\pi}{3},$ $\dfrac{\pi}{2},$ $\dfrac{2\pi}{3}$ つまり $\theta = \dfrac{\pi}{6},$ $\dfrac{\pi}{4},$ $\dfrac{\pi}{3}$ が得られる. このうち, $\tan\theta$ が有理数である $\theta$ の値は $\theta = \dfrac{\pi}{4}$ のみである.
参考
- (3)~(5), 特に (4) の結果は「ニーヴェンの定理」(Niven's theorem) として知られている.
- 「ニーヴェンの定理」を使うと,「格子正多角形」(各頂点の $x$ 座標, $y$ 座標が整数である正多角形) は正方形に限ることが証明できる (詳細は省略).
