極座標
極座標
問題《$2$ 次曲線の焦点を通る弦》
$e,$ $l > 0$ とする.
$2$ 次曲線 $C:r = \dfrac{l}{1+e\cos\theta}$ について, 次のことを示せ.
- (1)
- $C$ の弦 $\mathrm P_1\mathrm P_2$ が焦点 $\mathrm F$ を通るならば, $\dfrac{1}{\mathrm{FP}_1}+\dfrac{1}{\mathrm{FP}_2} = \dfrac{2}{l}$ が成り立つ.
- (2)
- $C$ の焦点 $\mathrm F$ を通る弦 $\mathrm P_1\mathrm P_2,$ $\mathrm P_3\mathrm P_4$ が直交するならば, $\dfrac{1}{\mathrm{FP}_1\cdot\mathrm{FP}_2}+\dfrac{1}{\mathrm{FP}_3\cdot\mathrm{FP}_4} = \dfrac{2-e^2}{l^2}$ が成り立つ.
解答例
点 $\mathrm P_k$ の極座標を $(r_k,\theta _k)$ $(0 \leqq \theta < 2\pi )$ とおく.
このとき, $r_k = \dfrac{l}{1+e\cos\theta _k}$ である.
- (1)
- \[\begin{aligned} \frac{1}{\mathrm{FP}_1}+\frac{1}{\mathrm{FP}_2} &= \frac{1}{r_1}+\frac{1}{r_2} = \frac{1+e\cos\theta _1}{l}+\frac{1+e\cos\theta _2}{l} \\ &= \frac{2+e(\cos\theta _1+\cos\theta _2)}{l} \end{aligned}\] であるから, \[\begin{aligned} \mathrm F \in \mathrm P_1\mathrm P_2 &\iff \theta _2 = \theta _1\pm\pi \\ &\ \ \Longrightarrow \cos\theta _2 = -\cos\theta _1 \\ &\iff \cos\theta _1+\cos\theta _2 = 0 \\ &\iff \frac{2+e(\cos\theta _1+\cos\theta _2)}{l} = \frac{2}{l} \\ &\iff \frac{1}{\mathrm{FP}_1}+\frac{1}{\mathrm{FP}_2} = \frac{2}{l} \end{aligned}\] が成り立つ.
- (2)
- $\mathrm P_1\mathrm P_2,$ $\mathrm P_3\mathrm P_4$ は $\mathrm F$ を通るから $\theta _2 = \theta _1\pm\pi,$ $\theta _4 = \theta _3\pm\pi$ (複号任意) とおけて, \[\begin{aligned} r_2 &= \dfrac{l}{1+e\cos (\theta _1\pm\pi )} = \dfrac{l}{1-e\cos\theta _1}, \\ r_4 &= \dfrac{l}{1+e\cos (\theta _3\pm\pi )} = \dfrac{l}{1-e\cos\theta _3} \end{aligned}\] が成り立つ. よって, \[\begin{aligned} &\frac{1}{\mathrm{FP}_1\cdot\mathrm{FP}_2}+\frac{1}{\mathrm{FP}_3\cdot\mathrm{FP}_4} \\ &= \frac{1}{r_1}\cdot\frac{1}{r_2}+\frac{1}{r_3}\cdot\frac{1}{r_4} \\ &= \frac{1+e\cos\theta _1}{l}\cdot\frac{1-e\cos\theta _1}{l}+\frac{1+e\cos\theta _3}{l}\cdot\frac{1-e\cos\theta _3}{l} \\ &= \frac{1-e^2\cos ^2\theta _1}{l^2}+\frac{1-e^2\cos ^2\theta _3}{l^2} \\ &= \frac{2-e^2(\cos ^2\theta _1+\cos ^2\theta _3)}{l^2} \end{aligned}\] であるから, \[\begin{aligned} &\mathrm P_1\mathrm P_2 \perp \mathrm P_3\mathrm P_4 \\ &\iff \theta _3 = \theta _1\pm\frac{n\pi}{2}\ (n = \pm 1,\ \pm3) \\ &\ \ \Longrightarrow \cos\theta _3 = \pm\sin \theta _1 \\ &\iff \cos ^2\theta _3 = \sin ^2\theta _1 \\ &\iff \cos ^2\theta _3 = 1-\cos ^2\theta _1 \\ &\iff \cos ^2\theta _1+\cos ^2\theta _3 = 1 \\ &\iff \frac{2-e^2(\cos ^2\theta _1+\cos ^2\theta _3)}{l^2} = \dfrac{2-e^2}{l^2} \\ &\iff \frac{1}{\mathrm{FP}_1\cdot\mathrm{FP}_2}+\frac{1}{\mathrm{FP}_3\cdot\mathrm{FP}_4} = \dfrac{2-e^2}{l^2} \end{aligned}\] が成り立つ.
問題《黄金らせん》
$a\,(\neq 1)$ を正の数とし, 極方程式
\[ r = a^\theta\]
で定まる曲線を $C$ とおく.
- (1)
- $\alpha$ を実数, $k$ を正の数とする.
次のことを示せ.
- $C$ を極の周りに角 $\alpha$ だけ回転することは, 極を中心に $a^\alpha$ 倍に拡大することに他ならない.
- $C$ を極を中心に $k$ 倍に拡大することは, 極の周りに角 $\log_ak$ だけ回転することに他ならない.
- $C$ と $C$ 自身は $1:k$ の比 (任意の比) で相似である.
- (2)
- 各整数 $n$ に対して, $C$ の $\dfrac{(n-1)\pi}{2} \leqq \theta \leqq \dfrac{n\pi}{2}$ の部分と $\dfrac{n\pi}{2} \leqq \theta \leqq \dfrac{(n+1)\pi}{2}$ の部分が $1:\dfrac{1+\sqrt 5}{2}$ の比で相似であるとする. このとき, $a$ の値を求めよ.
解答例
- (1)
- \[ a^{\theta +\alpha} = a^\alpha a^\theta\] であるから, $C$ を極の周りに角 $\alpha$ だけ回転することは, 極を中心に $a^\alpha$ 倍に拡大することに他ならない. また, \[ ka^\theta = a^{\log_ak}a^\theta = a^{\theta +\log_ak}\] であるから, $C$ を極を中心に $k$ 倍に拡大することは, 極の周りに角 $\log_ak$ だけ回転することに他ならない. さらに, このことから, $C$ と $C$ 自身は $1:k$ の比 (任意の比) で相似である.
- (2)
- が成り立つから,
$a^{\theta +\frac{\pi}{2}} = \dfrac{1+\sqrt 5}{2}a^\theta$ つまり $a^\theta a^{\frac{\pi}{2}} = \dfrac{1+\sqrt 5}{2}a^\theta$ である.$a^{\frac{\pi}{2}} = \dfrac{1+\sqrt 5}{2}$ つまり $a = \left(\dfrac{1+\sqrt 5}{2}\right) ^{\frac{2}{\pi}}$
参考
- 曲線 $[*]$ は, 「等角らせん」(equiangular spiral), 「対数らせん」(logarithmic spiral), または 「ベルヌーイらせん」(Bernoulli spiral) と呼ばれる (名の由来についてはこちらを参照).
- $a = \left(\dfrac{1+\sqrt 5}{2}\right) ^{\frac{2}{\pi}} = 1.35845\cdots$ を底とする「等角らせん」$r = a^\theta$ は, 「黄金らせん」(golden spiral, 下図の金線) と呼ばれ, 半径が「フィボナッチ数」の四分円をらせん状に並べることで得られる「フィボナッチらせん」(Fibonacci spiral, 下図の黒線) をよく近似する.
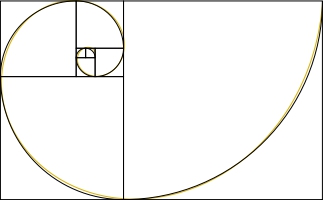
※1: 半径が「フィボナッチ数」の正方形をらせん状に並べることで得られる長方形は有理数比, 「黄金長方形」は無理数比であるため, これらをぴったりと重ねることはできない. この比較図は, $2$ つのらせんを中央付近で合わせるか, 端で合わせるかで, 細かな違いが生じる.
※2: 『高校数学 至極の有名問題 240—文理対応・国公立大~難関大レベル』の表紙は, $1$ 辺が「フィボナッチ数」の正方形をらせん状に並べた模様である.
問題《正葉曲線の対称性》
- (A)
- (1)
- $f(\pi -\theta ) = -f(\theta )$ が成り立つとする. 極方程式 $r = f(\theta )$ で定まる曲線は始線に関して対称であることを示せ.
- (2)
- $n$ を $2$ 以上の偶数とする. 極方程式 $r = \sin n\theta$ で定まる曲線は $n$ 本の直線 $\theta = \dfrac{k\pi}{n}$ ($k$: 整数, $0 \leqq k < n$) により互いに合同な $2n$ 個の図形に分けられることを示せ. また, それら $2n$ 個の部分は互いに極のみを共有することを示せ. さらに, これらのことを参考にして, $n = 2$ のときの概形をかけ.
- (B)
- (1)
- $f(-\theta -\alpha ) = f(\theta -\alpha )$ が成り立つとする. 極方程式 $r = f(\theta )$ で定まる曲線は直線 $\theta = \alpha$ に関して対称であることを示せ.
- (2)
- $n$ を $3$ 以上の奇数とする. 極方程式 $r = \sin n\theta$ で定まる曲線は $n$ 本の半直線 $r \geqq 0,$ $\theta = \dfrac{\pi}{2}+\dfrac{2k\pi}{n}$ ($k$: 整数, $0 \leqq k < n$) に関して対称であることを示せ. また, それらの半直線で分けられた $n$ 個の部分は互いに極のみを共有することを示せ. さらに, これらのことを参考にして, $n = 3$ のときの概形をかけ.
解答例
- (A)
- (1)
- $(f(\pi -\theta ),\pi -\theta ) = (-f(\theta ),\pi -\theta )$ と $(f(\theta ),\theta )$ は始線に関して対称であるから, $r = f(\theta )$ は始線に関して対称である.
- (2)
- $n$ が偶数のとき.
\[\sin n(\pi -\theta ) = \sin (n\pi -n\theta ) = -\sin n\theta\]
であるから, (1) の結果により $r = \sin n\theta$ は始線に関して対称であり, 特に $0 \leqq \theta \leqq \dfrac{\pi}{n}$ の部分 (図では ①) と $\pi -\dfrac{\pi}{n} \leqq \theta \leqq \pi$ の部分 (図では ④) は合同である.
\[\sin n\left(\theta +\frac{2k\pi}{n}\right) = \sin (n\theta +2k\pi) = \sin n\theta\]
であるから, $r = \sin n\theta$ は $0 \leqq \theta \leqq \dfrac{2\pi}{n}$ の部分 (図では ① と ②) を角 $\dfrac{2k\pi}{n}$ ($k$: 整数, $0 \leqq k < n$) だけ回転移動させたもの全体からなる.
さらに, $0 \leqq \theta \leqq \dfrac{\pi}{n}$ の部分 (図では ①) は, $\pi -\dfrac{\pi}{n} \leqq \theta \leqq \pi$ の部分 (図では ④) を回転移動させた $\dfrac{\pi}{n} \leqq \theta \leqq \dfrac{2\pi}{n}$ (図では ②) の部分と合同である.
よって, $r = \sin n\theta$ は $n$ 本の直線 $\theta = \dfrac{k\pi}{n}$ により互いに合同な $2n$ 個の図形に分けられる.
また, \[\sin n(\alpha +\pi ) = \sin n\alpha\] であるから, $r = \sin n\theta$ の $\theta = \alpha$ における点と $\theta = \alpha +\pi$ における点は極に関して対称であり, これと $\cos\theta,$ $\sin\theta,$ $\sin n\theta$ の周期性を合わせると, 上記の $2n$ 個の部分は互いに極のみを共有することがわかる.
さらに, $0 \leqq \theta \leqq 2\pi$ を $2n$ 個の部分 $\dfrac{l\pi}{n} \leqq \theta \leqq \dfrac{(l+1)\pi}{n}$($l$: 整数, $0 \leqq l < 2n$) に分けるとき, $r = \sin n\theta$ の符号は交互に変化し, $\theta = \dfrac{l\pi}{n}+\dfrac{\pi}{2n}$ において円周 $r = 1$ に接する.
よって, $n = 2$ のときの概形は次の通りである.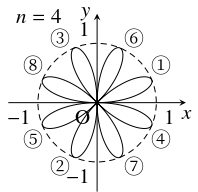
- (B)
- (1)
- $g(\theta ) = f(\theta -\alpha )$ とおく. $(g(-\theta ),-\theta ) = (g(\theta ),-\theta )$ と $(g(\theta ),\theta )$ は対称であるから, $r = g(\theta )$ は $\theta = 0$ に関して対称であり, よって $r = f(\theta )$ は $\theta = \alpha$ に関して対称である.
- (2)
- $n$ が奇数のとき.
\[\begin{aligned}
&\sin n\left(\pm\theta -\frac{\pi}{2}-\frac{2k\pi}{n}\right) = \sin\left(\pm n\theta -\frac{n\pi}{2}-2k\pi\right) \\
&= \sin\left( -\frac{n\pi}{2}\pm n\theta\right) \\
&= \sin\left( -\frac{n\pi}{2}\right)\cos n\theta\pm\cos\left( -\frac{n\pi}{2}\right)\sin n\theta \\
&= -\sin\frac{n\pi}{2}\cos n\theta \quad \text{(複号同順)}
\end{aligned}\]
であるから, (1) の結果により $r = \sin n\theta$ は直線 $\theta = \dfrac{\pi}{2}+\dfrac{2k\pi}{n}$ ($k$: 整数, $0 \leqq k < n$) に関して対称である.
また, $\cos\theta,$ $\sin\theta,$ $\sin n\theta$ の周期性により, 半直線 $r \geqq 0,$ $\theta = \dfrac{\pi}{2}+\dfrac{2k\pi}{n}$ で分けられた $n$ 個の部分は互いに極のみを共有する.
さらに, $0 \leqq \theta \leqq \pi$ を $n$ 個の部分 $\dfrac{k\pi}{n} \leqq \theta \leqq \dfrac{(k+1)\pi}{n}$($k$: 整数, $0 \leqq k < n$) に分けるとき, $r = \sin n\theta$ の符号は交互に変化し, $\theta = \dfrac{k\pi}{n}+\dfrac{\pi}{2n}$ において円周 $r = 1$ に接する.
よって, $n = 3$ のときの概形は次の通りである.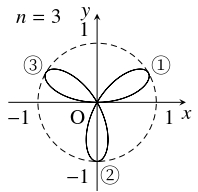
参考
極方程式 $r = \sin n\theta$ で定義された曲線は「正葉曲線」または「バラ曲線」(rose curve) と呼ばれる.
問題《レムニスケートの極方程式》
- (1)
- 直交座標表示で, 平面上の点 $\mathrm A(-1,0),$ $\mathrm B(1,0)$ からの距離の積が $1$ である点 $\mathrm P(x,y)$ の軌跡は, 方程式 $(x^2+y^2)^2 = 2(x^2-y^2)$ で表されることを示せ.
- (2)
- (1) の点 $\mathrm P$ の軌跡を, 極方程式で表せ.
解答例
- (1)
- 定義から \[\begin{aligned} &\mathrm{AP}\cdot\mathrm{BP} = 1 \\ &\iff \mathrm{AP}^2\cdot\mathrm{BQ}^2 = 1 \\ &\iff \{ (x+1)^2+y^2\}\{ (x-1)^2+y^2\} = 1 \\ &\iff (x+1)^2(x-1)^2+\{ (x+1)^2+(x-1)^2\}y^2+y^4 = 1 \\ &\iff (x^2-1)^2+(2x^2+2)y^2+y^4 = 1 \\ &\iff (x^4-2x^2+1)+(2x^2y^2+2y^2)+y^4 = 1 \\ &\iff x^4+2x^2y^2+y^4 = 2x^2-2y^2 \\ &\iff (x^2+y^2)^2 = 2(x^2-y^2) \end{aligned}\] であるので, 点 $\mathrm P$ の軌跡は方程式 $(x^2+y^2)^2 = 2(x^2-y^2)$ で表される.
- (2)
- $x = r\cos\theta,$ $y = r\sin\theta$ とおくと,
\[\begin{aligned}
x^2+y^2 &= r^2(\cos ^2\theta +\sin ^2\theta ) = r^2, \\
x^2-y^2 &= r^2(\cos ^2\theta -\sin ^2\theta ) = r^2\cos 2\theta
\end{aligned}\]
となるから, 点 $\mathrm P$ の軌跡は
と表される.
$r^4 = 2r^2\cos 2\theta$ つまり $r^2 = 2\cos 2\theta$
参考
- 点 $\mathrm P$ の軌跡は「連珠形」または「レムニスケート」(lemniscate) と呼ばれる.
- 「レムニスケート」は, 直角双曲線の接線にその対称の中心から下ろした垂線の足の軌跡としても定まる.
実際, 直角双曲線 $x^2-y^2 = 2$ の点 $(p,q)$ における接線
\[ px-qy = 2 \quad \cdots [1]\]
に原点から下ろした垂線の方程式は
\[ qx+py = 0 \quad \cdots[2]\]
であり, $[1]\times x+[2]\times y,$ $[1]\times (-y)+[2]\times x$ から
\[\begin{aligned}
p(x^2+y^2) &= 2x \\
q(x^2+y^2) &= -2y
\end{aligned}\]
であるので, 両辺を $2$ 乗して辺々を引くと
\[\begin{aligned}
(p^2-q^2)(x^2+y^2)^2 &= 4(x^2-y^2) \\
(x^2+y^2)^2 &= 2(x^2-y^2)
\end{aligned}\]
が得られる.
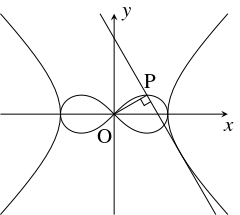
- 「レムニスケート」$r^2 = 2\cos 2\theta$ は \[ x = \frac{\sqrt 2\cos t}{1+\sin ^2t}, \quad y = \frac{\sqrt 2\sin t\cos t}{1+\sin ^2t}\] と媒介変数表示される.
- 「レムニスケート」$(x^2+y^2)^2 = 4a^2xy$ は, 直角双曲線 $xy = \dfrac{a^2}{4}$ 上の動点 $\mathrm P$ を中心とし, 原点を通る円群の「包絡線」として定まる.
