直線
直線の方程式
定理《直線の方程式》
$xy$ 平面上の相異なる $2$ 点 $(x_1,y_1),$ $(x_2,y_2)$ を通る直線の方程式は,
- (i)
- $x_1 \neq x_2$ のとき $y-y_1 = \dfrac{y_2-y_1}{x_2-x_1}(x-x_1)$
- (ii)
- $x_1 = x_2$ のとき $x = x_1$
証明
$(x,y) = (x_1,y_1),$ $(x_2,y_2)$ は上記の $x,$ $y$ の方程式を満たす.
$xy$ 平面では異なる $2$ 点を通る直線はただ $1$ つに定まるから, これが $2$ 点 $(x_1,y_1),$ $(x_2,y_2)$ を通る直線の方程式である.
別証明
$2$ 点 $\mathrm P_1(x_1,y_1),$ $\mathrm P_2(x_2,y_2)$ を通る直線 $l$ の方向ベクトルは $\overrightarrow{\mathrm P_1\mathrm P_2} = (x_2-x_1,y_2-y_1)$ であるから, 平面上の点 $\mathrm P(x,y)$ に対して
\[\begin{aligned}
&\mathrm P \in l \iff \overrightarrow{\mathrm{OP}} = \overrightarrow{\mathrm{OP}_1}+t\overrightarrow{\mathrm P_1\mathrm P_2}\ (t\text{: 実数}) \\
&\iff (x,y) = (x_1,y_1)+t(x_2-x_1,y_2-y_1)\ (t\text{: 実数}) \\
&\iff (x,y) = (x_1\!+\!t(x_2\!-\!x_1),y_1\!+\!t(y_2\!-\!y_1))\ (t\text{: 実数})
\end{aligned}\]
が成り立つ.
最後の式から $t$ を消去すると, 求める方程式が得られる.
問題《$3$ 点が同一直線上にある条件》
平面上の相異なる $3$ 点 $\mathrm P_1(x_1,y_1),$ $\mathrm P_2(x_2,y_2),$ $\mathrm P_3(x_3,y_3)$ が同一直線上にあるための必要十分条件は,
\[ (x_1y_2-y_1x_2)+(x_2y_3-y_2x_3)+(x_3y_1-y_3x_1) = 0\]
であることを示せ.
解答例
- (i)
- $x_1 \neq x_2$ のとき. 直線 $\mathrm P_1\mathrm P_2$ の方程式は \[ y-y_1 = \frac{y_2-y_1}{x_2-x_1}(x-x_1)\] つまり \[ (y_2-y_1)x-(x_2-x_1)y-(x_1y_2-y_1x_2) = 0 \quad \cdots [1]\] である.
- (ii)
- $x_1 = x_2$ のとき. 直線 $\mathrm P_1\mathrm P_2$ の方程式は, $x = x_1$ であり, $[1]$ のように表すこともできる.
| $3$ 点 $\mathrm P_1,$ $\mathrm P_2,$ $\mathrm P_3$ が同一直線上にある |
| $\iff$ 点 $\mathrm P_3$ が直線 $\mathrm P_1\mathrm P_2$ 上にある |
| $\iff$ $(y_2-y_1)x_3-(x_2-x_1)y_3-(x_1y_2-y_1x_2) = 0$ |
| $\iff$ $(x_1y_2\!-\!y_1x_2)+(x_2y_3\!-\!y_2x_3)+(x_3y_1\!-\!y_3x_1) = 0$ |
参考
$\triangle\mathrm P_1\mathrm P_2\mathrm P_3$ の面積は
\[\frac{1}{2}|(x_1y_2-y_1x_2)+(x_2y_3-y_2x_3)+(x_3y_1-y_3x_1)|\]
であるから (こちらを参照), 同一直線上にある $3$ 点 $\mathrm P_1,$ $\mathrm P_2,$ $\mathrm P_3$ は面積 $0$ の三角形をなすと考えると, 上記の条件が得られる.
問題《直線のヘッセ標準形》
- (1)
- $xy$ 平面上の原点 $\mathrm O$ を通らない直線 $l$ の方程式を, $\mathrm O$ から $l$ に下ろした垂線 $\mathrm{OH}$ の長さ $h,$ $\mathrm{OH}$ が $x$ 軸の正方向となす角 $\theta$ を用いて表せ.
- (2)
- 点 $(x_0,y_0)$ と直線 $ax+by+c = 0$ ($a,$ $b,$ $c$: 実数, $(a,b) \neq (0,0)$) の距離 $h$ は $h = \dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$ と表されることを示せ.
注意: 負の角または $180^\circ$ を超える角の三角比を用いる.
解答例
- (1)
- (i)
- $l$ が座標軸と平行でないとき.
垂線 $\mathrm{OH}$ の傾きは $\tan\theta$ である.
よって, $l$ は点 $\mathrm H(h\cos\theta,h\sin\theta )$ を通る傾き $-\dfrac{1}{\tan\theta} = -\dfrac{\cos\theta}{\sin\theta}$ の直線であるから, その方程式は
\[\begin{aligned}
&y-h\sin\theta = -\frac{\cos\theta}{\sin\theta}(x-h\cos\theta ) \\
&x\cos\theta +y\sin\theta = h(\cos ^2\theta +\sin ^2\theta ) \\
&x\cos\theta +y\sin\theta = h \quad \cdots [1]
\end{aligned}\]
と表される.
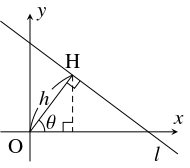
- (ii)
- $l$ が $x$ 軸に平行なとき. $\theta = \pm 90^\circ$ として $[1]$ は $l$ の方程式 $y = \pm h$ を表す.
- (iii)
- $l$ が $y$ 軸に平行なとき. $\theta = 0^\circ,$ $180^\circ$ として $[1]$ は $l$ の方程式 $x = \pm h$ を表す.
- (2)
- 点 $(x_0,y_0)$ と直線 $ax+by+c = 0$ の距離 $h$ は, $x$ 軸方向に $-x_0,$ $y$ 軸方向に $-y_0$ だけ移動した, 原点と直線 $l :a(x+x_0)+b(y+y_0)+c = 0$ の距離に等しい. $\cos\theta = \pm\dfrac{a}{\sqrt{a^2+b^2}},$ $\sin\theta = \pm\dfrac{b}{\sqrt{a^2+b^2}}$ とおくと, $l$ の方程式は \[ x\cos\theta +y\sin\theta = \mp\frac{ax_0+by_0+c}{\sqrt{a^2+b^2}} \quad \cdots [2]\] と変形できる (ただし, 複号同順で, 符号は $[2]$ の右辺が $0$ 以上になるように決める). よって, (1) の結果により \[ h = \mp\frac{ax_0+by_0+c}{\sqrt{a^2+b^2}} = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\] が成り立つ.
参考
$x\cos\theta +y\sin\theta = h$ の形の直線の方程式を「法線標準形」(normal form) または「ヘッセ標準形」(Hesse standard form) と呼ぶ (こちらも参照).
問題《直線と座標軸で囲まれた三角形の計量》
$xy$ 平面において, 原点を $\mathrm O,$ 第 $1$ 象限の点 $(a,b)$ を通る傾きが負の直線と $x$ 軸との交点を $\mathrm P,$ $y$ 軸との交点を $\mathrm Q$ とおく.
- (A)
- $\mathrm{OP}+\mathrm{OQ}$ の最小値を求めよ.
- (B)
- $\triangle\mathrm{OPQ}$ の面積の最小値を求めよ.
解答例
直線の傾きを $-k$ $(k < 0)$ とおく.
点 $(a,b)$ を通る直線の方程式は
\[ y-b = -k(x-a)\]
であるから,
\[\mathrm P\left( a+\frac{b}{k},0\right), \quad \mathrm Q\left( 0,b+ka\right)\]
である.
- (A)
- 相加・相乗平均の不等式により, \[\begin{aligned} \mathrm{OP}+\mathrm{OQ} &= \left( a+\frac{b}{k}\right) +(b+ka) = a+b+\frac{b}{k}+ka \\ &\geqq a+b+2\sqrt{\frac{b}{k}\cdot ka} = a+b+2\sqrt{ab} \\ &= (\sqrt a+\sqrt b)^2 \end{aligned}\] が成り立つ. 等号成立は $\dfrac{b}{k} = ka$ つまり $k = \sqrt{\dfrac{b}{a}}$ のときに限る. よって, $\mathrm{OP}+\mathrm{OQ}$ の最小値は $(\sqrt a+\sqrt b)^2$ である.
- (B)
- 相加・相乗平均の不等式により, \[\begin{aligned} \triangle\mathrm{OPQ} &= \frac{1}{2}\left( a+\frac{b}{k}\right) (b+ka) = \frac{1}{2}\left( 2ab+ka^2+\frac{b^2}{k}\right) \\ &\geqq \frac{1}{2}\left( 2ab+2\sqrt{ka^2\cdot\frac{b^2}{k}}\right) = \frac{1}{2}\left( 2ab+2ab\right) \\ &= 2ab \end{aligned}\] が成り立つ. 等号成立は $ka^2 = \dfrac{b^2}{k}$ つまり $k = \dfrac{b}{a}$ のときに限る. よって, $\triangle\mathrm{OPQ}$ の最小値は $2ab$ である.
直線の平行条件
定理《直線の平行条件》
- (1)
- $2$ 直線 $l_1:y = m_1x+n_1,$ $l_2:y = m_2x+n_2$ ($m_k,$ $n_k$: 定数) に対して, \[ l_1 \,/\!/\, l_2 \iff m_1 = m_2\] が成り立つ.
- (2)
- $2$ 直線 $l_1:a_1x+b_1y+c_1 = 0,$ $l_2:a_2x+b_2y+c_2 = 0$ ($a_k,$ $b_k,$ $c_k$: 定数) に対して, \[ l_1 \,/\!/\, l_2 \iff a_1b_2-b_1a_2 = 0\] が成り立つ.
証明
- (1)
- $l_1,$ $l_2$ と $x$ 軸の正の向きのなす角をそれぞれ $\theta _1,$ $\theta _2$ とおくと, \[\begin{aligned} &l_1 \,/\!/\, l_2 \iff \theta _1 = \theta _2 \\ &\iff \tan\theta _1 = \tan\theta _2 \iff m_1 = m_2 \end{aligned}\] となる.
- (2)
- $b_1b_2 \neq 0$ のとき, (1) の結果により, \[\begin{aligned} &l_1 \,/\!/\, l_2 \iff -\frac{a_1}{b_1} = -\frac{a_2}{b_2} \\ &\iff a_1b_2 = a_2b_1 \iff a_1b_2-a_2b_1 = 0 \end{aligned}\] が成り立つ. また, $b_1b_2 = 0$ のとき,「$b_1 = 0,$ $a_1 \neq 0$」または「$b_2 = 0$ $a_2 \neq 0$」で, $l_1,$ $l_2$ の少なくとも一方は $y$ 軸と平行になるから, \[\begin{aligned} &l_1 \,/\!/\, l_2 \iff b_1 = b_2 = 0 \\ &\iff a_1b_2 = a_2b_1 \iff a_1b_2-a_2b_1 = 0 \end{aligned}\] が成り立つ.
別証明
- (1)
- $l_1,$ $l_2$ の方向ベクトルとしてそれぞれ $\vec{d_1} = (1,m_1),$ $\vec{d_2} = (1,m_2)$ ($x$ 成分は $1$ で等しい) がとれるから, \[\begin{aligned} &l_1 \,/\!/\, l_2 \iff \vec{d_1} \,/\!/\, \vec{d_2} \iff \vec{d_1} = \vec{d_2} \iff m_1 = m_2 \end{aligned}\] が成り立つ.
- (2)
- $l_1,$ $l_2$ の法線ベクトルとしてそれぞれ $\vec{n_1} = (a_1,b_1),$ $\vec{n_2} = (a_2,b_2)$ がとれるから, \[\begin{aligned} l_1 \,/\!/\, l_2 &\iff \vec{n_1} \,/\!/\, \vec{n_2} \iff \vec{n_2} = k\vec{n_2}\ (k\text{: 実数}) \\ &\iff (a_2,b_2) = (ka_1,kb_1)\ (k\text{: 実数}) \\ &\iff a_1b_2-a_2b_1 = 0 \end{aligned}\] が成り立つ.
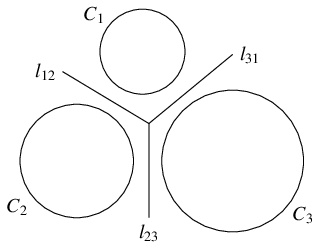
問題《$3$ 円の根心》
$a_k,$ $b_k,$ $c_k$ $(k = 1,\ 2,\ 3)$ を実数として, $x,$ $y$ の多項式
\[\begin{aligned}
f_1(x,y) &= x^2+y^2+a_1x+b_1y+c_1, \\
f_2(x,y) &= x^2+y^2+a_2x+b_2y+c_2, \\
f_3(x,y) &= x^2+y^2+a_3x+b_3y+c_3
\end{aligned}\]
を考える.
方程式 $f_1(x,y)-f_2(x,y) = 0,$ $f_2(x,y)-f_3(x,y) = 0,$ $f_3(x,y)-f_1(x,y) = 0$ がそれぞれ直線 $l_{12},$ $l_{23},$ $l_{31}$ を表すとき, 次のことを示せ.
- (1)
- $l_{12},$ $l_{23}$ が点 $\mathrm P$ で交わるとき, $l_{12},$ $l_{23},$ $l_{31}$ は $1$ 点 $\mathrm P$ で交わる.
- (2)
- $l_{12},$ $l_{23}$ が平行なとき, $l_{12},$ $l_{23},$ $l_{31}$ は互いに平行である.
解答例
- (1)
- $l_{12},$ $l_{23}$ が点 $\mathrm P(x,y)$ で交わるとする. このとき, $f_1(x,y)-f_2(x,y) = 0,$ $f_2(x,y)-f_3(x,y) = 0$ であり, よって \[\begin{aligned} &f_3(x,y)-f_1(x,y) \\ &= -\{ f_1(x,y)-f_2(x,y)\} -\{ f_2(x,y)-f_3(x,y)\} \\ &= -0-0 = 0 \end{aligned}\] が成り立つから, $\mathrm P$ は $l_{31}$ 上にある. ゆえに, $l_{12},$ $l_{23},$ $l_{31}$ は $1$ 点 $\mathrm P$ で交わる.
- (2)
- $l_{12},$ $l_{23},$ $l_{31}$ の方程式はそれぞれ \[\begin{aligned} (a_1-a_2)x+(b_1-b_2)y+c_1-c_2 &= 0, \\ (a_2-a_3)x+(b_2-b_3)y+c_2-c_3 &= 0, \\ (a_3-a_1)x+(b_3-b_1)y+c_3-c_1 &= 0 \end{aligned}\] であるから, \[\begin{aligned} &l_{12} \,/\!/\,l_{23} \\ \iff &(a_1-a_2)(b_2-b_3)-(b_1-b_2)(a_2-a_3) = 0 \\ \iff &a_1b_2-a_1b_3+a_2b_3-a_2b_1+a_3b_1-a_3b_2 = 0 \\ \iff &a_1b_3-a_2b_3+a_2b_1-a_3b_1+a_3b_2-a_1b_2 = 0 \\ \iff &(a_1-a_2)(b_3-b_1)-(b_1-b_2)(a_3-a_1) = 0 \\ \iff &l_{12} \,/\!/\, l_{31} \end{aligned}\] が成り立つ. ゆえに, $l_{12},$ $l_{23}$ が平行なとき, $l_{12},$ $l_{23},$ $l_{31}$ は互いに平行である.
参考
方程式 $f_1(x,y) = 0,$ $f_2(x,y) = 0,$ $f_3(x,y) = 0$ がそれぞれ円周 $C_1,$ $C_2,$ $C_3$ を表すとし, それらのどの $2$ つも中心が異なるとする.
- $l_{12}$ は $C_1,$ $C_2$ の交点を結ぶ直線, 共通接線, または $C_1,$ $C_2$ に向かって長さの等しい接線が引ける点の軌跡であり, $2$ 円 $f_1(x,y) \leqq 0,$ $f_2(x,y) \leqq 0$ の「根軸」(radical axis) と呼ばれる (こちらを参照).
- $3$ 本の「根軸」$l_{12},$ $l_{23},$ $l_{31}$ が $1$ 点で交わるとき, 交点を $3$ 円 $f_1(x,y) \leqq 0,$ $f_2(x,y) \leqq 0,$ $f_3(x,y) \leqq 0$ の「根心」(radical center) と呼ぶ.
- $3$ 円に対して,「根心」を中心とし, $3$ 円に直交する円の存在が知られている.
直線の垂直条件
定理《直線の垂直条件》
- (1)
- $2$ 直線 $l_1:y = m_1x+n_1,$ $l_2:y = m_2x+n_2$ ($m_k,$ $n_k$: 定数) に対して, \[ l_1 \perp l_2 \iff m_1m_2 = -1\] が成り立つ.
- (2)
- $2$ 直線 $l_1:a_1x+b_1y+c_1 = 0,$ $l_2:a_2x+b_2y+c_2 = 0$ ($a_k,$ $b_k,$ $c_k$: 定数) に対して, \[ l_1 \perp l_2 \iff a_1a_2+b_1b_2 = 0\] が成り立つ.
証明
- (1)
- 直線 $l_1,$ $l_2$ と平行な直線 $l_1{}':y = m_1x,$ $l_2{}':y = m_2x$ 上に点 $(1,m_1),$ $(1,m_2)$ をとる. このとき, \[\begin{aligned} &l_1 \perp l_2 \iff l_1{}' \perp l_2{}' \\ &\iff \angle\mathrm P_1\mathrm O\mathrm P_2 \!=\! 90^\circ \iff \mathrm{OP}_1{}^2\!+\!\mathrm{OP}_2{}^2 \!=\! \mathrm P_1\mathrm P_2{}^2 \\ &\iff (1+m_1{}^2)+(1+m_2{}^2) = (m_2-m_1)^2 \\ &\iff 2 = -2m_1m_2 \iff m_1m_2 = -1 \end{aligned}\] が成り立つ.
- (2)
- $b_1b_2 \neq 0$ のとき, (1) の結果により, \[\begin{aligned} &l_1 \perp l_2 \iff \left( -\frac{a_1}{b_1}\right)\left( -\frac{a_2}{b_2}\right) = -1 \\ &\iff a_1a_2 = -b_1b_2 \iff a_1a_2+b_1b_2 = 0 \end{aligned}\] が成り立つ. また, $b_1b_2 = 0$ のとき,「$b_1 = 0,$ $a_1 \neq 0$」または「$b_2 = 0$ $a_2 \neq 0$」で, $l_1,$ $l_2$ の少なくとも一方は $y$ 軸と平行になるから, \[\begin{aligned} &l_1 \perp l_2 \iff b_1 = a_2 = 0\text{ または }a_1 = b_2 = 0 \\ &\iff a_1a_2 = b_1b_2 = 0 \iff a_1a_2+b_1b_2 = 0 \end{aligned}\] が成り立つ.
別証明
- (1)
- $l_1,$ $l_2$ の方向ベクトルとしてそれぞれ $\vec{d_1} = (1,m_1),$ $\vec{d_2} = (1,m_2)$ がとれるから, \[\begin{aligned} &l_1 \perp l_2 \iff \vec{d_1} \perp \vec{d_2} \\ &\iff \vec{d_1}\cdot\vec{d_2} = 0 \iff 1\cdot 1+m_1m_2 = 0 \\ &\iff m_1m_2 = -1 \end{aligned}\] が成り立つ.
- (2)
- $l_1,$ $l_2$ の法線ベクトルとしてそれぞれ $\vec{n_1} = (a_1,b_1),$ $\vec{n_2} = (a_2,b_2)$ がとれるから, \[\begin{aligned} &l_1 \perp l_2 \iff \vec{n_1} \perp \vec{n_2} \\ &\iff \vec{n_1}\cdot\vec{n_2} = 0 \iff a_1a_2+b_1b_2 = 0 \end{aligned}\] が成り立つ.
問題《三角形の垂心》
$\triangle\mathrm{ABC}$ の $3$ 頂点から対辺に下ろした垂線は $1$ 点で交わることを示せ.
解答例
直線 $\mathrm{BC}$ 上に $x$ 軸を, 頂点 $\mathrm A$ から $\mathrm{BC}$ に下ろした垂線上に $y$ 軸を引いて, 座標軸を定める.
このとき, $\mathrm A(0,a),$ $\mathrm B(b,0),$ $\mathrm C(c,0)$ $(a \neq 0,\ b \neq c)$ となる.
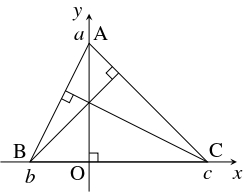

- (i)
- $b = 0$ または $c = 0$ のとき. $3$ 本の垂線は, 直角の頂点 $\mathrm B = \mathrm O$ または $\mathrm C = \mathrm O$ で交わる.
- (ii)
- $b,$ $c \neq 0$ のとき.
直線 $\mathrm{AB}$ の傾きは $-\dfrac{a}{b}$ であるから, 頂点 $\mathrm C$ から $\mathrm{AB}$ に下ろした垂線の方程式は
$y = \dfrac{b}{a}(x-c)$ つまり $y = \dfrac{b}{a}x-\dfrac{bc}{a} \quad \cdots [1]$である. また, 直線 $\mathrm{CA}$ の傾きは $-\dfrac{a}{c}$ であるから, 頂点 $\mathrm B$ から $\mathrm{CA}$ に下ろした垂線の方程式は$y = \dfrac{c}{a}(x-b)$ つまり $y = \dfrac{c}{a}x-\dfrac{bc}{a} \quad \cdots [2]$である. $[1],$ $[2]$ の $y$ 切片はともに $\left( 0,-\dfrac{bc}{a}\right)$ であり, 頂点 $\mathrm A$ から $\mathrm{BC}$ に下ろした垂線は $y$ 軸上にあるから, $3$ 本の垂線は $1$ 点 $\left( 0,-\dfrac{bc}{a}\right)$ で交わる.
参考
三角形の垂心の存在は初等幾何学的に示すこともできるが (こちらを参照), ここでは適当な座標軸をとってこれを示した.
デカルトによって創始された, 座標を用いて方程式で図形を表し, 図形の性質を研究する幾何学は,「解析幾何学」と呼ばれる.
