複素数と図形
複素数平面上の距離
問題《複素数による中線定理の証明》
$\triangle\mathrm{ABC}$ において, 辺 $\mathrm{BC}$ の中点を $\mathrm M$ とおく.
\[\mathrm{AB}^2+\mathrm{AC}^2 = 2(\mathrm{AM}^2+\mathrm{BM}^2) = 2(\mathrm{AM}^2+\mathrm{CM}^2)\]
が成り立つことを, 複素数平面を使って示せ.
解答例
点 $\mathrm M$ を原点として, 実軸, 虚軸を定める.
$\mathrm A(z),$ $\mathrm C(w)$ とおくと, $\mathrm B(-w)$ となるから,
\[\begin{aligned}
\mathrm{AB}^2+\mathrm{AC}^2 &= |z+w|^2+|z-w|^2 \\
&= (z+w)\overline{(z+w)}+(z-w)\overline{(z-w)} \\
&= (z+w)(\bar z+\bar w)+(z-w)(\bar z-\bar w) \\
&= (z\bar z+z\bar w+\bar zw+w\bar w)+(z\bar z-z\bar w-\bar zw+w\bar w) \\
&= 2(|z|^2+|w|^2) \\
&= 2(\mathrm{AM}^2+\mathrm{BM}^2) = 2(\mathrm{AM}^2+\mathrm{CM}^2)
\end{aligned}\]
が成り立つ.
参考
問題《単位円周上の点を結ぶ三角形と四角形》
複素数 $z_1,$ $z_2,$ $z_3,$ $z_4$ は互いに異なり, その絶対値はすべて $1$ であるとする.
次のことを示せ.
- (1)
- $\triangle z_1z_2z_3$ は正三角形である $\iff$ $z_1+z_2+z_3 = 0$ が成り立つ.
- (2)
- 四角形 $z_1z_2z_3z_4$ は長方形である $\iff$ $z_1+z_2+z_3+z_4 = 0$ が成り立つ.
(参考: $2016$ お茶の水女子大)
解答例
- (1)
- 仮定 $|z_1| = |z_2| = |z_3| = 1$ から, $\triangle z_1z_2z_3$ の外心は原点である.
よって,
が成り立つ. なお, 正三角形の重心と外心が一致することは, 明らかである. また, 三角形の重心と外心が一致するとき, 正三角形になることは, 中線が垂直二等分線になり, それによって分けられる直角三角形は合同になって (直角を挟む $2$ 辺が等しい), それらの斜辺の長さが等しくなることからわかる.$\triangle z_1z_2z_3$ は正三角形である $\iff \triangle z_1z_2z_3$ の重心と外心は一致する $\iff \dfrac{z_1+z_2+z_3}{3} = 0$ $\iff z_1+z_2+z_3 = 0$ - (2)
- ($\Longrightarrow$) を示すため, 四角形 $z_1z_2z_3z_4$ が長方形であるとする.
このとき, $\triangle z_1z_2z_3,$ $\triangle z_2z_3z_4$ は $\angle z_1z_2z_3 = 90^\circ,$ $\angle z_2z_3z_4 = 90^\circ$ の直角三角形であるから,
$2$ 本の対角線の中点はそれらの外接円の中心, つまり単位円の中心である原点と一致し,
\[\frac{z_1+z_3}{2} = \frac{z_2+z_4}{2} = 0\]
が成り立つ.
よって,
\[ z_1+z_2+z_3+z_4 = 2\cdot\frac{z_1+z_3}{2}+2\cdot\frac{z_2+z_4}{2} = 0\]
が成り立つ.
($\Longleftarrow$) を示すため, $z_1+z_2+z_3+z_4 = 0$ が成り立つとする. このとき, \[\begin{aligned} z_1+z_2 &= -z_3-z_4 \\ |z_1+z_2| &= |z_3+z_4| \\ |z_1+z_2|^2 &= |z_3+z_4|^2 \\ (z_1+z_2)(\overline{z_1}+\overline{z_2}) &= (z_3+z_4)(\overline{z_3}+\overline{z_4}) \\ |z_1|^2\!+\!z_1\overline{z_2}\!+\!\overline{z_1}z_2\!+\!|z_2|^2 &= |z_3|^2\!+\!z_3\overline{z_4}\!+\!\overline{z_3}z_4\!+\!|z_4|^2 \\ z_1\overline{z_2}+\overline{z_1}z_2 &= z_3\overline{z_4}+\overline{z_3}z_4\ (\because |z_k|^2 \!=\! 1) \end{aligned}\] が成り立つ. 一方, \[\begin{aligned} |z_2-z_1|^2 &= |z_1|^2-z_1\overline{z_2}-\overline{z_1}z_2+|z_2|^2 \\ |z_4-z_3|^2 &= |z_3|^2-z_3\overline{z_4}-\overline{z_3}z_4+|z_4|^2 \end{aligned}\] であるから,$|z_2-z_1|^2 = |z_4-z_3|^2,$ よって $|z_2-z_1| = |z_4-z_3|$が成り立つ. 同様に \[ |z_3-z_2| = |z_1-z_4|\] が成り立ち, 向かい合う辺の長さがそれぞれ等しいから, 四角形 $z_1z_2z_3z_4$ は長方形である.
ゆえに, 四角形 $z_1z_2z_3z_4$ は長方形である $\iff$ $z_1+z_2+z_3+z_4 = 0$ が成り立つ.
問題《三角不等式》
- (1)
- 複素数 $z,$ $w$ に対して \[ |z|+|w| \geqq |z+w|\] が成り立つことを示せ. また, その等号成立条件を求めよ.
- (2)
- 平面上の $3$ 点 $\mathrm P,$ $\mathrm P',$ $\mathrm P''$ に対して \[\mathrm P\mathrm P'+\mathrm P'\mathrm P'' \geqq \mathrm P\mathrm P''\] が成り立つことを示せ. また, その等号成立条件を求めよ.
解答例
- (1)
- 左辺と右辺の $2$ 乗はそれぞれ \[\begin{aligned} (|z|+|w|)^2 &= |z|^2+2|z||w|+|w|^2, \\ |z+w|^2 &= (z+w)\overline{(z+w)} = (z+w)(\bar z+\bar w) \\ &= |z|^2+z\bar w+\bar zw +|w|^2 \end{aligned}\] であるから, 辺々を引くと \[\begin{aligned} (|z|+|w|)^2-|z+w|^2 &= 2|z||w|-(z\bar w+\bar zw) \\ &= 2|z||\bar w|-(z\bar w+\overline{z\bar w}) \\ &= 2\{ |z\bar w|-\mathrm{Re}\,(z\bar w)\} \geqq 0 \end{aligned}\] が得られる. ここで, $\mathrm{Re}\,(z\bar w)$ は $z\bar w$ の実部を表す. 最後の不等号は, すべての実数 $x,$ $y$ に対して成り立つ不等式 \[ x \leqq |x| \leqq \sqrt{x^2+y^2} = |x+yi|\] から従う. よって, $(|z|+|w|)^2 \geqq |z+w|^2,$ $|z|+|w| \geqq 0,$ $|z+w| \geqq 0$ であるから, \[ |z|+|w| \geqq |z+w|\] が成り立つ. 等号成立は, $|z\bar w| = \mathrm{Re}\,(z\bar w),$ つまり $z\bar w$ が $0$ 以上の実数である場合に限る. $z,$ $w \neq 0$ のとき, 偏角を $-\pi$ より大, $\pi$ 以下の範囲で考えると, これは \[\mathrm{arg}\,z\bar w = \mathrm{arg}\,z+\mathrm{arg}\,\bar w = \mathrm{arg}\,z-\mathrm{arg}\,w = 0\] つまり $\mathrm{arg}\,z = \mathrm{arg}\,w$ であることに他ならない.
- (2)
- $3$ 点 $\mathrm P,$ $\mathrm P',$ $\mathrm P''$ に対応する複素数をそれぞれ $z,$ $z',$ $z''$ とおく. このとき, (1)で示したことから \[ |z'-z|+|z''-z'| \geqq |(z'-z)+(z''-z')| = |z''-z|\] が成り立つので, $\mathrm P\mathrm P'+\mathrm P'\mathrm P'' \geqq \mathrm P\mathrm P''$ が得られる. 等号成立は, $z'-z = 0$ または $z''-z' = 0$ または $\mathrm{arg}\,(z'-z) = \mathrm{arg}\,(z''-z')$ である場合, つまり $\mathrm P,$ $\mathrm P',$ $\mathrm P''$ がこの順に同一直線上に並ぶ場合に限る.
別解
- (1)
- (i)
- $z = 0$ または $w = 0$ のとき. $|z|+|w| = |z+w|$ が成り立つ.
- (ii)
- $z,$ $w \neq 0$ のとき. $z = r_1(\cos\theta _1+i\sin\theta _1),$ $w = r_2(\cos\theta _2+i\sin\theta _2)$ ($r_k > 0,$ $\theta _k$: 実数) とおく. このとき, \[\begin{aligned} &(|z|+|w|)^2-|z+w|^2 \\ &= |z|^2+2|z||w|+|w|^2-(z+w)\overline{(z+w)} \\ &= z\bar z+2|z||w|+w\bar w-(z+w)(\bar z+\bar w) \\ &= 2|z||w|-z\bar w-\bar zw \\ &= 2r_1r_2\\ &\quad -r_1(\cos\theta _1+i\sin\theta _1)r_2\{\cos (-\theta _2)+i\sin (-\theta _2)\} \\ &\quad -r_1\{\cos (-\theta _1)+i\sin (-\theta _1)\} r_2(\cos\theta _2+i\sin\theta _2) \\ &= 2r_1r_2\\ &\quad -r_1r_2\{\cos (\theta _1-\theta _2)+i\sin (\theta _1-\theta _2)\} \\ &\quad -r_1r_2\{\cos (\theta _2-\theta _1)+i\sin (\theta _2-\theta _1)\} \\ &= 2r_1r_2-r_1r_2\cdot 2\cos\frac{0}{2}\cos\frac{(\theta _1-\theta _2)-(\theta _2-\theta _1)}{2} \\ &= 2r_1r_2\{ 1-\cos (\theta _1-\theta _2)\} \\ &\geqq 0 \end{aligned}\] であるから, $(|z|+|w|)^2 \geqq |z+w|^2$ つまり $|z|+|w| \geqq |z+w|$ が成り立つ. 等号成立は, $\theta _1-\theta _2$ が $2\pi$ の倍数であるとき, つまり $\mathrm{arg}\,z \equiv \mathrm{arg}\,w \pmod{2\pi}$ である場合に限る.
参考
(2) で示した不等式は「三角不等式」(triangle inequality) と呼ばれる.
回転移動
定理《複素数平面上の点の回転移動》
点 $\alpha$ を中心として点 $\beta$ を角 $\theta$ だけ回転した点が $\gamma$ であるとき,
\[\gamma -\alpha = (\cos\theta +i\sin\theta )(\beta -\alpha )\]
が成り立つ.
証明
平行移動, 拡大・縮小で $2$ 直線のなす角の大きさは変わらないから, $\alpha = 0,$ $|\beta | = |\gamma | = 1$ の場合を示せばよい.
$\alpha = 0,$ $|\beta | = |\gamma | = 1$ の場合は, $\beta$ の偏角を $\varphi$ とすると, $\gamma$ の偏角は $\theta +\varphi$ となるから, \[ (\cos\theta\!+\!i\sin\theta )(\cos\varphi\!+\!i\sin\varphi ) \!=\! \cos (\theta\!+\!\varphi )\!+\!i\sin (\theta\!+\!\varphi )\] により従う.
$\alpha = 0,$ $|\beta | = |\gamma | = 1$ の場合は, $\beta$ の偏角を $\varphi$ とすると, $\gamma$ の偏角は $\theta +\varphi$ となるから, \[ (\cos\theta\!+\!i\sin\theta )(\cos\varphi\!+\!i\sin\varphi ) \!=\! \cos (\theta\!+\!\varphi )\!+\!i\sin (\theta\!+\!\varphi )\] により従う.
問題《複素数平面上の正三角形と正方形の成立条件》
複素平面上の点 $\mathrm A(\alpha ),$ $\mathrm B(\beta ),$ $\mathrm C(\gamma ),$ $\mathrm D(\delta )$ について, $3$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ が三角形 $\mathrm{ABC}$ をなし, $4$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ が四角形 $\mathrm{ABCD}$ をなすとする.
次のことを示せ.
- (A)
- 三角形 $\mathrm{ABC}$ が正三角形であるための必要十分条件は, \[\alpha ^2+\beta ^2+\gamma ^2 = \beta\gamma +\gamma\alpha +\alpha\beta\] である.
- (B)
- 四角形 $\mathrm{ABCD}$ が正方形であるための必要十分条件は, \[\alpha +\gamma = \beta +\delta, \quad (\beta -\alpha )^2+(\delta -\alpha )^2 = 0\] である.
(参考: $2021$ 大阪教育大)
解答例
- (A)
が成り立つ.三角形 $\mathrm{ABC}$ が正三角形 $\iff$ $\overrightarrow{\mathrm{AC}}$ は $\overrightarrow{\mathrm{AB}}$ を $\pm\dfrac{\pi}{3}$ だけ回転したベクトル $\iff$ $\gamma -\alpha = (\beta -\alpha )\left\{\cos\left(\pm\dfrac{\pi}{3}\right) +i\sin\left(\pm\dfrac{\pi}{3}\right)\right\}$ $\iff$ $\gamma -\alpha = (\beta -\alpha )\left(\dfrac{1}{2}\pm\dfrac{\sqrt 3}{2}i\right)$ $\iff$ $\gamma -\dfrac{1}{2}(\alpha +\beta ) = \pm\dfrac{\sqrt 3}{2}(\beta -\alpha )i$ $\iff$ $\left\{\gamma -\dfrac{1}{2}(\alpha +\beta )\right\} ^2 = -\dfrac{3}{4}(\beta -\alpha )^2$ $\iff$ $\alpha ^2 +\beta ^2+\gamma ^2 = \beta\gamma +\gamma\alpha +\alpha\beta$ - (B)
が成り立つ.四角形 $\mathrm{ABCD}$ が正方形 $\iff$ 四角形 $\mathrm{ABCD}$ は平行四辺形, $\mathrm{AB} = \mathrm{AD},$ $\mathrm{AB} \perp \mathrm{AD}$ $\iff$ $\overrightarrow{\mathrm{AC}} = \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AD}},$ $\overrightarrow{\mathrm{AD}}$ は $\overrightarrow{\mathrm{AB}}$ を $\pm\dfrac{\pi}{2}$ だけ回転したベクトル $\iff$ $\gamma -\alpha = (\beta -\alpha )+(\delta -\alpha ),$ $\delta -\alpha = (\beta -\alpha )\left\{\cos\left(\pm\dfrac{\pi}{2}\right) +i\sin\left(\pm\dfrac{\pi}{2}\right)\right\}$ $\iff$ $\alpha +\gamma = \beta +\delta,$ $\delta -\alpha = \pm i(\beta -\alpha )$ $\iff$ $\alpha +\gamma = \beta +\delta,$ $(\delta -\alpha )^2 = -(\beta -\alpha )^2$ $\iff$ $\alpha +\gamma = \beta +\delta,$ $(\beta -\alpha )^2+(\delta -\alpha )^2 = 0$
参考
$3$ 点 $\mathrm A(\alpha ),$ $\mathrm B(\beta ),$ $\mathrm C(\gamma )$ が正三角形をなすためには,
- $\dfrac{\gamma -\alpha}{\beta -\alpha} = \dfrac{\alpha -\beta}{\gamma -\beta}$
- $(\beta -\gamma )^2+(\gamma -\alpha )^2+(\alpha -\beta )^2 = 0$
- $\alpha ^2+\beta ^2+\gamma ^2 = \beta\gamma +\gamma\alpha +\alpha\beta$
- $\alpha +\beta +\gamma = \alpha ^2+\beta ^2+\gamma ^2 = 0$
- $\beta\gamma = \alpha ^2,$ $\gamma\alpha = \beta ^2$
問題《ナポレオンの定理》
複素数平面上に $3$ 点 $\mathrm A(\alpha ),$ $\mathrm B(\beta ),$ $\mathrm C(\gamma )$ が反時計回りに並び, 三角形をなしている.
$\triangle\mathrm{ABC}$ の外側に正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかき,
それらの重心をそれぞれ $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ とおく.
$\zeta = \cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}$ として, 次の問いに答えよ.
- (1)
- $\zeta ^2-\zeta+1$ の値を求めよ.
- (2)
- $\alpha,$ $\beta,$ $\gamma,$ $\zeta$ を用いて, 点 $\mathrm A'',$ $\mathrm B'',$ $\mathrm C''$ に対応する複素数 $\alpha'',$ $\beta'',$ $\gamma''$ を表せ.
- (3)
- $\triangle\mathrm A''\mathrm B''\mathrm C''$ はどのような形の三角形か.
解答例
- (1)
- ド・モアブルの定理により \[\zeta ^3 = \cos\pi +i\sin\pi = -1\] であるから, \[\begin{aligned} \zeta ^3+1 &= 0 \\ (\zeta +1)(\zeta ^2-\zeta +1) &= 0 \end{aligned}\] が成り立つ. $\zeta \neq -1$ つまり $\zeta +1 \neq 0$ であるから, \[\zeta ^2-\zeta +1 = 0 \quad \cdots [1]\] である.
- (2)
- 点 $\mathrm A'(\alpha ')$ は点 $\mathrm C(\gamma )$ を中心として点 $\mathrm B(\beta )$ を $\dfrac{\pi}{3}$ だけ回転した点であるから, \[\begin{aligned} \frac{\alpha '-\gamma}{\beta -\gamma} &= \zeta \\ \alpha '-\gamma &= \zeta (\beta -\gamma ) \\ \alpha ' &= \zeta\beta +(1-\zeta )\gamma \end{aligned}\] である. 点 $\mathrm A''(\alpha '')$ は $\triangle\mathrm A'\mathrm{BC}$ の重心であるから, \[\alpha '' = \frac{\alpha '+\beta +\gamma}{3} = \frac{(1+\zeta )\beta +(2-\zeta )\gamma}{3} \quad \cdots [2]\] である. 同様に, \[\begin{aligned} \beta '' &= \frac{(1+\zeta )\gamma +(2-\zeta )\alpha}{3} \quad \cdots [3], \\ \gamma '' &= \frac{(1+\zeta )\alpha +(2-\zeta )\beta}{3} \quad \cdots [4] \end{aligned}\] である.
- (3)
- $[2]$~$[4]$ から, \[\begin{aligned} &\frac{\gamma ''-\alpha ''}{\beta ''-\alpha ''} = \frac{3\gamma ''-3\alpha ''}{3\beta ''-3\alpha ''} \\ &= \frac{(1+\zeta )\alpha +(2-\zeta )\beta -(1+\zeta )\beta -(2-\zeta )\gamma}{(1+\zeta )\gamma +(2-\zeta )\alpha -(1+\zeta )\beta -(2-\zeta )\gamma} \\ &= \frac{(1+\zeta )\alpha +(1-2\zeta )\beta +(-2+\zeta )\gamma}{(2-\zeta )\alpha +(-1-\zeta )\beta +(-1+2\zeta )\gamma} \end{aligned}\] が成り立つ. ここで, $[1]$ から \[\begin{aligned} \zeta (2-\zeta ) &= 2\zeta -\zeta ^2 = 2\zeta -(\zeta -1) = 1+\zeta, \\ \zeta (-1-\zeta ) &= -\zeta -\zeta ^2 = -\zeta -(\zeta -1) = 1-2\zeta, \\ \zeta (-1+2\zeta ) &= -\zeta +2\zeta ^2 = -\zeta +2(\zeta -1) = -2+\zeta \end{aligned}\] であるので, \[\frac{\gamma ''\!-\!\alpha ''}{\beta ''\!-\!\alpha ''} \!=\! \frac{\zeta (2\!-\!\zeta )\alpha\!+\!\zeta (-1\!-\!\zeta )\beta\!+\!\zeta (-1\!+\!2\zeta )\gamma}{(2\!-\!\zeta )\alpha\!+\!(-1\!-\!\zeta )\beta\!+\!(-1\!+\!2\zeta )\gamma} \!=\! \zeta\] が成り立つ. よって, \[\frac{|\gamma ''-\alpha ''|}{|\beta ''-\alpha ''|} = 1, \quad \mathrm{arg}\,\frac{\gamma ''-\alpha ''}{\beta ''-\alpha ''} = \frac{\pi}{3}\] から \[\mathrm A''\mathrm B'' = \mathrm A''\mathrm C'', \quad \angle\mathrm B''\mathrm A''\mathrm C'' = \frac{\pi}{3}\] が成り立つので, $\triangle\mathrm A''\mathrm B''\mathrm C''$ は正三角形である.
参考
- 本問において $\triangle\mathrm A''\mathrm B''\mathrm C''$ が正三角形になることは, ナポレオンによって発見されたといわれ,「ナポレオンの定理」(Napoleon's theorem) として知られている.
- 余弦定理, 正弦定理, 加法定理による証明については, こちらを参照されたい.
- $\triangle\mathrm{ABC}$ の内側に正三角形 $\mathrm A'\mathrm{BC},$ $\mathrm B'\mathrm{CA},$ $\mathrm C'\mathrm{AB}$ をかいても, それらの重心を結ぶ三角形 $\mathrm A''\mathrm B''\mathrm C''$ は正三角形になることが, 上記と同様に証明できる ($\zeta$ を $\cos\left( -\dfrac{\pi}{3}\right) +i\sin\left( -\dfrac{\pi}{3}\right)$ に置き換える). このことも「ナポレオンの定理」として知られている.
問題《曲線 $\sqrt x+\sqrt y = 1$ の回転移動》
曲線 $C:\sqrt x+\sqrt y = 1$ を原点の周りに角 $\dfrac{\pi}{4}$ だけ回転移動した曲線 $C'$ の方程式を求めよ.
また, その概形を描け.
解答例
曲線 $C$ 上の点 $(x,y)$ を原点の周りに角 $\dfrac{\pi}{4}$ だけ回転した点を $(X,Y)$ とおく.
複素数平面上で考えると, 点 $x+yi$ は点 $X+Yi$ を原点の周りに角 $-\dfrac{\pi}{4}$ だけ回転した点であるから,
\[\begin{aligned}
x+yi &= (X+Yi)\left\{\cos\left( -\frac{\pi}{4}\right)+i\sin\left( -\frac{\pi}{4}\right)\right\} \\
&= \frac{(X+Yi)(1-i)}{\sqrt 2} = \frac{(X+Y)+(-X+Y)i}{\sqrt 2}
\end{aligned}\]
よって $x = \dfrac{X+Y}{\sqrt 2},$ $y = \dfrac{-X+Y}{\sqrt 2}\ \cdots [1]$ である.
また,
\[\begin{aligned}
&\sqrt x+\sqrt y = 1 \\
&\iff (\sqrt x+\sqrt y)^2 = 1,\ x \geqq 0,\ y \geqq 0 \\
&\iff x+2\sqrt{xy}+y = 1,\ x \geqq 0,\ y \geqq 0 \\
&\iff 2\sqrt{xy} = 1-(x+y),\ x \geqq 0,\ y \geqq 0 \\
&\iff 4xy = \{ 1-(x+y)\} ^2,\ x \geqq 0,\ y \geqq 0,\ x+y \leqq 1
\end{aligned}\]
である.
$[1]$ のもとで
\[\begin{aligned}
&4xy = \{ 1-(x+y)\} ^2 \\
&\iff 4\cdot\frac{X+Y}{\sqrt 2}\cdot\frac{-X+Y}{\sqrt 2} = \left( 1-\frac{2Y}{\sqrt 2}\right) ^2 \\
&\iff 2(-X^2+Y^2) = (1-\sqrt 2Y)^2 \\
&\iff -2X^2 = 1-2\sqrt 2Y \\
&\iff Y = \frac{\sqrt 2}{2}X^2+\frac{\sqrt 2}{4}, \\
&\text{“}\,x \geqq 0,\ y \geqq 0,\ x+y \leqq 1\,\text{”} \\
&\iff\text{“}\,X+Y \geqq 0,\ -X+Y \geqq 0,\ \sqrt 2Y \leqq 1\,\text{”} \\
&\iff \text{“}\,-Y \leqq X \leqq Y,\ Y \leqq \frac{\sqrt 2}{2}\,\text{”}
\end{aligned}\]
が成り立つから, 曲線 $C'$ の方程式は
\[ y = \frac{\sqrt 2}{2}x^2+\frac{\sqrt 2}{4} \quad \left( -\frac{\sqrt 2}{2} \leqq x \leqq \frac{\sqrt 2}{2}\right)\]
である.
また, $C'$ の概形は, 次の通りである.
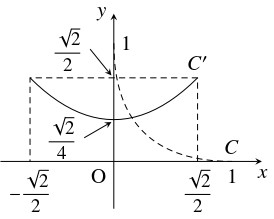

参考
$0 < p < 1$ のとき, $2$ 点 $\mathrm P(x,y),$ $\mathrm P'(x',y')$ に対して $|x'-x|^p+|y'-y|^p$ は $\mathrm P,$ $\mathrm P'$ の「$l^p$ 距離」と呼ばれる.
「$l^p$ 距離」について, 曲線 $|x|^p+|y|^p = 1$ は単位円周のような役割を果たす.
共線・平行・垂直条件
問題《直線の方程式》
$\delta$ を $0$ でない複素数とする.
複素数平面において, 次のことを示せ.
- (A)
- (1)
- 原点と点 $\delta$ を結ぶ直線に平行で点 $\alpha$ を通る直線は方程式 \[\bar\delta (z-\alpha ) -\delta (\bar z-\bar\alpha ) = 0\] で表される.
- (2)
- 原点と点 $\delta$ を結ぶ直線に垂直で点 $\alpha$ を通る直線は方程式 \[\bar\delta (z-\alpha ) +\delta (\bar z-\bar\alpha ) = 0\] で表される.
- (B)
- 相異なる $2$ 点 $\mathrm A,$ $\mathrm B$ を通る直線は \[ (\bar\beta -\bar\alpha )z-(\beta -\alpha )\bar z+\bar\alpha\beta -\alpha\bar\beta = 0\] で表される.
解答例
- (A)
- (1)
- 複素数 $z$ に対して,
が成り立つ.点 $z$ が $0,$ $\delta$ を結ぶ直線に平行で点 $\alpha$ を通る直線上にある $\iff$ ある実数 $k$ に対して $z-\alpha = k\delta$ $\iff \dfrac{z-\alpha}{\delta}$ は実数 $\iff \overline{\left(\dfrac{z-\alpha}{\delta}\right)} = \dfrac{z-\alpha}{\delta}$ $\iff \dfrac{\bar z-\bar\alpha}{\bar\delta} = \dfrac{z-\alpha}{\delta}$ $\iff \bar\delta (z-\alpha ) -\delta (\bar z-\bar\alpha ) = 0$ - (2)
- 複素数 $z$ に対して,
が成り立つ.点 $z$ が $0,$ $\delta$ を結ぶ直線に垂直で点 $\alpha$ を通る直線上にある $\iff \mathrm{arg}\,\dfrac{z-\alpha}{\delta} \equiv \pm\dfrac{\pi}{2} \pmod{2\pi},$ または $z = \alpha$ $\iff \dfrac{z-\alpha}{\delta}$ は純虚数, または $z = \alpha$ $\iff \overline{\left(\dfrac{z-\alpha}{\delta}\right)} = -\dfrac{z-\alpha}{\delta}$ $\iff \dfrac{\bar z-\bar\alpha}{\bar\delta} = -\dfrac{z-\alpha}{\delta}$ $\iff \bar\delta (z-\alpha ) +\delta (\bar z-\bar\alpha ) = 0$
- (B)
- 複素数 $z$ に対して,
が成り立つ.点 $z$ が $\alpha,$ $\beta$ を通る直線上にある $\iff \overline{\left(\dfrac{z-\alpha}{\beta -\alpha}\right)} = \dfrac{z-\alpha}{\beta -\alpha}$ $\iff \dfrac{\bar z-\bar\alpha}{\bar\beta -\bar\alpha} = \dfrac{z-\alpha}{\beta -\alpha}$ $\iff (\bar\beta -\bar\alpha )z-(\beta -\alpha )\bar z+\bar\alpha\beta -\alpha\bar\beta = 0$
問題《三角形の外心》
複素数平面上の点 $\mathrm O(0),$ $\mathrm A(\alpha ),$ $\mathrm B(\beta )$ が三角形を成すとき,
- (1)
- 線分 $\mathrm{OA}$ の垂直二等分線は方程式 \[\overline\alpha z+\alpha\overline z = |\alpha |^2\] で表されることを示せ.
- (2)
- $\triangle\mathrm{OAB}$ の外心に対応する複素数を $\alpha,$ $\beta$ で表せ.
解答例
- (1)
- 点 $\mathrm P(z)$ について,
が成り立つ.$\mathrm P$ が線分 $\mathrm{OA}$ の垂直二等分線上にある \[\begin{aligned} &\iff \mathrm{OP} = \mathrm{AP} \iff \mathrm{OP}^2 = \mathrm{AP}^2 \\ &\iff |z|^2 = |z-\alpha |^2 \\ &\iff z\overline z = (z-\alpha )\overline{(z-\alpha )} \\ &\iff z\overline z = (z-\alpha )(\overline z-\overline\alpha ) \\ &\iff z\overline z = z\overline z-\overline\alpha z-\alpha\overline z-\alpha\overline\alpha \\ &\iff \overline\alpha z+\alpha\overline z = |\alpha |^2 \quad \cdots [1] \end{aligned}\] - (2)
- 点 $\mathrm P(z)$ が線分 $\mathrm{OB}$ の垂直二等分線上にあるとき, (1) と同様に,
\[\overline\beta z+\beta\overline z = |\beta |^2 \quad \cdots [2]\]
が成り立つ.
$\triangle\mathrm{OAB}$ の外心 $\mathrm P(z)$ は $[1],$ $[2]$ を満たすので, $[1]\times\beta -[2]\times\alpha$ から,
\[ (\overline\alpha\beta -\alpha\overline\beta )z = |\alpha |^2\beta-|\beta |^2\alpha \quad \cdots [3]\]
が得られる.
また,
が成り立つ. ゆえに, $\overline\alpha\beta -\alpha\overline\beta \neq 0$ であるので, $[3]$ から \[ z = \frac{|\alpha |^2\beta-|\beta |^2\alpha}{\overline\alpha\beta -\alpha\overline\beta}\] である.$3$ 点 $\mathrm O,$ $\mathrm A,$ $\mathrm B$ は同一直線上にない $\iff$ $\arg\dfrac{\alpha -0}{\beta -0}$ は $\pi$ の倍数でない $\iff$ $\dfrac{\alpha}{\beta}$ は実数でない $\iff$ $\overline{\left(\dfrac{\alpha}{\beta}\right)} \neq \dfrac{\alpha}{\beta}$ $\iff$ $\dfrac{\overline\alpha}{\overline\beta} \neq \dfrac{\alpha}{\beta}$ $\iff$ $\overline\alpha\beta \neq \alpha\overline\beta$
問題《三角形のオイラー線》
$\mathrm A(\alpha ),$ $\mathrm B(\beta ),$ $\mathrm C(\gamma ),$ $\mathrm D(\delta )$ を複素数平面上の点とする.
次のことを示せ.
- (1)
- 直線 $\mathrm{AB},$ $\mathrm{CD}$ が垂直であることと \[ (\beta -\alpha )(\bar\delta -\bar\gamma )+(\bar\beta -\bar\alpha )(\delta -\gamma ) = 0\] が成り立つことは同値である.
- (2)
- 点 $\mathrm A(\alpha ),$ $\mathrm B(\beta ),$ $\mathrm C(\gamma )$ が単位円周上にあり, 三角形をなすとする.
- ①
- $\bar\alpha = \alpha ^{-1},$ $\bar\beta = \beta ^{-1},$ $\bar\gamma = \gamma ^{-1}$ が成り立つ.
- ②
- $\triangle\mathrm{ABC}$ の垂心が $\mathrm H(\eta )$ であるとき \[\eta = \alpha +\beta +\gamma\] が成り立つ.
- ③
- $3$ 点 $\mathrm O,$ $\mathrm G,$ $\mathrm H$ はこの順に一直線上にあり, \[\mathrm{OG}:\mathrm{GH} = 1:2\] である.
解答例
- (1)
- $\mathrm E(\beta -\alpha ),$ $\mathrm F(\delta -\gamma )$ とおくと, $\mathrm{AB} /\!/ \mathrm{OE},$ $\mathrm{CD} /\!/ \mathrm{OF}$ となるから,
が成り立つ.$\mathrm{AB} \perp \mathrm{CD} \iff \mathrm{OE} \perp \mathrm{OF}$ $\iff \mathrm{arg}\dfrac{\delta -\gamma}{\beta -\alpha} = \dfrac{n\pi}{2}$ ($n$: 奇数) $\iff \dfrac{\delta -\gamma}{\beta -\alpha}$ が純虚数 $\iff \overline{\left(\dfrac{\delta -\gamma}{\beta -\alpha}\right)} = -\dfrac{\delta -\gamma}{\beta -\alpha}$ $\iff \dfrac{\bar\delta -\bar\gamma}{\bar\beta -\bar\alpha} = -\dfrac{\delta -\gamma}{\beta -\alpha}$ $\iff (\beta -\alpha )(\bar\delta -\bar\gamma )+(\bar\beta -\bar\alpha )(\delta -\gamma ) = 0$ - (2)
- ①
- $|\alpha | = 1$ よって $\alpha\bar\alpha = |\alpha |^2 = 1$ であるから, $\bar\alpha = \alpha ^{-1}$ が成り立つ. 同様に, $\bar\beta = \beta ^{-1},$ $\bar\gamma = \gamma ^{-1}$ が成り立つ.
- ②
- $\mathrm{AH} \perp \mathrm{BC}$ であることから, (1) の結果により, \[\begin{aligned} (\eta -\alpha )(\bar\gamma -\bar\beta )+(\bar\eta -\bar\alpha )(\gamma -\beta ) &= 0 \\ (\eta -\alpha )(\gamma ^{-1}-\beta ^{-1})+(\bar\eta -\alpha ^{-1})(\gamma -\beta ) &= 0 \\ \alpha (\eta -\alpha )(\beta -\gamma )+\beta\gamma (\alpha\bar\eta -1)(\gamma -\beta ) &= 0 \\ \alpha (\eta -\alpha )-\beta\gamma (\alpha\bar\eta -1) &= 0 \\ \alpha\eta -\alpha\beta\gamma\bar\eta -\alpha ^2+\beta\gamma &= 0 \end{aligned}\] が成り立つ. $\mathrm{BH} \perp \mathrm{CA}$ であることから, 同様に \[\beta\eta -\alpha\beta\gamma\bar\eta -\beta ^2+\gamma\alpha = 0\] が成り立つ. 辺々を引くと, \[\begin{aligned} (\beta -\alpha )\eta -\beta ^2+\alpha ^2+\gamma\alpha -\beta\gamma &= 0 \\ (\beta -\alpha )\eta -(\beta -\alpha )(\alpha +\beta +\gamma ) &= 0 \end{aligned}\] から \[\eta = \alpha +\beta +\gamma\] が得られる.
- ③
- $\triangle\mathrm{ABC}$ の外心は $\mathrm O(0),$ 重心は $\mathrm G\left(\dfrac{\alpha +\beta +\gamma}{3}\right)$ であり, \[\eta = 3\cdot\frac{\alpha +\beta +\gamma}{3}\] であるから, $3$ 点 $\mathrm O,$ $\mathrm G,$ $\mathrm H$ はこの順に一直線上にあり, $\mathrm{OG}:\mathrm{OH} = 1:3$ つまり $\mathrm{OG}:\mathrm{GH} = 1:2$ である.
参考
三角形において, 外心, 重心, 垂心を通る直線を「オイラー線」(Euler line) と呼ぶ (こちらも参照).
ただし, 正三角形に対しては, 外心, 重心, 垂心が一致するため,「オイラー線」は定義されない.
問題《ウォレス=シムソンの定理》
$\mathrm A(\alpha ),$ $\mathrm B(\beta ),$ $\mathrm C(\gamma ),$ $\mathrm D(\delta )$ を複素数平面上の点とする.
- (1)
- $\mathrm A,$ $\mathrm B,$ $\mathrm C$ が同一直線上にあることと \[ (\beta -\alpha )(\bar\gamma -\bar\alpha )-(\bar\beta -\bar\alpha )(\gamma -\alpha ) = 0\] が成り立つことは同値であることを示せ.
- (2)
- $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ が単位円周上にあるとする. このとき, 直線 $\mathrm{AB},$ $\mathrm{CD}$ が平行であることと \[\alpha\beta -\gamma\delta = 0\] が成り立つことは同値であることを示せ.
- (3)
- 直線 $\mathrm{AB},$ $\mathrm{CD}$ が垂直であることと \[ (\beta -\alpha )(\bar\delta -\bar\gamma )+(\bar\beta -\bar\alpha )(\delta -\gamma ) = 0\] が成り立つことは同値であることを示せ.
- (4)
- $\triangle\mathrm{ABC}$ の外接円の周上の点 $\mathrm P$ から直線 $\mathrm{BC},$ $\mathrm{CA},$ $\mathrm{AB}$ に下ろした垂線の足 $\mathrm A'(\alpha '),$ $\mathrm B'(\beta '),$ $\mathrm C'(\gamma ')$ が同一直線上にあることを示したい.
平行移動, 回転移動, 拡大・縮小により, $\mathrm A,$ $\mathrm B,$ $\mathrm C$ が単位円周上にあり, $\mathrm P(1)$ であるとしても一般性を失わないから, その場合を考える.
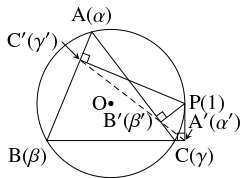
- ①
- $2\alpha' = 1+\beta +\gamma -\beta\gamma,$ $2\beta' = 1+\gamma +\alpha -\gamma\alpha,$ $2\gamma' = 1+\alpha +\beta -\alpha\beta$ であることを示せ.
- ②
- $\mathrm D(-\beta\gamma),$ $\mathrm E(-\gamma\alpha ),$ $\mathrm F(-\alpha\beta )$ とおく. 直線 $\mathrm{AD},$ $\mathrm{BE},$ $\mathrm{CF}$ が平行であることを使って, $3$ 点 $\mathrm A',$ $\mathrm B',$ $\mathrm C'$ が同一直線上にあることを示せ.
解答例
- (1)
- $3$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C$ のうち $2$ 点以上が一致する場合は等式が明らかに成り立つから, $3$ 点が相異なる場合を考える.
このとき,
が成り立つ.$\mathrm A,\ \mathrm B,\ \mathrm C$ が同一直線上 $\iff \mathrm{arg}\dfrac{\gamma -\alpha}{\beta -\alpha} = n\pi$ ($n$: 整数) $\iff \dfrac{\gamma -\alpha}{\beta -\alpha}$ が実数 $\iff \overline{\left(\dfrac{\gamma -\alpha}{\beta -\alpha}\right)} = \dfrac{\gamma -\alpha}{\beta -\alpha}$ $\iff \dfrac{\bar\gamma -\bar\alpha}{\bar\beta -\bar\alpha} = \dfrac{\gamma -\alpha}{\beta -\alpha}$ $\iff (\beta -\alpha )(\bar\gamma -\bar\alpha )-(\bar\beta -\bar\alpha )(\gamma -\alpha ) = 0$ - (2)
- $\mathrm E(\beta -\alpha ),$ $\mathrm F(\delta -\gamma )$ とおくと, $\mathrm{AB} /\!/ \mathrm{OE},$ $\mathrm{CD} /\!/ \mathrm{OF}$ となるから,
が成り立つ. $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ が単位円周上にあるとき, $|\alpha | = 1$ つまり $\alpha\bar\alpha = |\alpha |^2 = 1$ から $\bar\alpha = \alpha ^{-1}$ であり, 同様に $\bar\beta = \beta ^{-1},$ $\bar\gamma = \gamma ^{-1},$ $\bar\delta = \delta ^{-1}$ であるから, \[\begin{aligned} &\mathrm{AB} /\!/ \mathrm{CD} \iff \frac{\delta ^{-1}-\gamma ^{-1}}{\beta ^{-1}-\alpha ^{-1}} = \frac{\delta -\gamma}{\beta -\alpha} \\ &\iff \frac{\gamma -\delta}{\alpha -\beta} = \frac{\gamma -\delta}{\alpha -\beta}\cdot\frac{\gamma\delta}{\alpha\beta} \iff 1 = \frac{\gamma\delta}{\alpha\beta} \\ &\iff \alpha\beta -\gamma\delta = 0 \end{aligned}\] が成り立つ.$\mathrm{AB} /\!/ \mathrm{CD}$ $\iff$ $\mathrm{OE},$ $\mathrm{OF}$ が同一直線上 $\iff \mathrm{arg}\dfrac{\delta -\gamma}{\beta -\alpha} = n\pi$ ($n$: 整数) $\iff \dfrac{\delta -\gamma}{\beta -\alpha}$ が実数 $\iff \overline{\left(\dfrac{\delta -\gamma}{\beta -\alpha}\right)} = \dfrac{\delta -\gamma}{\beta -\alpha}$ $\iff \dfrac{\bar\delta -\bar\gamma}{\bar\beta -\bar\alpha} = \dfrac{\delta -\gamma}{\beta -\alpha}$ - (3)
- こちらを参照.
- (4)
- ①
- $\mathrm B,$ $\mathrm A',$ $\mathrm C$ が同一直線上にあることから, (1) の結果により \[\begin{aligned} &(\alpha '-\beta )(\bar\gamma -\bar\beta )-(\overline{\alpha '}-\bar\beta )(\gamma -\beta ) = 0 \\ &\alpha '(\bar\gamma -\bar\beta )-\overline{\alpha '}(\gamma -\beta ) = \beta (\bar\gamma -\bar\beta )-\bar\beta (\gamma -\beta ) \end{aligned}\] が成り立つ. また, $\mathrm{PA}' \perp \mathrm{BC}$ から, (2) の結果により \[\begin{aligned} &(\alpha '-1)(\bar\gamma -\bar\beta )+(\overline{\alpha '}-1)(\gamma -\beta ) = 0 \\ &\alpha '(\bar\gamma -\bar\beta )+\overline{\alpha '}(\gamma -\beta ) = (\bar\gamma -\bar\beta )+(\gamma -\beta ) \end{aligned}\] が成り立つ. $2$ 式の辺々を加えて $\bar\gamma -\bar\beta $ で割ると, \[\begin{aligned} 2\alpha ' &= 1+\beta +(1-\bar\beta )\frac{\gamma -\beta}{\bar\gamma -\bar\beta} \\ &= 1+\beta +(1-\beta ^{-1})\frac{\gamma -\beta}{\gamma ^{-1}-\beta ^{-1}} \\ &= 1+\beta +(1-\beta ^{-1})\frac{-\beta\gamma (\beta -\gamma )}{\beta -\gamma} \\ &= 1+\beta +\gamma -\beta\gamma \end{aligned}\] が得られる. 同様に, $2\beta' = 1+\gamma +\alpha -\gamma\alpha,$ $2\gamma' = 1+\alpha +\beta -\alpha\beta$ である.
- ②
- $|\alpha | = |-\beta\gamma | = |\beta | = |-\gamma\alpha | = 1,$ $\alpha\cdot (-\beta\gamma )-\beta\cdot (-\gamma\alpha ) = 0$ であるから, (2) の結果により $\mathrm{AD} /\!/ \mathrm{BE}$ が成り立つ. よって, $\beta +\gamma\alpha = k(\alpha +\beta\gamma )$ なる実数 $k$ が存在する. 同様に, $\mathrm{AD} /\!/ \mathrm{CF}$ から, $\gamma +\alpha\beta = l(\alpha +\beta\gamma )$ なる実数 $l$ が存在する. よって, \[\begin{aligned} \frac{\gamma '-\alpha '}{\beta '-\alpha '} &= \frac{2\gamma '-2\alpha '}{2\beta '-2\alpha '} \\ &= \frac{(1+\alpha +\beta -\alpha\beta )-(1+\beta +\gamma -\beta\gamma )}{(1+\gamma +\alpha -\gamma\alpha )-(1+\beta +\gamma -\beta\gamma )} \\ &= \frac{(\alpha +\beta\gamma )-(\gamma +\alpha\beta )}{(\alpha +\beta\gamma )-(\beta +\gamma\alpha )} \\ &= \frac{(\alpha +\beta\gamma )-l(\alpha +\beta\gamma )}{(\alpha +\beta\gamma )-k(\alpha +\beta\gamma )} \\ &= \frac{1-l}{1-k} \end{aligned}\] は実数であるから, (1) の結果により $3$ 点 $\mathrm A'(\alpha '),$ $\mathrm B'(\beta '),$ $\mathrm C'(\gamma ')$ は同一直線上にある.
参考
- (4) の結果は「ウォレス=シムソンの定理」(Wallace–Simson theorem) または「シムソンの定理」として知られており, $3$ 点 $\mathrm A',$ $\mathrm B',$ $\mathrm C'$ を通る直線は $\triangle\mathrm{ABC}$ の「ウォレス=シムソン線」(Wallace–Simson line)または「シムソン線」と呼ばれる.
- 初等幾何学的な証明については, こちらを参照されたい.
問題《原点を通る直線に関する対称性》
複素数平面上の $2$ 点 $\mathrm P(z),$ $\mathrm P'(z')$ が原点 $\mathrm O$ と点 $\mathrm A(\alpha )$ を通る直線に関して対称であるためには,
$z'\bar\alpha = \bar z\alpha$ の成り立つことが必要十分であることを示せ.
解答例
$\alpha = r(\cos\theta +i\sin\theta )$ とおく.
$2$ 点 $\mathrm P(z),$ $\mathrm P'(z')$ を $\mathrm O$ を中心に $-\theta$ だけ回転移動した点を $\mathrm Q(w),$ $\mathrm Q'(w')$ とおく.
このとき,
\[\begin{aligned}
w &= z\{\cos (-\theta )+i\sin (-\sin\theta )\} \\
&= z(\cos\theta -i\sin\theta ), \\
\bar w &= \bar z\overline{(\cos\theta -i\sin\theta )} \\
&= \bar z(\cos\theta +i\sin\theta ) = \bar z\frac{\alpha}{r}, \\
w' &= z'(\cos\theta -i\sin\theta ) = z'\frac{\bar\alpha}{r}
\end{aligned}\]
が成り立つ.
よって,
が成り立つ.
| $2$ 点 $\mathrm P(z),$ $\mathrm P'(z')$ が直線 $\mathrm{OA}$ に関して対称 |
| $\iff$ $2$ 点 $\mathrm Q(w),$ $\mathrm Q'(w')$ が実軸に関して対称 |
| $\iff$ $w' = \bar w$ |
| $\iff$ $z'\dfrac{\bar\alpha}{r} = \bar z\dfrac{\alpha}{r}$ |
| $\iff$ $z'\bar\alpha = \bar z\alpha$ |
参考
$2$ 点 $\mathrm A(\alpha ),$ $\mathrm B(\beta )$ を通る直線 $\mathrm{AB}$ に関して点 $z$ と点 $w$ が対称であるとき,
\[ w = \frac{(\beta -\alpha )\bar z+\alpha\bar\beta -\bar\alpha\beta}{\bar\beta -\bar\alpha}\]
が成り立つ.
共円条件
問題《共円条件》
相異なる複素数 $\alpha,$ $\beta,$ $\gamma,$ $\delta$ で表される点が同一直線上にないとき,
$4$ 点がこの順に同一円周上に並ぶためには,
\[\frac{\alpha -\beta}{\gamma -\beta}\cdot\frac{\gamma -\delta}{\alpha -\delta}\]
が負の実数であることと同値であることを示せ.
解答例
$4$ 点 $\alpha,$ $\beta,$ $\gamma,$ $\delta$ がこの順に同一円周上に並ぶとする.
このとき, $\mathrm{arg}\,\dfrac{\alpha -\beta}{\gamma -\beta},$ $\mathrm{arg}\,\dfrac{\gamma -\delta}{\alpha -\delta}$ の符号は等しいから,
偏角を $-\pi$ より大, $\pi$ 以下の範囲で考えると, 円に内接する四角形の内角の和が $\pi$ であることから
\[\mathrm{arg}\,\frac{\alpha -\beta}{\gamma -\beta}\cdot\dfrac{\gamma -\delta}{\alpha -\delta} = \left|\mathrm{arg}\,\frac{\alpha -\beta}{\gamma -\beta}\right| +\left|\mathrm{arg}\,\frac{\gamma -\delta}{\alpha -\delta}\right| = \pi\]
が成り立つ.
これは, $\dfrac{\alpha -\beta}{\gamma -\beta}\cdot\dfrac{\gamma -\delta}{\alpha -\delta}$ が負の実数であることを意味している.
この逆も, 向かい合う内角の和が $\pi$ の四角形は円に内接することから従う.
この逆も, 向かい合う内角の和が $\pi$ の四角形は円に内接することから従う.
問題《トレミーの不等式と三角形のフェルマー点》
次の問いに答えよ.
ただし, 上の問題で示した「三角不等式」は証明なしに使ってよい.
- (1)
- $(b-a)(d-c)+(d-a)(c-b)$ を因数分解せよ.
- (2)
- 平面上の相異なる $4$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ に対して, 不等式 \[\mathrm{AB}\cdot\mathrm{CD}+\mathrm{AD}\cdot\mathrm{BC} \geqq \mathrm{AC}\cdot\mathrm{BD}\] が成り立つことを示せ. また, その等号成立条件を求めよ.
- (3)
- 最大の内角が $120^\circ$ 未満の $\triangle\mathrm{ABC}$ の内部に点 $\mathrm P$ をとり, $\triangle\mathrm{ABC}$ の外側に正三角形 $\mathrm{ABC}'$ をかく. $\mathrm{PA}+\mathrm{PB} \geqq \mathrm{PC}'$ が成り立つことを示せ. また, $\mathrm{PA}+\mathrm{PB}+\mathrm{PC}$ が最小になるとき, $\angle\mathrm{APB} = 120^\circ$ が成り立つことを示せ.
解答例
- (1)
- 与式を変形すると, \[\begin{aligned} &(b-a)(d-c)+(d-a)(c-b) \\ &= (bd-bc-ad+ac)+(cd-bd-ac+ab) \\ &= cd-bc-ad+ab \\ &= c(d-b)-a(d-b) \\ &= (c-a)(d-b) \end{aligned}\] となる.
- (2)
- $4$ 点 $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ に対応する複素数をそれぞれ $\alpha,$ $\beta,$ $\gamma,$ $\delta$ とおく. \[ (\beta -\alpha )(\delta -\gamma )+(\delta -\alpha )(\gamma -\beta ) = (\gamma -\alpha )(\delta -\beta )\] の両辺の絶対値をとると \[ |(\beta -\alpha )(\delta -\gamma )+(\delta -\alpha )(\gamma -\beta )| = |\gamma -\alpha ||\delta -\beta |\] となるから,「三角不等式」により \[\begin{aligned} |\beta -\alpha ||\delta -\gamma |+|\delta -\alpha ||\gamma -\beta | &\geqq |\gamma -\alpha ||\delta -\beta | \\ \mathrm{AB}\cdot\mathrm{CD}+\mathrm{AD}\cdot\mathrm{BC} &\geqq \mathrm{AC}\cdot\mathrm{BD} \end{aligned}\] となる. 等号成立は, 偏角を $-\pi$ より大, $\pi$ 以下の範囲で考えると, \[\begin{aligned} \mathrm{arg}\,(\beta -\alpha )(\delta -\gamma ) &= \mathrm{arg}\,(\delta -\alpha )(\gamma -\beta ) \\ \mathrm{arg}\,\dfrac{(\delta -\alpha )(\gamma -\beta )}{(\beta -\alpha )(\delta -\gamma )} &= 0 \\ \mathrm{arg}\,\frac{(\gamma -\beta )(\alpha -\delta )}{(\alpha -\beta )(\gamma -\delta )} &= \pi \\ \left|\mathrm{arg}\,\frac{\gamma -\beta}{\alpha -\beta}\right| +\left|\mathrm{arg}\,\frac{\alpha -\delta}{\gamma -\delta}\right| &= \pi \end{aligned}\] の場合, つまり $\mathrm A,$ $\mathrm B,$ $\mathrm C,$ $\mathrm D$ がこの順に同一円周上に並ぶ場合に限る.
- (3)
- (2) の結果により,
\[\mathrm{PA}\cdot\mathrm C'\mathrm B+\mathrm{PB}\cdot\mathrm{AC}' \geqq \mathrm P\mathrm C'\cdot\mathrm{AB}\]
が成り立つ.
$\triangle\mathrm{ABC}'$ は正三角形であることから, 両辺を $\mathrm C'\mathrm B = \mathrm{AC}' = \mathrm{AB}$ で割ると,
\[\mathrm{PA}+\mathrm{PB} \geqq \mathrm{PC}'\]
となる.
両辺に $\mathrm{PC}$ を加えると,「三角不等式」により,
\[\mathrm{PA}+\mathrm{PB}+\mathrm{PC} \geqq \mathrm{CP}+\mathrm{PC}' \geqq \mathrm{CC}' \]
が得られる.
等号成立は, $\mathrm P,$ $\mathrm A,$ $\mathrm C',$ $\mathrm B$ がこの順に同一円周上に並び, $\mathrm C,$ $\mathrm P,$ $\mathrm C'$ がこの順に同一直線上に並ぶ場合に限る.
このとき, 円に内接する四角形の性質から, \[\angle\mathrm{APB} = 180^\circ -\angle\mathrm{AC}'\mathrm B = 180^\circ -60^\circ = 120^\circ\] である.
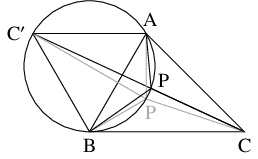
参考
- (2) で示した不等式は,「トレミーの不等式」(Ptolemy's inequality) と呼ばれ,「(第一) トレミーの定理」(こちらとこちらとこちらを参照) の一般化である.
- (3) と同様にして, $\mathrm{PA}+\mathrm{PB}+\mathrm{PC}$ が最小になるとき, \[\angle\mathrm{APB} = \angle\mathrm{BPC} = \angle\mathrm{CPA} = 120^\circ\] の成り立つことがわかる. このような点 $\mathrm P$ は $\triangle\mathrm{ABC}$ の「フェルマー点」または「トリチェリ点」(Fermat point, Torricelli point) などと呼ばれる (こちらを参照).
複素数と多角形
問題《三角形の相似条件》
複素数平面において,
が成り立つことを示せ.
ただし, 相似な $2$ つの三角形は, 対応する $3$ 頂点がどちらも時計回りに並んでいるか, どちらも反時計回りに並んでいるとき, 同じ向きであるという.
また, そうでないとき, 逆の向きであるという.
| $\triangle z_1z_2z_3,$ $\triangle w_1w_2w_3$ が同じ向きで相似 |
| $\iff$ $\dfrac{z_3-z_1}{z_2-z_1} = \dfrac{w_3-w_1}{w_2-w_1},$ |
| $\triangle z_1z_2z_3,$ $\triangle w_1w_2w_3$ が逆の向きで相似 |
| $\iff$ $\overline{\,\dfrac{z_3-z_1}{z_2-z_1}\,} = \dfrac{w_3-w_1}{w_2-w_1}$ |
解答例
三角形の相似条件「$2$ 組の辺の長さの比とその間の角が等しい」により,
が成り立つ.
| $\triangle z_1z_2z_3,$ $\triangle w_1w_2w_3$ が同じ向きで相似 |
| $\iff$ $\dfrac{|z_3-z_1|}{|z_2-z_1|} = \dfrac{|w_3-w_1|}{|w_2-w_1|},$ $\mathrm{arg}\,\dfrac{z_3-z_1}{z_2-z_1} = \mathrm{arg}\dfrac{w_3-w_1}{w_2-w_1}$ |
| $\iff$ $\left|\dfrac{z_3-z_1}{z_2-z_1}\right| = \left|\dfrac{w_3-w_1}{w_2-w_1}\right|,$ $\mathrm{arg}\,\dfrac{z_3-z_1}{z_2-z_1} = \mathrm{arg}\dfrac{w_3-w_1}{w_2-w_1}$ |
| $\iff$ $\dfrac{z_3-z_1}{z_2-z_1} = \dfrac{w_3-w_1}{w_2-w_1},$ |
| $\triangle z_1z_2z_3,$ $\triangle w_1w_2w_3$ が逆の向きで相似 |
| $\iff$ $\dfrac{|z_3-z_1|}{|z_2-z_1|} = \dfrac{|w_3-w_1|}{|w_2-w_1|},$ $-\mathrm{arg}\,\dfrac{z_3-z_1}{z_2-z_1} = \mathrm{arg}\dfrac{w_3-w_1}{w_2-w_1}$ |
| $\iff$ $\left|\dfrac{z_3-z_1}{z_2-z_1}\right| = \left|\dfrac{w_3-w_1}{w_2-w_1}\right|,$ $-\mathrm{arg}\,\dfrac{z_3-z_1}{z_2-z_1} = \mathrm{arg}\dfrac{w_3-w_1}{w_2-w_1}$ |
| $\iff$ $\left|\overline{\,\dfrac{z_3-z_1}{z_2-z_1}\,}\right| = \left|\dfrac{w_3-w_1}{w_2-w_1}\right|,$ $\mathrm{arg}\,\overline{\,\dfrac{z_3-z_1}{z_2-z_1}\,} = \mathrm{arg}\dfrac{w_3-w_1}{w_2-w_1}$ |
| $\iff$ $\overline{\,\dfrac{z_3-z_1}{z_2-z_1}\,} = \dfrac{w_3-w_1}{w_2-w_1}$ |
問題《座標法》
複素数 $z$ の虚部を $\mathrm{Im}\,(z)$ で表す.
$n$ 角形 $z_1z_2\cdots z_n$ の面積 $S$ は
\[ S = \displaystyle\frac{1}{2}\left|\sum_{k = 1}^n\mathrm{Im}\,(\overline{z_k}z_{k+1})\right|\]
であり, 絶対値記号の中は頂点の並び方が反時計回りのとき正, 時計回りのとき負であることを示せ.
ただし, $z_{n+1} = z_1$ とする.
(参考: $2000$ 横浜市立大)
解答例
- (I)
- $n = 3$ のとき.
- (i)
- $z_3 = 0$ のとき. $\theta = \mathrm{arg}\,\dfrac{z_2}{z_1}$ $(-\pi < \theta < \pi,$ $\theta \neq 0)$ とおく. $\cos\theta +i\sin\theta = \dfrac{|z_1|}{|z_2|}\cdot\dfrac{z_2}{z_1}$ であるから, $\mathrm{Im}\,(z) = \dfrac{z-\overline{z}}{2i}$ により \[\begin{aligned} \sin\theta &= \frac{|z_1|}{|z_2|}\mathrm{Im}\left(\frac{z_2}{z_1}\right) = \frac{|z_1|}{|z_2|}\cdot\frac{1}{2i}\left(\frac{z_2}{z_1}-\frac{\overline{z_2}}{\overline{z_1}}\right) \\ &= \frac{|z_1|}{|z_2|}\cdot\frac{1}{2i}\cdot\frac{\overline{z_1}z_2-z_1\overline{z_2}}{|z_1|^2} = \frac{1}{|z_1||z_2|}\mathrm{Im}\,(\overline{z_1}z_2) \end{aligned}\] が成り立つ. よって, \[ S = \frac{1}{2}|z_1||z_2|\left|\sin\theta\right| = \frac{1}{2}|\mathrm{Im}\,(\overline{z_1}z_2)|\] が成り立つ. $\mathrm{Im}\,(\overline{z_1}z_2)$ の符号は, $\sin\theta$ の符号, つまり $\theta = \mathrm{arg}\,\dfrac{z_2}{z_1}$ の符号と一致する.
- (ii)
- 一般の場合. 平行移動しても面積は変わらないから, (i) において $z_1,$ $z_2,$ $z_3$ を $w_1 = z_1-z_3,$ $w_2 = z_2-z_3,$ $0$ に置き換えると, $\mathrm{Im}\,(z+w) = \mathrm{Im}\,(z)+\mathrm{Im}\,(w),$ $\mathrm{Im}\,(\overline{z}) = -\mathrm{Im}\,(z)$ により \[\begin{aligned} S &= \frac{1}{2}|\mathrm{Im}\,(\overline{w_1}w_2)| = \frac{1}{2}\left|\mathrm{Im}\,((\overline{z_1}-\overline{z_3})(z_2-z_3))\right| \\ &= \frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_2-z_2\overline{z_3}-z_3\overline{z_1}+|z_3|^2)\right| \\ &= \frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_2)-\mathrm{Im}\,(z_2\overline{z_3})-\mathrm{Im}\,(z_3\overline{z_1})\right| \\ &= \frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_2)+\mathrm{Im}\,(\overline{z_2}z_3)+\mathrm{Im}\,(\overline{z_3}z_1)\right| \end{aligned}\] が得られる. 絶対値記号の中は, $\mathrm{arg}\,\dfrac{w_2}{w_1} = \mathrm{arg}\,\dfrac{z_2-z_3}{z_1-z_3}$ と符号が一致するから, 頂点の並び方が反時計回りのとき正, 時計回りのとき負である.
- (II)
- $n = m-1$ ($m$: $4$ 以上の整数) のとき公式が成り立つとし, $n = m$ の場合を考える.
$m-1$ 角形 $\mathrm P_1\cdots\mathrm P_{m-1}$ の面積を $S'$ とおく.
- 点 $\mathrm P_m$ が $m-1$ 角形 $\mathrm P_1\cdots\mathrm P_{m-1}$ の外部にあるとき. \[\begin{aligned} S &= S'+\triangle\mathrm P_1\mathrm P_{m-1}\mathrm P_m \\ &= \frac{1}{2}\left|\sum_{k = 1}^{m-2}\mathrm{Im}\,(\overline{z_k}z_{k+1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)\right| \\ &\qquad +\frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_{m-1})+\mathrm{Im}\,(\overline{z_{m-1}}z_m)+\mathrm{Im}\,(\overline{z_m}z_1)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^{m-2}\mathrm{Im}\,(\overline{z_k}z_{k+1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)+\mathrm{Im}\,(\overline{z_1}z_{m-1})\right. \\ &\qquad \left.+\mathrm{Im}\,(\overline{z_{m-1}}z_m)+\mathrm{Im}\,(\overline{z_m}z_1)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^m\mathrm{Im}\,(\overline{z_k}z_{k+1})\right| \end{aligned}\] が成り立つ.
- 点 $\mathrm P_m$ が $m-1$ 角形 $\mathrm P_1\cdots\mathrm P_{m-1}$ の内部にあるとき. この $m-1$ 角形と $\triangle\mathrm P_1\mathrm P_m\mathrm P_{m-1}$ の頂点の並び方は同じであるから, \[\begin{aligned} S &= S'-\triangle\mathrm P_1\mathrm P_m\mathrm P_{m-1} \\ &= \frac{1}{2}\left|\sum_{k = 1}^{m-2}\mathrm{Im}\,(\overline{z_k}z_{k+1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)\right| \\ &\qquad -\frac{1}{2}\left|\mathrm{Im}\,(\overline{z_1}z_m)+\mathrm{Im}\,(\overline{z_m}z_{m-1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^{m-2}\mathrm{Im}\,(\overline{z_k}z_{k+1})+\mathrm{Im}\,(\overline{z_{m-1}}z_1)-\mathrm{Im}\,(\overline{z_1}z_m)\right. \\ &\qquad \left.-\mathrm{Im}\,(\overline{z_m}z_{m-1})-\mathrm{Im}\,(\overline{z_{m-1}}z_1)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^m\mathrm{Im}\,(\overline{z_k}z_{k+1})\right| \end{aligned}\] が成り立つ.
参考
- $z_1 = a+bi,$ $z_2 = c+di$ ($a,$ $b,$ $c,$ $d$: 実数) とすると, \[\overline{z_1}z_2 = (a-bi)(c+di) = (ac+bd)+(ad-bc)i\] から, \[\triangle 0z_1z_2 = \frac{1}{2}|\mathrm{Im}(\overline{z_1}z_2)| = \frac{1}{2}|ad-bc|\] が得られる.
- 複素数 $z_1 = x_1+y_1i,$ $\cdots,$ $z_n = x_n+y_ni$ ($n \geqq 3,$ $x_k,$ $y_k$: 実数) に対して, $n$ 角形 $z_1z_2\cdots z_n$ の面積 $S$ は, $z_{n+1} = z_1$ とおくと, \[\begin{aligned} S &= \frac{1}{2}\left|\mathrm{Im}\left(\sum_{k = 1}^n\overline{z_k}z_{k+1}\right)\right| = \frac{1}{2}\left|\sum_{k = 1}^n\mathrm{Im}(\overline{z_k}z_{k+1})\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^n\mathrm{Im}(x_k-y_ki)(x_{k+1}+y_{k+1}i)\right| \\ &= \frac{1}{2}\left|\sum_{k = 1}^n(x_ky_{k+1}-y_kx_{k+1})\right| \end{aligned}\] と表される. この公式は「座標法」と呼ばれ, 測量でよく利用されている.
