点と直線の距離
点と直線の距離
定理《点と直線の距離》
点 $(x_0,y_0)$ と直線 $ax+by+c = 0$ の距離 $d$ は
\[ d = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\]
である.
証明
問題《平行な $2$ 直線間の距離》
- (1)
- $m,$ $n_1,$ $n_2$ を実数とし, $m \neq 0$ とする. 互いに平行な $2$ 直線 $y = mx+n_1,$ $y = mx+n_2$ の間の距離を求めよ.
- (2)
- $a,$ $b,$ $c_1,$ $c_2$ を実数とし, $(a,b) \neq (0,0)$ とする. 互いに平行な $2$ 直線 $ax+by+c_1 = 0,$ $ax+by+c_2 = 0$ の間の距離を求めよ.
解答例
- (1)
- 求める距離は, $2$ 直線 $y = mx+n_1$ の $y$ 切片 $(0,n_1)$ と直線 $mx-y+n_2 = 0$ の距離に等しいから, \[\frac{|m\cdot 0+(-1)\cdot n_1+n_2|}{\sqrt{m^2+(-1)^2}} = \frac{|n_2-n_1|}{\sqrt{m^2+1}}\] である.
- (2)
- (i)
- $b \neq 0$ のとき. $2$ 直線の方程式は $y = -\dfrac{a}{b}x-\dfrac{c_1}{b},$ $y = -\dfrac{a}{b}x-\dfrac{c_2}{b}$ と変形できるから, (1) によりその間の距離は \[\frac{\left| -\dfrac{c_2}{b}+\dfrac{c_1}{b}\right|}{\sqrt{\left( -\dfrac{a}{b}\right) ^2+1}} = \frac{|c_1-c_2|}{\sqrt{a^2+b^2}} \quad \cdots [1]\] である.
- (ii)
- $b = 0$ のとき. $2$ 直線の方程式は $x = -\dfrac{c_1}{a},$ $x = -\dfrac{c_2}{a}$ と変形できるから, その間の距離は \[\left| -\frac{c_2}{a}+\frac{c_1}{a}\right| = \frac{|c_1-c_2|}{|a|}\] である. これは $[1]$ に $b = 0$ を代入した値に等しい.
問題《三角形の面積の公式とその応用》
次のことを示せ.
- (1)
- 原点 $\mathrm O$ と点 $\mathrm P(a,b),$ $\mathrm Q(c,d)$ を頂点とする三角形 $\mathrm{OPQ}$ の面積は \[\triangle\mathrm{OPQ} = \frac{1}{2}|ad-bc|\] である.
- (2)
- 各頂点の $x$ 座標, $y$ 座標が整数であるような正三角形は存在しない.
解答例
- (1)
- 辺 $\mathrm{OP}$ の長さは $\sqrt{a^2+b^2}$ である. また, 直線 $\mathrm{OP}:bx-ay = 0$ と点 $\mathrm Q(c,d)$ の距離 $d$ は \[ d = \frac{|bc-ad|}{\sqrt{b^2+(-a)^2}} = \frac{|ad-bc|}{\sqrt{a^2+b^2}}\] であるから, \[\begin{aligned} \triangle\mathrm{OPQ} &= \frac{1}{2}\mathrm{OP}\cdot d \\ &= \frac{1}{2}\sqrt{a^2+b^2}\cdot\frac{|ad-bc|}{\sqrt{a^2+b^2}} \\ &= \frac{1}{2}|ad-bc| \quad \cdots [1] \end{aligned}\] が成り立つ.
- (2)
- 各頂点の $x$ 座標, $y$ 座標が整数である正三角形 $\mathrm{OPQ}$ の存在を仮定する.
平行移動で面積は変わらないことから $\mathrm O$ が原点であるとしても一般性を失わないので, その場合を考える.
$\mathrm P(a,b),$ $\mathrm Q(c,d)$ とおく.
このとき, $[1]$ が成り立つ.
また, $\triangle\mathrm{OPQ}$ が正三角形であることから,
\[\triangle\mathrm{OPQ} = \frac{1}{2}\mathrm{OP}^2\sin 60^\circ = \frac{\sqrt 3}{4}(a^2+b^2) \quad \cdots [2]\]
が得られる.
よって, $[1],$ $[2]$ から,
\[\sqrt 3 = \frac{2|ad-bc|}{a^2+b^2}\]
が成り立つ.
$a,$ $b,$ $c,$ $d$ は整数であることから右辺は有理数であるが, これは $\sqrt 3$ が無理数であることに反する.
ゆえに, 各頂点の $x$ 座標, $y$ 座標が整数であるような正三角形は存在しない.
参考
問題《角の二等分線の傾き》
$a,$ $b$ を $b \neq \pm a$ なる実数とする.
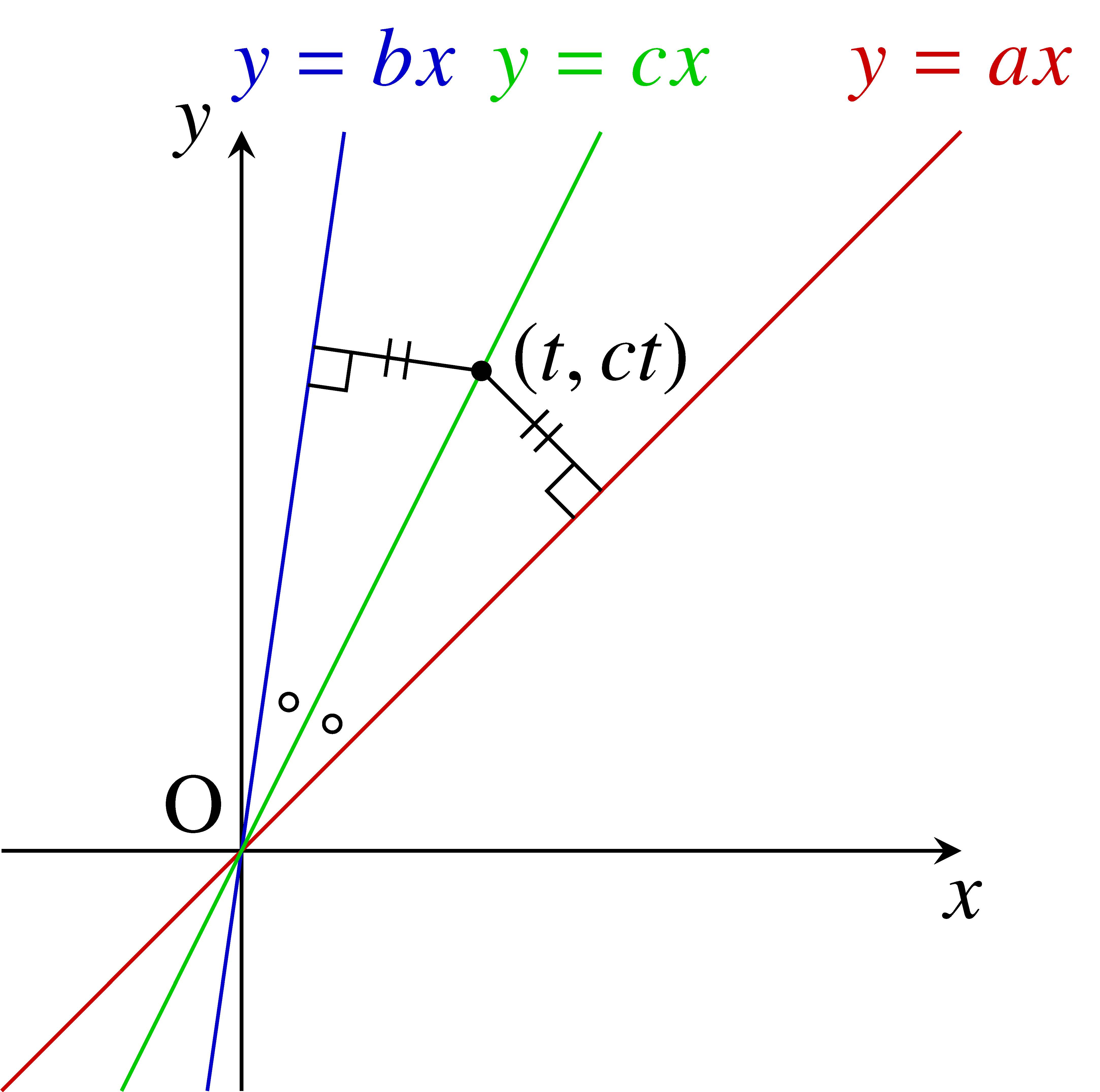
$2$ 直線 $y = ax,$ $y = bx$ のなす角の二等分線の傾き $c$ を $a,$ $b$ で表す公式を, 点と直線の距離の公式から導け.
解答例
角の二等分線 $y = cx$ 上の点 $(t,ct)$ $(t \neq 0)$ と $2$ 直線 $ax-y = 0,$ $bx-y = 0$ の距離は等しいから,
\[\begin{aligned}
\frac{|at-ct|}{\sqrt{a^2+(-1)^2}} &= \frac{|bt-ct|}{\sqrt{b^2+(-1)^2}} \\
|a-c|\sqrt{b^2+1} &= |b-c|\sqrt{a^2+1}
\end{aligned}\]
が成り立つ.
 両辺を $2$ 乗すると
\[ (a-c)^2(b^2+1) = (b-c)^2(a^2+1)\]
よって
\[\begin{aligned}
(a^2+1)(c-b)^2-(b^2+1)(c-a)^2 &= 0 \\
\{ (a^2+1)-(b^2+1)\} c^2-2\{ (a^2+1)b-(b^2+1)a\} c \quad & \\
+(a^2+1)b^2-(b^2+1)a^2 &= 0 \\
(a+b)(a-b)c^2-2(a-b)(ab-1)c-(a+b)(a-b) &= 0 \\
(a+b)c^2-2(ab-1)c-(a+b) &= 0
\end{aligned}\]
となるから, $2$ 次方程式の解の公式により
\[\begin{aligned}
c &= \frac{ab-1\pm\sqrt{(ab-1)^2+(a+b)^2}}{a+b} \\
&= \frac{ab-1\pm\sqrt{(a^2+1)(b^2+1)}}{a+b}
\end{aligned}\]
が得られる.
両辺を $2$ 乗すると
\[ (a-c)^2(b^2+1) = (b-c)^2(a^2+1)\]
よって
\[\begin{aligned}
(a^2+1)(c-b)^2-(b^2+1)(c-a)^2 &= 0 \\
\{ (a^2+1)-(b^2+1)\} c^2-2\{ (a^2+1)b-(b^2+1)a\} c \quad & \\
+(a^2+1)b^2-(b^2+1)a^2 &= 0 \\
(a+b)(a-b)c^2-2(a-b)(ab-1)c-(a+b)(a-b) &= 0 \\
(a+b)c^2-2(ab-1)c-(a+b) &= 0
\end{aligned}\]
となるから, $2$ 次方程式の解の公式により
\[\begin{aligned}
c &= \frac{ab-1\pm\sqrt{(ab-1)^2+(a+b)^2}}{a+b} \\
&= \frac{ab-1\pm\sqrt{(a^2+1)(b^2+1)}}{a+b}
\end{aligned}\]
が得られる.

