線形漸化式
線形漸化式
定義《線形漸化式》
$r$ を正の整数とする.
の形の数列 $\{ a_n\}$ の漸化式を (定数係数) $r+1$ 項間「線形漸化式」(linear recurrence relation) と呼ぶ.
| $a_{n+r} = p_0a_n+\cdots +p_{r-1}a_{n+r-1}+q$ ($p_k,$ $q$: 定数) |
$2$ 項間線形漸化式 (定数係数)
定理《定数係数 $2$ 項間線形漸化式》
$p,$ $q$ ($p \neq 0,$ $1$) を定数とする.
$a_1$ の値と
\[ a_{n+1} = pa_n+q \quad \cdots [\spadesuit ]\]
で定まる数列 $\{ a_n\}$ について, $1$ 次方程式
\[ x = px+q \quad \cdots [\spadesuit ]'\]
の解を $\alpha$ とおく.
このとき, $\{ a_n-\alpha\}$ は初項 $a_1-\alpha,$ 公比 $p$ の等比数列であり, $\{ a_n\}$ の一般項は
\[ a_n = (a_1-\alpha )p^{n-1}-\alpha\]
である.
証明
$[\spadesuit ],$ $[\spadesuit ]'$ の辺々を引くと,
\[ a_{n+1}-\alpha = p(a_n-\alpha )\]
となる.
これは, $\{ a_n-\alpha\}$ が初項 $a_1-\alpha,$ 公比 $p$ の等比数列であることを表している.
よって,
\[ a_n-\alpha = (a_1-\alpha )p^{n-1}\]
から, 求める等式が得られる.
別証明
$[\spadesuit ]$ において $n$ を $n+1$ に置き換えると,
\[ a_{n+2} = pa_{n+1}+q\]
となる.
この式から $[\spadesuit ]$ を引くと,
\[ a_{n+2}-a_{n+1} = p(a_{n+1}-a_n)\]
が得られるので, $\{ a_{n+1}-a_n\}$ は初項 $a_2-a_1,$ 公比 $p$ の等比数列である.
\[\frac{a_2-a_1}{p-1} = \frac{pa_1+q-a_1}{p-1} = a_1-\frac{q}{p-1} = a_1-\alpha\]
であるから, $n \geqq 2$ のとき,
\[\begin{aligned}
a_n &= a_1+\sum_{k = 1}^{n-1}(a_2-a_1)p^{k-1} \\
&= a_1+\frac{a_2-a_1}{p-1}(p^{n-1}-1) \\
&= a_1+(a_1-\alpha )(p^{n-1}-1) \\
&= (a_1-\alpha )p^{n-1}-\alpha,
\end{aligned}\]
つまり $a_n-\alpha = (a_1-\alpha )p^{n-1}$ が成り立つ.
これは $n = 1$ のときも成り立つから, $\{ a_n-\alpha\}$ は初項 $a_1-\alpha,$ 公比 $p$ の等比数列である.
参考
$p,$ $q,$ $r$ $(p,\ r \neq 0)$ を定数とする.
$a_1$ の値と
\[ a_{n+1} = pra_n+qr^{n+1}\]
で定まる数列 $\{ a_n\}$ について, 数列 $\left\{\dfrac{a_n}{r^n}\right\}$ は両辺を $r^{n+1}\,(\neq 0)$ で割って得られる漸化式
\[\frac{a_{n+1}}{r^{n+1}} = p\frac{a_n}{r^n}+q\]
を満たすから, $1$ 次方程式 $x = px+q$ の解を $\alpha$ とおくとき, $\{ a_n\}$ の一般項は
\[ a_n = r^n\{ (a_1-\alpha )p^{n-1}-\alpha\}\]
である.
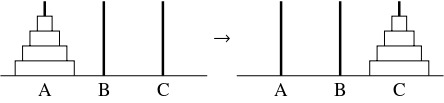
問題《ハノイの塔》
地面に $3$ 本の棒が立てられており,
そのうちの $1$ 本に穴の開いた半径の異なる円盤が半径の大きい順に通されている.
$1$ 本の棒の最も上にある $1$ 枚を別の棒の最も上に移す操作を $1$ 手と数え,
$1$ 本の棒の最も上にある $n$ 枚を別の棒の最も上に移すときの手数の最小値を $a_n$ とおく.
ただし, いずれの段階においても小さい円盤の上に大きい円盤は置かないものとする.
- (1)
- すべての正の整数 $n$ に対して $a_{n+1} = 2a_n+1$ であることを説明せよ.
- (2)
- 数列 $\{ a_n\}$ の一般項を求めよ.

解答例
- (1)
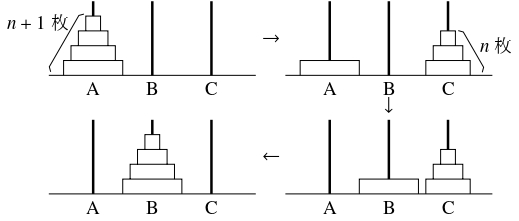
- 最初に円盤を通された棒を A とし, 残りの棒を B, C とする.
棒 A の最も上にある $n+1$ 枚を棒 B の最も上に移すためには,
まず上の $n$ 枚を棒 C に移し, 次に棒 A に残された $1$ 枚を棒 B に移し, 最後に棒 C に移された $n$ 枚を棒 B に移す必要がある.
ゆえに,
\[ a_{n+1} = a_n+1+a_n = 2a_n+1 \quad \cdots [1]\]
が成り立つ.
- (2)
- \[ \alpha = 2\alpha +1 \quad \cdots [2]\] を解くと $\alpha = -1$ となるので, $[1]-[2]$ から \[\begin{aligned} a_{n+1}-\alpha &= 2(a_n-\alpha ) \\ a_{n+1}+1 &= 2(a_n+1) \end{aligned}\] となる. $\{ a_n+1\}$ は初項 $a_1+1 = 1+1 = 2,$ 公比 $2$ の等比数列であるから, \[\begin{aligned} a_n+1 &= 2^n \\ a_n &= 2^n-1 \end{aligned}\] である.
参考
本問は, フランスの数学者 E・リュカによって考案された「ハノイの塔」(tower of Hanoi) と呼ばれるパズルの手数の最小値を求める問題である.
$n+1$ 枚の場合に全体を $n$ 枚のかたまりと $1$ 枚に分けて考えると $n$ 枚の場合が現れ, $a_n,$ $a_{n+1}$ の関係式が得られた.
この方法は, 漸化式を立てて場合の数を求める問題の定石の $1$ つと言える.
$2$ 項間線形漸化式 (非定数係数)
以下では, 係数が $n$ の関数であるような $2$ 項間漸化式の問題を扱う.
問題《中心付き多角数の一般項》
$p$ を $3$ 以上の整数とする.
\[ a_1 = 1, \quad a_{n+1} = a_n+pn\]
で定まる数列 $\{ a_n\}$ の一般項を求めよ.
解答例
$n \geqq 2$ のとき,
\[\begin{aligned}
a_n &= a_1+\sum_{k = 1}^{n-1}(a_{k+1}-a_k) \\
&= a_1+\sum_{k = 1}^{n-1}pk \\
&= 1+p\sum_{k = 1}^{n-1}k \\
&= 1+\frac{p(n-1)n}{2} \quad \cdots [1]
\end{aligned}\]
である.
これは $n = 1$ のときも成り立つから, $\{ a_n\}$ の一般項は $[1]$ である.
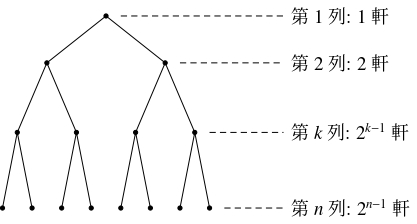
問題《二分木の巡回セールスマン問題》
家が $n$ 本の列上に並んでおり, 第 $k$ 列 $(1 \leqq k \leqq n)$ には $2^{k-1}$ 軒の家がある.
各家は, 次の列の $2$ 軒の家とそれぞれ $1$ 本の道で, 前の列の $1$ 軒の家と $1$ 本の道で結ばれている.
これらの他に道はなく, すべての道の長さは $1$ である.
$1$ 人のセールスマンが第 $1$ 列の家を出発して第 $n$ 列までのすべての家を最短で歩いて周り, 出発点に戻る.
- (A)
- セールスマンが歩く道のりを $a_n$ とおく.
- (1)
- $a_{n+1} = a_n+2^{n+1}$ が成り立つことを説明せよ.
- (2)
- 数列 $\{ a_n\}$ の一般項を求めよ.
- (B)
- セールスマンが通り得る経路の総数を求めよ.

(参考: 慶應義塾大)
解答例
- (A)
- (1)
- セールスマンはすべての道を往復し, $n+1$ 列の家が増えると道は $2^n$ 本だけ増えるから, \[ a_{n+1} = a_n+2^{n+1}\] が成り立つ.
- (2)
- $n \geqq 2$ のとき, \[\begin{aligned} a_n &= a_1+\sum_{k = 1}^{n-1}(a_{k+1}-a_k) = 0+\sum_{k = 1}^{n-1}2^{k+1} \\ &= \frac{4(2^{n-1}-1)}{2-1} = 2^{n+1}-4 \quad \cdots [1] \end{aligned}\] である. これは $n = 1$ のときも成り立つから, $\{ a_n\}$ の一般項は $[1]$ である.
- (B)
- $1 \leqq k \leqq n-1$ なる各整数 $k$ に対して第 $k$ 列の家と第 $k+1$ 列の家を行き来する方法は $2^{2^{k-1}}$ 通りあるから, セールスマンが通りうる経路の総数は \[\begin{aligned} 2^1\cdots 2^{2^{k-1}}\cdots 2^{2^{n-2}} &= 2^{1+\cdots +2^{k-1}+\cdots +2^{n-2}} \\ &= 2^{1\cdot (2^{n-1}-1)/(2-1)} = 2^{2^{n-1}-1} \end{aligned}\] である.
参考
点の集合と各 $2$ 点間の移動コスト (距離など) が与えられたとき, すべての点をちょうど $1$ 回ずつ巡って出発点に戻る経路のうち, 総移動コストが最小の経路を求める問題を「巡回セールスマン問題」(traveling salesman problem) と呼ぶ.
「計算複雑性理論」では, 一般的な状況下での「計算量」が議論の対象になる.
$3$ 項間線形漸化式 (定数係数)
定理《定数係数 $3$ 項間線形漸化式》
$p,$ $q$ $(q \neq 0)$ を定数とする.
$a_1,$ $a_2$ の値と
\[ a_{n+2}+pa_{n+1}+qa_n = 0 \quad \cdots [\heartsuit ]\]
で定まる数列 $\{ a_n\}$ について, $2$ 次方程式
\[ x^2+px+q = 0 \quad \cdots [\heartsuit ]'\]
の $2$ つの解を $\alpha,$ $\beta$ とおく.
このとき, $\{ a_n\}$ の一般項は,
\[ a_n = \begin{cases}
\dfrac{a_2-\beta a_1}{\alpha -\beta}\alpha ^{n-1}-\dfrac{a_2-\alpha a_1}{\alpha -\beta}\beta ^{n-1} & (\alpha \neq \beta ), \\
a_1\alpha ^{n-1}+(a_2-\alpha a_1)(n-1)\alpha ^{n-2} & (\alpha = \beta )
\end{cases}\]
である.
証明
解と係数の関係により
\[\alpha +\beta = -p, \quad \alpha\beta = q\]
であるから,
\[\begin{aligned}
[\heartsuit ] &\iff a_{n+2}-(\alpha +\beta )a_{n+1}+\alpha\beta a_n = 0 \\
&\iff \left\{\begin{array}{l}
a_{n+2}-\alpha a_{n+1} = \beta (a_{n+1}-\alpha a_n) \quad \cdots [1], \\
a_{n+2}-\beta a_{n+1} = \alpha (a_{n+1}-\beta a_n) \quad \cdots [2]
\end{array}\right.
\end{aligned}\]
が成り立つ.
- (i)
- $\alpha \neq \beta$ のとき. $[1],$ $[2]$ は, それぞれ $\{ a_{n+1}-\alpha a_n\}$ が初項 $a_2-\alpha a_1,$ 公比 $\beta$ の等比数列であること, $\{ a_{n+1}-\beta a_n\}$ が初項 $a_2-\beta a_1,$ 公比 $\alpha$ の等比数列であることを意味するから, \[\begin{aligned} a_{n+1}-\alpha a_n &= (a_2-\alpha a_1)\beta ^{n-1} \quad \cdots [3], \\ a_{n+1}-\beta a_n &= (a_2-\beta a_1)\alpha ^{n-1} \quad \cdots [4] \end{aligned}\] が得られる. $([4]-[3])\div (\beta -\alpha )$ から, 求める等式が得られる.
- (ii)
- $\alpha = \beta$ のとき. $[1]$ は, $\{ a_{n+1}-\alpha a_n\}$ が初項 $a_2-\alpha a_1,$ 公比 $\alpha$ の等比数列であることを意味するから, \[ a_{n+1}-\alpha a_n = (a_2-\alpha a_1)\alpha ^{n-1}\] が成り立つ. $q \neq 0$ から $\alpha \neq 0$ であることに注意して, 両辺を $\alpha ^{n+1}$ で割ると, \[\frac{a_{n+1}}{\alpha ^{n+1}}-\frac{a_n}{\alpha ^n} = \frac{a_2-\alpha a_1}{\alpha ^2}\] となる. よって, $\left\{\dfrac{a_n}{\alpha ^n}\right\}$ は初項 $\dfrac{a_1}{\alpha},$ 公差 $\dfrac{a_2-\alpha a_1}{\alpha ^2}$ の等差数列であるから, \[\begin{aligned} \frac{a_n}{\alpha ^n} &= \frac{a_1}{\alpha}+(n-1)\frac{a_2-\alpha a_1}{\alpha ^2} \\ a_n &= a_1\alpha ^{n-1}+(a_2-\alpha a_1)(n-1)\alpha ^{n-2} \end{aligned}\] が成り立つ.
参考
$p,$ $q,$ $r$ $(q \neq 0)$ を定数として, $a_1,$ $a_2$ の値と
\[ a_{n+2}+pa_{n+1}+qa_n+r = 0\]
で定まる数列 $\{ a_n\}$ は
\[ (a_{n+3}-a_{n+2})+p(a_{n+2}-a_{n+1})+q(a_{n+1}-a_n) = 0\]
を満たすから, $\{ a_n\}$ の一般項は上記の方法で求められる.
問題《フィボナッチ数列の一般項と和》
$1$ 歩目は $1$ 段だけ上るとし, $2$ 歩目以降は $1$ 歩で $1$ 段上ることも $2$ 段上ることもできるとして, $n$ 段の階段を上る方法の総数を $F_n$ とおく.
また, 同様の方法で $n$ 段以下の階段を上る方法の総数を $S_n$ とおく.
- (1)
- $F_{n+2} = F_n+F_{n+1}$ が成り立つことを示せ.
- (2)
- 数列 $\{ F_{n+1}-\alpha F_n\},$ $\{ F_{n+1}-\beta F_n\}$ がそれぞれ公比 $\beta,$ $\alpha$ の等比数列になるような定数 $\alpha,$ $\beta$ $(\alpha > \beta )$ を $1$ 組求めよ.
- (3)
- 数列 $\{ F_n\}$ の一般項を求めよ.
- (4)
- 数列 $\{ S_n\}$ の一般項を求めよ.
(参考: $2022$ 山口大, $2021$ 浜松医科大, $2020$ 大分大ほか)
解答例
- (1)
- $n+2$ 段の階段を上るとき, 最後の $1$ 歩に着目すると, 次の $2$ つの場合が考えられる.
- (i)
- 最後の $1$ 歩で $2$ 段上る場合. $n+2$ 段を上る方法は, $n$ 段の上り方 $F_n$ 通りだけある.
- (ii)
- 最後の $1$ 歩で $1$ 段上る場合. $n+2$ 段を上る方法は, $n+1$ 段の上り方 $F_{n+1}$ 通りだけある.
- (2)
- 数列 $\{ F_{n+1}-\alpha F_n\},$ $\{ F_{n+1}-\beta F_n\}$ がそれぞれ公比 $\beta,$ $\alpha$ の等比数列であるとき, \[\begin{aligned} F_{n+2}-\alpha F_{n+1} &= \beta (F_{n+1}-\alpha F_n), \\ F_{n+2}-\beta F_{n+1} &= \alpha (F_{n+1}-\beta F_n) \end{aligned}\] から \[ F_{n+2} = (\alpha +\beta )F_{n+1}-\alpha\beta F_n \quad \cdots [2]\] が成り立つ. $[1],$ $[2]$ から, \[\alpha +\beta = 1,\quad \alpha\beta = -1\] が成り立てばよい. このとき, $\alpha,$ $\beta$ は $2$ 次方程式 $x^2-x-1 = 0$ の解であるから, 条件を満たす $\alpha,$ $\beta$ の組として \[ (\alpha,\beta ) = \left(\frac{1+\sqrt 5}{2},\frac{1-\sqrt 5}{2}\right)\] がとれる.
- (3)
- $1$ 歩目は $1$ 段だけ上るという条件から $F_1 = F_2 = 1$ である. よって, 数列 $\{ F_{n+1}-\alpha F_n\},$ $\{ F_{n+1}-\beta F_n\}$ の初項は, それぞれ \[\begin{aligned} F_2-\alpha F_1 = 1-\alpha &= \frac{1-\sqrt 5}{2} = \beta, \\ F_2-\beta F_1 = 1-\beta &= \frac{1+\sqrt 5}{2} = \alpha \end{aligned}\] である. したがって, $\alpha,$ $\beta$ のとり方から, \[\begin{aligned} F_{n+1}-\alpha F_n &= \beta ^n, \\ F_{n+1}-\beta F_n &= \alpha ^n \end{aligned}\] が成り立つ. 辺々を引くと \[ (\alpha -\beta )F_n = \alpha ^n-\beta ^n\] となるので, $\alpha -\beta = \sqrt 5$ から \[ F_n = \frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^n-\left(\frac{1-\sqrt 5}{2}\right) ^n\right\}\] が成り立つ.
- (4)
- $S_n = F_1+\cdots +F_n$ であるから, \[ F_k = -F_{k+1}+F_{k+2} \quad (1 \leqq k \leqq n)\] の辺々を加えると \[\begin{aligned} S_n &= (-F_2+F_3)+\cdots +(-F_{n+1}+F_{n+2}) \\ &= -F_2+F_{n+2} \\ &= F_{n+2}-1 \\ &= \frac{1}{\sqrt 5}\left\{\left(\frac{1+\sqrt 5}{2}\right) ^{n+2}-\left(\frac{1-\sqrt 5}{2}\right) ^{n+2}\right\}-1 \end{aligned}\] が得られる.
参考
- 初期条件 $F_1 = F_2 = 1$ と漸化式 $F_{n+2} = F_n+F_{n+1}$ で定まる数列 \[\{ F_n\}:1,1,2,3,5,8,13,21,34,55,89,144,\cdots\] を「フィボナッチ数列」(Fibonacci sequence) と呼ぶ. この数列の項は「フィボナッチ数」と呼ばれ, 花びらの枚数, 植物の種が並んでできるらせんの本数など, 自然界でよく見られる整数である.「フィボナッチ数列」は, 次の問題でも登場する: 先頭は動かないように, $2$ 番目以降は動かないか隣に移るように, $1$ 列に並んだ $n$ 人を並べ替える方法の総数は $F_n$ である.
- (3) の公式は「ビネの公式」(Binet's formula) として知られている.
- $n$ 番目の「フィボナッチ数」$F_n$ は $\dfrac{1}{\sqrt 5}\left(\dfrac{1+\sqrt 5}{2}\right) ^n+\dfrac{1}{2}$ の整数部分に等しい (参考: 鳴門教育大). 実際,「ビネの公式」 \[ F_n = \frac{\alpha ^n-\beta ^n}{\sqrt 5}\] と $-1 < \beta < 0,$ $\sqrt 5 > 2$ により \[\left| F_n-\frac{\alpha ^n}{\sqrt 5}\right| = \left| -\frac{\beta ^n}{\sqrt 5}\right| = \frac{|\beta |^n}{\sqrt 5} < \frac{1}{2}\] であるから, \[\begin{aligned} -\frac{1}{2} &< F_n-\frac{\alpha ^n}{\sqrt 5} < \frac{1}{2} \\ \left(\frac{\alpha ^n}{\sqrt 5}+\frac{1}{2}\right) -1 = \frac{\alpha ^n}{\sqrt 5}-\frac{1}{2} &< F_n < \frac{\alpha ^n}{\sqrt 5}+\frac{1}{2} \end{aligned}\] が成り立つ. $F_n$ は整数であるから, これは $\dfrac{\alpha ^n}{\sqrt 5}+\dfrac{1}{2}$ の整数部分が $F_n$ に等しいことを意味する.
- 「フィボナッチ数列」の隣り合う項の比は「黄金比」$1:\dfrac{1+\sqrt 5}{2}$ に限りなく近づいていくこともよく知られている (こちらを参照).
