関数の増減・曲線の凹凸 (理系)
関数の増減
定理《関数の増減と導関数の符号》
区間 $I$ で微分可能な関数 $f(x)$ に対して,
- (1)
- $I$ において $f'(x) \geqq 0$ $\Longrightarrow$ $f(x)$ は $I$ において単調増加
- (2)
- $I$ において $f'(x) \leqq 0$ $\Longrightarrow$ $f(x)$ は $I$ において単調減少
証明
- (1)
- $I$ において $f'(x) \geqq 0$ が成り立つとする. $x_1,$ $x_2 \in I,$ $x_1 < x_2$ のとき, $x_1 < x < x_2$ なる実数 $x$ をとると, 平均値の定理により, $x_1 < c_1 < x < c_2 < x_2$ なるある実数 $c_1,$ $c_2$ に対して \[\begin{aligned} f(x)-f(x_1) &= f'(c_1)(x-x_1) \geqq 0, \\ f(x_2)-f(x) &= f'(c_2)(x_2-x) \geqq 0 \end{aligned}\] となるから, $f(x_1) \leqq f(x) \leqq f(x_2)$ が成り立つ. ゆえに, $f(x)$ は $I$ において単調増加である.
- (2)
- (1) と同様である.
問題《$x \to \infty$ のとき $f(x) \to \infty$ となる条件》
$\varepsilon$ を正の数とする.
実数 $a$ を含む開区間 $(a-\varepsilon,\infty )$ において, 関数 $f(x)$ が微分可能であり, $2$ 次導関数をもつとする.
このとき,
- (i)
- $f'(a) > 0$
- (ii)
- $f''(x) > 0 \quad (x \geqq a)$
- (iii)
- $\lim\limits_{x \to \infty}f(x) = \infty$
- (1)
- (i), (ii) が成り立つならば, (iii) が成り立つことを示せ.
- (2)
- (ii) のみでは (iii) は成り立たない. その例を挙げよ.
(参考: 津田塾大)
解答例
- (1)
- (i), (ii) を仮定する. $x > a$ なる各実数 $x$ に対して, $f(x)$ は閉区間 $[a,x]$ において連続で, 解区間 $(a,x)$ において微分可能であるから, 平均理の定理により, \[\frac{f(x)-f(a)}{x-a} = f'(c)\] つまり \[ f(x) = f(a)+(x-a)f'(c)\] を満たす実数 $c$ が $a < c < x$ の範囲に存在する. (ii) から $f'(x)$ は $x \geqq a$ において単調増加であるので, このとき \[ f'(c) > f'(a)\] であり, \[ f(x) > f(a)+(x-a)f'(a) \quad \cdots [1]\] が成り立つ. さらに, (i) から $f'(a) > 0$ であるので, \[\lim\limits_{x \to \infty}(x-a)f'(a) = \infty \quad \cdots [2]\] が成り立つ. ゆえに, $[1]$, $[2]$ から, $\lim\limits_{x \to \infty}f(x) = \infty$ が成り立つ.
- (2)
- $f(x) = e^{-x}$ として, $a$ を任意の実数とすると, \[ f'(x) = -e^{-x}, \quad f''(x) = e^{-x} > 0\ (x \geqq a)\] となって (ii) が成り立つが, $\lim\limits_{x \to \infty}f(x) = 0$ となり, (iii) は成り立たない.
参考
$2$ 回微分可能な関数 $f(x)$ に対して, 次のことが成り立つ.
- 開区間 $(l,\infty )$ において, 曲線 $y = f(x)$ が下に凸 (resp. 上に凸) で, 接線の傾きが正 (resp. 負) であるならば, $\lim\limits_{x \to \infty}f(x) = \infty$ (resp. $\lim\limits_{x \to \infty}f(x) = -\infty$) が成り立つ.
- 開区間 $(-\infty,r)$ において, 曲線 $y = f(x)$ が下に凸 (resp. 上に凸) で, 接線の傾きが負 (resp. 正) であるならば, $\lim\limits_{x \to -\infty}f(x) = \infty$ (resp. $\lim\limits_{x \to -\infty}f(x) = -\infty$) が成り立つ.
曲線の凹凸
問題《アネェージの曲線の形状》
$a > 0$ とする.
$xy$ 平面において, 原点 $\mathrm O$ と円周
\[ x^2+\left( y-\frac{a}{2}\right)^2 = \frac{a^2}{4}\]
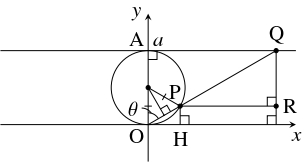
上の点 $\mathrm P$ を通る直線, 直線 $y = a$ の交点を $\mathrm Q$ とおく.
さらに, 点 $\mathrm P$ を通って $x$ 軸に平行な直線, 点 $\mathrm Q$ を通って $y$ 軸に平行な直線の交点を $\mathrm R$ とおく.
点 $\mathrm P$ がこの円周の点 $\mathrm O$ を除く部分を動くとき, 点 $\mathrm R$ が描く曲線を $C$ とおく.
- (1)
- $\mathrm A(0,a)$ とおき, $\mathrm{OA}$ を始線, 時計回りを正の向きとして動径 $\mathrm{OP}$ の表す角を $\theta$ とおく. $\theta$ を用いた $C$ の媒介変数表示を求めよ.
- (2)
- $y = f(x)$ の形の $C$ の方程式を導け.
- (3)
- $C$ の凹凸を調べ, その概形を描け.
解答例
- (1)
- (i)
- 点 $\mathrm P$ が第 $1$ 象限にあるとき. 点 $\mathrm R$ の $x$ 座標は, 点 $\mathrm Q$ の $x$ 座標に等しいから, 直角三角形 $\mathrm{OAQ}$ に着目すると, \[ x = \mathrm{AQ} = a\tan\theta\] が得られる. また, 点 $\mathrm R$ の $y$ 座標は, 点 $\mathrm P$ の $y$ 座標に等しいから, \[\mathrm{OP} = 2\cdot\frac{a}{2}\cos\theta = a\cos\theta\] (等辺の長さが $\dfrac{a}{2},$ 底角の大きさが $\theta$ の二等辺三角形の底辺の長さ) であることに注意して, 点 $\mathrm P$ から $x$ 軸に下ろした垂線の足 $\mathrm H$ を頂点とする直角三角形 $\mathrm{OHP}$ に着目すると, \[ y = \mathrm{HP} = \mathrm{OP}\cos\theta = a\cos ^2\theta\] 得られる. よって, 点 $\mathrm R$ の座標は \[ (a\tan\theta,a\cos ^2\theta ) \quad \cdots [1]\] で表される.
- (ii)
- 点 $\mathrm P$ が第 $2$ 象限にあるとき. 円の対称性により曲線 $C$ も $y$ 軸に関して対称であるから, 点 $\mathrm R$ の座標は $[1]$ で表される.
- (iii)
- $\mathrm P = \mathrm A$ のとき. 点 $\mathrm R$ の座標 $(0,a)$ は $[1]$ で表される.
- (2)
- $\cos ^2\theta = \dfrac{1}{1+\tan ^2\theta}$ に $\cos ^2\theta = \dfrac{y}{a},$ $\tan\theta = \dfrac{x}{a}$ を代入すると, 求める $C$ の方程式
$\dfrac{y}{a} = \dfrac{1}{1+\dfrac{x^2}{a^2}}$ つまり $y = \dfrac{a^3}{a^2+x^2}$が得られる.
- (3)
- $x$ の関数 $y = \dfrac{a^3}{a^2+x^2}$ について,
\[\begin{aligned}
y' &= -\frac{2a^3x}{(a^2+x^2)^2}, \\
y'' &= -2a^3\cdot\frac{1\cdot (a^2+x^2)^2-x\cdot 2(a^2+x^2)\cdot 2x}{(a^2+x^2)^4} \\
&= \frac{2a^3(3x^2-a^2)}{(a^2+x^2)^3}
\end{aligned}\]
であるから,
\[\begin{aligned}
y' \geqq 0 &\iff x \leqq 0, \\
y' \leqq 0 &\iff x \geqq 0, \\
y'' \geqq 0 &\iff x \leqq -\frac{a}{\sqrt 3},\ \frac{a}{\sqrt 3} \leqq x, \\
y'' \leqq 0 &\iff -\frac{a}{\sqrt 3} \leqq x \leqq \frac{a}{\sqrt 3}
\end{aligned}\]
が成り立つ.
よって, 曲線 $C$ の凹凸は次の表のようになる.
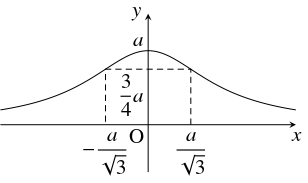
さらに, \[\lim\limits_{x \to \pm\infty}\frac{a^3}{a^2+x^2} = 0\] であるから, 曲線 $C$ の概形は次のようになる.
$x$ $\cdots$ $-\dfrac{a}{\sqrt 3}$ $\cdots$ $0$ $\cdots$ $\dfrac{a}{\sqrt 3}$ $\cdots$ $y'$ $+$ $+$ $+$ $0$ $-$ $-$ $-$ $y''$ $+$ $0$ $-$ $-$ $-$ $0$ $+$ $y$ 
変曲点
$\dfrac{3}{4}a$
極大
$a$
変曲点
$\dfrac{3}{4}a$
参考
- 本問の曲線は,「アネェージの曲線」または「アネェージの魔女」(witch of Agnesi) として知られている. 「魔女」は, 縄を意味するイタリア語の versiera の誤訳である. アネェージは, 女性で史上 $2$ 人目の大学教授となったイタリアの数学者であり, 初の微分積分学の教科書を著したことで有名である.
- 「アネェージの曲線」とその漸近線が囲む図形の面積は, もとになる円の面積の $4$ 倍である (こちらを参照).
問題《凸関数のグラフの接線》
実数値関数 $f(x)$ が点 $x = a$ を含む開区間 $I$ で $2$ 回微分可能であるとし, 曲線 $y = f(x)$ の点 $(a,f(a))$ における接線を $y = g(x)$ とする.
このとき, 区間 $I$ において
\[ f''(x) \leqq 0 \Longrightarrow f(x) \leqq g(x)\]
が成り立つことを示せ.
解答例
$h(x) = g(x)-f(x)$ とおく.
このとき,
\[ g(x) = f'(a)(x-a)+f(a)\]
であるから,
\[ h'(x) = f'(a)-f'(x) = -\{ f'(x)-f'(a)\}, \quad h(a) = 0\]
となる.
よって, 区間 $I$ において,
が成り立つ.
| $f''(x) \leqq 0$ $\iff f'(x)$ は単調減少 |
| $\iff \begin{cases} h'(x) \geqq 0 & (x \leqq a), \\ h'(x) \leqq 0 & (x \geqq a) \end{cases}$ |
| $\iff$ $h(x)$ は $x = a$ で極小かつ最小の値をとる |
| $\Longrightarrow h(x) \geqq h(a)$ $\iff$ $h(x) \geqq 0$ |
| $\iff f(x) \leqq g(x)$ |
参考
本問で示した関数の性質は,「上に凸」(convex upward) である関数の特徴付けを与える (「凸関数」については, こちらを参照).
問題《関数のグラフの複接線と変曲点の個数》
関数 $f(x)$ は $2$ 回微分可能, $f''(x)$ は連続であり, 曲線 $C:y = f(x)$ は線分である部分をもたないとする.
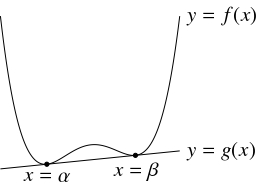
$C$ に相異なる $2$ 点 $(\alpha,f(\alpha )),$ $(\beta,f(\beta ))$ $(\alpha < \beta )$ で接する直線が存在するためには, $C$ が $\alpha < x < \beta$ の範囲に少なくとも $2$ つの変曲点をもつことが必要であることを示せ.
解答例
曲線 $C$ に $2$ 点 $(\alpha,f(\alpha )),$ $(\beta,f(\beta ))$ $(\alpha < \beta )$ で接する直線の存在を仮定する.
このとき,
\[\frac{f(\beta )-f(\alpha )}{\beta -\alpha} = f'(\alpha ) = f'(\beta )\]
が成り立つ.
また, 平均値の定理により
\[\frac{f(\beta )-f(\alpha )}{\beta -\alpha} = f'(\gamma ), \quad \alpha < \gamma < \beta\]
を満たす実数 $\gamma$ が存在する.
$C$ が線分である部分をもたないという仮定から, $(\alpha,\gamma ),$ $(\gamma,\beta )$ の各区間において, 常に $f''(x) = 0$ となることはない.
さらに, $f'(\alpha ) = f'(\gamma ) = f'(\beta )$ と $f''(x)$ の連続性により, これらの各区間において, $f''(x) > 0$ となる $x$ があれば $f''(x) < 0$ となる $x$ があり, $f''(x) < 0$ となる $x$ があれば $f''(x) > 0$ となる $x$ がある.
よって, ある実数 $x_1,$ $x_2$ $(\alpha < x_1 < \gamma < x_2 < \beta )$ の前後で, それぞれ $f''(x)$ の符号が変化する.
ゆえに, $y = f(x)$ は少なくとも $2$ つの変曲点 $(x_1,f(x_1)),$ $(x_2,f(x_2))$ をもつ.
問題《$4$ 次関数のグラフの複接線の傾き》
$4$ 次関数 $f(x),$ $1$ 次関数 $g(x),$ 相異なる実数 $\alpha,$ $\beta$ について,
曲線 $C:y = f(x),$ 直線 $l:y = g(x)$ が直線 $x = \alpha,$ $x = \beta$ 上でそれぞれ接するとする.
このとき, $C$ の接線 $l$ の傾き $m$ は $f'''(x) = 0$ の解 $\gamma$ を用いて
\[ m = f'(\gamma )\]
と表されることを示せ.
$f(x)-g(x)$ が $(x-\alpha )^2,$ $(x-\beta )^2$ で割り切れることは証明なしに使ってよい (こちらを参照).
解答例
$f(x)-g(x) = a(x-\alpha )^2(x-\beta )^2,$ $g(x) = mx+n$ ($a,$ $m,$ $n$: 実数, $a,$ $m \neq 0$) とおく.
このとき,
\[\begin{aligned}
f(x) &= a(x-\alpha )^2(x-\beta )^2+mx+n, \\
f'(x) &= a\{ 2(x-\alpha )\cdot (x-\beta )^2+(x-\alpha )^2\cdot 2(x-\beta )\} +m \\
&= 2a(x-\alpha )(x-\beta )(2x-\alpha -\beta )+m, \\
f''(x) &= 2a\{ 1\cdot (x-\beta )\cdot (2x-\alpha -\beta ) \\
&\qquad +(x-\alpha )\cdot 1\cdot (2x-\alpha -\beta ) \\
&\qquad +(x-\alpha )\cdot (x-\beta )\cdot 2\} \\
&= 2a\{ 6x^2-6(\alpha +\beta )x+\alpha ^2+4\alpha\beta +\beta ^2\}, \\
f'''(x) &= 12a(2x-\alpha -\beta )
\end{aligned}\]
であるから, $f'''(x) = 0$ の解 $\gamma$ は
\[\gamma = \dfrac{\alpha +\beta}{2}\]
であり,
\[ f'(\gamma ) = 2a(\gamma -\alpha )(\gamma -\beta )(2\gamma -\alpha -\beta )+m = m\]
が成り立つ.
ゆえに, $C$ の接線 $l$ の傾きは $m = f'(\gamma )$ と表される.
別解
$h(x) = f(x)-g(x) = a(x-\alpha )^2(x-\beta )^2,$ $g(x) = mx+n$ ($a,$ $m,$ $n$: 実数, $a,$ $m \neq 0$) とおく.
このとき,
\[\begin{aligned}
h'(x) &= a\{ 2(x-\alpha )\cdot (x-\beta )^2+(x-\alpha )^2\cdot 2(x-\beta )\} \\
&= 2a(x-\alpha )(x-\beta )(2x-\alpha -\beta )
\end{aligned}\]
から, $\gamma = \dfrac{\alpha +\beta}{2}$ は $h'(\gamma ) = 0$ を満たす.
\[ h'(\alpha ) = h'(\gamma ) = h'(\beta ) = 0, \quad \alpha < \gamma < \beta\]
であるから, $3$ 次関数 $y = h'(x)$ のグラフの対称性により $(\gamma,h'(\gamma ))$ は $y = h'(x)$ のただ $1$ つの変曲点である.
よって, $\gamma$ は $h'''(\gamma ) = 0$ を満たし, また $g'(x) = m,$ $g''(x) = g'''(x) = 0$ であるから
\[ f'''(\gamma ) = g'''(\gamma )+h'''(\gamma ) = 0\]
であり,
\[ f'(\gamma ) = g'(\gamma )+h'(\gamma ) = m\]
が成り立つ.
参考
曲線 $C$ と直線 $l$ が相異なる $2$ 点で接するとき, $l$ を $C$ の「複接線」(double tangent line) と呼ぶ.

※$2022/06/16$『接線・法線 (理系)』から移動
